Concours kiné Berck : 9 années de QCM Lentilles. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

On peut modéliser une loupe par une lentille mince convergente. Une personne désire voir 5 fois plus grand les caractères d'un livre. La vergence de la lentille est C=7 d. Déterminer à quelle distance ( en cm) le lecteur doit placer sa loupe.(2,8 ; 11,4 ; 14,2 ; 17,8 ; 21,2 ; aucune réponse exacte) Toutes les grandeurs sont algébriques l'image est virtuelle et le grandissement vaut donc +5 = OA'/OA soit OA'=5 OA relation de conjugaison : 7 =1/OA'-1/OA soit 7=1/(5OA)-1/OA 7= -4 /(5OA) ; OA= -4/ (7*5)= -0,114 m = -11,4 cm. distance loupe-journal : 11,4 cm. Un objet AB de hauteur 3 cm est placé devant une lentille convergente de vergence 10 d. L'objet, assimilable à un segment est perpendiculaire à l'axe optique principal de la lentille. A est situé sur l'axe optique, à 30 cm du centre optique O de la lentille. Combien y a-t-il d'affirmations exactes ? - Le foyer image F ' se trouve à 40 cm de A ( vrai) - Le foyer image est le point où tous les rayons qui sortent de la lentille convergent. ( faux) - L'image A'B' est de même sens que AB ( faux) - La taille de l'image A'B' est de 2 cm ( faux) - L'image se trouve à 5 cm du foyer objet ( faux)     On appelle pouvoir séparateur de l'oeil la plus petite distance angulaire entre deux points séparés par l'oeil. Pour un oeil normal, cette distance angulaire vaut : e= 3 10-4 rad. On veut observer deux cratères lunaires avec une lunette astronomique. Distance des cratères : 30 km ; Distance terre-lune = 3,8 105 km. Déterminer le grossissement minimal de la lunette pour pouvoir distinguer les deux cratères. (2 ; 4 ; 6 ; 8 ; 10 ; aucune réponse exacte) Diamètre apparent des " deux cratères " = 30 / 3,8 105 = 7,9 10-5 rad, valeur inférieure à e. Grossissement minimum de la lunette : 3 10-4 / 7,9 10-5 = 3,8 ( soit 4)     Web www.chimix.com Une lentille convergente de distance focale f' = 25 cm donne d'un objet réel A, situé sur l'axe optique à 105 cm devant le foyer principal objet une image A'. Calculer la distance (en cm) qui sépare A' du foyer principal image. (6,0 ; 8,0 ; 12 ; 16 ; 18 ; aucune réponse exacte) Formule de conjugaison ( les distances algébriques sont écrites en bleu et en gras) 1/f' = 1/OA' - 1/OA avec OA = -(1,05+0,25 )=-1,3 m ; 1/f' = 1/0,25 = 4 d ; 1/OA' = 4+1/(-1,3) = 3,2 ; OA' = 0,31 m ; F'A' = 0,31-0,25 = 0,06 m = 6 cm. Texte : un objet de hauteur 3,0 cm est placé devant une lentille convergente de vergence C. Cet objet se situe à 10 cm devant le foyer principal objet F de la lentille. L'objet assimilable à un segment est perpendiculaire à l'axe de la lentille et le point A est sur l'axe optique. 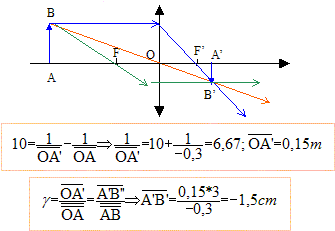La lentille donne de cet objet une image inversée, réelle, de hauteur 4,5 cm. Analyse : Question relative à la vergence( d) C. (5,0 ; 6,7 ; 8,9 ; 10 ; 12 ; aucune réponse exacte) Grandissement transversal négatif ( image renversée par rapport à l'objet) g = - A'B'/AB = - 4,5 / 3 ; g = -1,5. Les grandeurs algébriques sont écrites en gras et en bleu. Or g = OA'/OA ; OA' = -1,5 OA. De plus OA = OF+FA = -f' - 0,1. Par suite OA' = 1,5(f'+0,1) Ecrire la formule de conjugaison : 1/f' = 1/OA' - 1/OA. 1/f' = 1/[1,5(f'+0,1)] + 1/(f'+0,1) 1/f' =2,5 / [1,5(f'+0,1)] ; 1,5(f'+0,1) = 2,5 f' ; 0,15 = f' ; C= 1/f' = 1/0,15 ; C = 6,7 d.

retour -menu