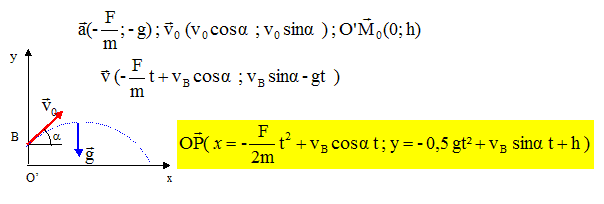Concours kiné berck : 9 années de QCM Projectile, chute. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Un projectile est lancé dans le champ de pesanteur avec une vitesse v0 faisant un angle a avec l'horizontale. On néglige l'action de l'air sur le projectile. Le sommet S de la trajectoire a pour coordonnées ( xS= 10 m ; yS=7m). Quelle est la valeur de l'angle de tir a. (en °). tan a = 2yS/xS =2*7/10 = 1,4 ; a = 54,5°. Quelle est la valeur de la vitesse v0 en m/s ? v02 = 2gyS/sin2a ; v0=[2gyS]½/sin a =[2*9,8*7]½ / sin 54,5 =14,4 m/s. On considère un projectile lancé à partir d'un point A avec une vitesse initiale v0 faisant un angle a avec l'horizontale. Soit S le sommet de la trajectoire. On néglige l'action de l'air sur le projectile. Parmi les affirmations suivantes lesquelles sont exactes ? Le vecteur vitesse en S est nul. Faux.· Au sommet la composante verticale de la vitesse est nulle. Le vecteur vitesse en S est horizontal. Vrai.· La vitesse en S est minimale. Vrai. La coordonnée du vecteur vitesse en S suivant l'axe Ox est nulle. Faux.· La coordonnée du vecteur vitesse en S suivant l'axe Oy est nulle. Vrai. ·   Un hélicoptère volant horizontalement à une altitude de 123 m avec une vitesse de 350 km/h laisse tomber une caisse que l'on considérera comme ponctuelle, en passant à la verticale d'un point H du sol. On néglige l'action de l'air. A quelle distance (en m) du point H va se produire l'impact ? v0=350/3,6 =97,2 m/s ; 0=-0,5*9,8 x2/97,22 +123 x2 = 123*97,22/4,9 ; x = (123/4,9)½ *97,2 =487 m. Une bille d'acier sphérique de rayon r= 4 cm tombe verticalement dans l'air à vitesse constante V. L'air exerce sur la bille une force de frottement fluide qui a pour expression F=Kpr² rair V² où K est une constante. On négligera la poussée d'Archimède s'exerçant sur la bille. rair = 1,29 kg/m3 ; racier = 7800 kg/m3 ; K=0,2. Déterminer l'énergie cinétique (J) de la bille en arrivant au sol. La vitesse limite de chute est atteinte : valeur de la vitesse constante, donc mouvement uniforme ; de plus le mouvement est rectiligne. Le principe d'inertie ( 1ère loi de Newton) indique que la somme des forces appliquée s à la bille est nulle. valeur du poids =valeur des frottements soit mg = Kpr²rair V² avec m (kg ) =masse volumique acier fois volume de la bille (m3) m= racier 4pr3/3 racier 4pr3/3 g= Kpr²rair V² d'où V² = 4rracier g / (3Krair) V² = 4* 4 10-3 *7800*9,8 / (3*0,2*1,29) = 1580,16 m²/s² masse de la bille = racier 4pr3/3 = 7800*4*3,14*(4 10-3)3/3 = 2,09 10-3 kg énergie cinétique = ½mV² = 0,5 *2,09 10-3 *1580,16 = 1,651 J.     Web www.chimix.com Lors d’un match de volley en plain air, un volleyeur de l’équipe bleue au service frappe à la volée un ballon de masse M=0,5 kg situé à une hauteur h=2 m au dessus du sol avec une vitesse initiale v0=10 m/s sous un angle de 45°. Un des joueurs de l’équipe rouge, positionné à x0=15 mètres du premier joueur, souhaite intercepter le ballon lorsque celui-ci est à une hauteur H=3,5 m et commence à courir vers le filet à une vitesse V. Il y a un vent de force constante F=1 N qui s’exerce parallèlement au sol sur le ballon et le freine, celui-ci étant à une hauteur H=3,5 m. cos 30 = 0,8 ; sin 30 = 0,5 ; 30½~5,5 ; g = 10 m/s2. Les équations horaires du ballon s'écrivent. Vrai. xb(t) =v0 cos a t-½F/m t2 ; yb(t) =h+v0 sin a t-½g t2. Le joueur de l’équipe rouge a un mouvement xj(t) = x0-vj xt. Vrai. Il tape sur le ballon à la hauteur H à l’instant t= 15 s en xb=7 m. Faux. yb= -5 t2 + 10*0,7 t +2. 3,5=-5t2 +7t +2 ; 5t2 -7t +1,5=0 ; t2 -1,4 t +0,3=0 D½ =0,87 ; t1= 1,14 s ; t2 = 0,27 s. Abscisses du ballon : x=-1/(2*0,5) t2+10*0,7 t =- t2+7 t ; x1 = 6,7 m ; x2 = 1,8 m. Sa vitesse pour réussir à taper sur le ballon à la hauteur H est environ 8 m/s. Vrai. xj(t) = x0-vj xt ; vj x= (15-xj)/t ; v1 =(15-6,7)/1,14 = 7,3 m/s ; v2 =(15-1,8)/0,27 = 50 m/s (impossible). Une petite bille de forme parfaitement sphérique de rayon 5 mm et de masse volumique r= 2,0 103 kg/m3, tombe au centre d'un tuyau cylindrique de rayon 50 cm remplie d'eau. La bille est initialement à 1 m au dessus de la surface de l'eau. On néglige les frottements de l'air. L'origine des temps est prise à l'instant du contact avec l'eau. Le niveau de référence pour l'énergie potentielle est la surface de l'eau. On prendra g = 10 N/kg ; p~3 ; 20½~4,5. L'énergie potentielle de pesanteur initiale de la bille est 1 J. Faux. Volume de la bille V=4/3pr3~4*(5 10-3)3=5 10-7 m3. Masse de la bille : m = rV=2 103*5 10-7 =10-3 kg. Energie potentielle initiale Ep =mgh = 10-3*10*1 = 0,01 J. La vitesse de la bille à l'instant où elle touche l'eau est de l’ordre de 10 m/s. Faux. La bille est en chute libre : on choisit un axe vertical orienté vers le bas dont l'origine est la position initiale de la bille. z=½gt2 ; z=5t2 ; v=gt = 10 t soit v2 = 2gh = 20 : v~4,5 m/s. L'énergie cinétique perdue par la bille au cours du choc est transférée au milieu liquide. On observe des ondes progressives transversales à la surface de l'eau se propageant dans toutes les directions à partir du point d'impact. L'onde touche le bord de la cuvette à l'instant t=0,1 seconde. La célérité des ondes à la surface de l'eau est de 5 m.s-1. Vrai. 0,5 m parcouru en 0,1 s : c= 0,5/0,1 = 5 m/s. La célérité de l'onde est modifiée si la goutte tombait de 50 cm de haut au lieu de 1 m. Faux. L'énergie transmise au milieu liquide serait plus petite. La vitesse dépend des caractéristiques du milieu de propagation de l'onde. A un instant pris comme origine des temps on lance vertcalement vers le haut un projectile d'un point situé à 8,0 m au dessus d'une rivière. Le projectile entre en contact avec l'eau de la rivière 1,9 s plus tard. On néglige l'action de l'air. Calculer la valeur de la vitesse ( en km/h) avec laquelle on a lancé le projectile. (11 ; 18 ; 21 ; 25 ; 27 ; aucune bonne réponse) On choisi un axe vertical, orienté vers le bas ; l'origine est le point de lancement : z = ½gt² -v0t = 4,9 t² -v0t au contact de la rivière z = 8 et t = 1,9 d'où : 8 = 4,9*1,9²-1,9 v0 ; v0= 5,1 m/s ; soit 5,1*3,6 = 18 km/h. 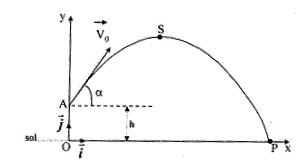On lance un projectile considéré comme ponctuel, à partir d'un point A avec une vitesse initiale v0 faisant un angle a avec l'horizontale. On néglige l'action de l'air sur le projectile. h = 2,0 m ; yS=3,4 m ; xP=8,2 m. Calculer a (°). 12 ; 27 ; 32 ; 41 ; 59 ; aucune réponse exacte. équations horaires : x = v0cos a t ; y = -½gt2 +v0sin a t + h vitesse : vx=v0cos a ; vy=-gt +v0sin a en S : vy S=0 soit t = v0sin a / g ; repport dans y : yS =(v0sin a)2/ (2g) + h 3,4 = (v0sin a)2/ 19,62 +2 ; v0sin a = 5,24. trajectoire : y = -½g x2 / (v0cos a)2 + x tan a + h en P : 0 = -½*9,81* 8,22 / (v0cos a)2 + 8,2 tan a + 2 -329,8 / (v0cos a)2+ 8,2 tan a + 2 =0 ; remplacer v0 par 5,24 / sina d'où : -12 tan2 a + 8,2 tan a + 2 =0 ; -12X2 +8,2X+2=0 avec X = tan a la résolution donne : tan a =0,874 soit a = 41° En déduire la valeur de v0(m/s). 4,0 ; 8,0 ; 16 ; 24 ; 32 ; aucune réponse exacte) v0 = 5,24 / sin a =5,24 / sin 41 = 8,0 m/s.

retour -menu