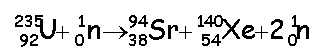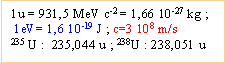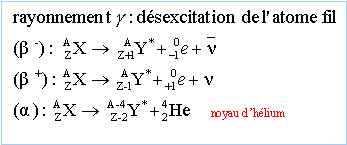Concours kiné berck : 9 annnées de QCM radioactivité. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Le réacteur d'un sous marin nucléaire fonctionne avec de l'uranium enrichi en isotope fissile Z=92 A=235 . Les noyaux d'uranium 235 subissent différentes fissions parmi lesquelles l'une des plus fréquente est la suivante : U =234,9942 u ; Sr=93,9154 u ; Xe=139,9252 u ; neutron : 1,0087 u ; 1u=1,6606 10-27 kg =931,5 MeV/c² 1eV=1,602 10-19C Calculer l'énergie libérée (en MeV) par cette réaction. perte de masse : |Dm| = | 139,9252 + 93,9154+1,0087-234,9942 |= 0,1449 u Energie libérée : 0,1449* 931,5 = 135 MeV. On suppose que toute les fissions sont identiques à la précédente . On suppose que le rendement de la transformation de l'énergie nucléaire en énergie électrique est de 30%. Calculer la masse d'uranium 235 (en kg) consommée en 200 j par le sous-marin dont le réacteur a une puissance de 30 MW. Puissance thermique : 30 106 / 0,3 = 108 W = 100 M W. Durée en seconde : 200*24*3600 = 1,728 107 s Energie thermique (J) = puissance (W) fois durée (s) =108*1,728 107 =1,728 1015 J. Energie libérée par une fission : 135 106 * 1,6 10-19 =2,16 10-11 J Energie libérée par une mole d'uranium 235 : 2,16 10-11 *6,02 1023= 1,3 1013 J. Quantité de matière (mol) d'uranium 235 : n=1,728 1015 / 1,3 1013 = 132,9 mol Masse molaire de l'uranium 235 : M=235 g/mol. Masse d'uranium consommé : nM=132,9*235 = 31,2 kg. La masse atomique de l'uranium naturel est égale à 238,029 u (unité de masse atomique). Quel est le pourcentage d'uranium 235 contenu dans l'uranium naturel ? x =0,022 / 3,007 = 7,3 10-3 ( 0,73 %).   Un réacteur de centrale utilise comme combustible de l'uranium enrichi à 3% en isotope 235. La fission d'un noyau d'uranium 235 se fait avec une perte moyenne de masse de 0,2 u. 30% de l'énergie libérée par fission est transformée en "énergie électrique. La consommation journalière en uranium enrichi d'une centrale est 150 kg. Quelle est la puissance électrique fournie par cette centrale (en MW) ? Energie libérée en J : 931,5*2,3 1024 * 1,6 10-13 = 3,43 1014 J. Puissance thermique (W) =3,43 1014/(24*3600) =3,97 109 W = 3970 MW. Puissance électrique : 3970*0,3 ~1200 MW. Parmi les affirmations suivantes lesquelles sont exactes ? L'émission du rayonnement g ne s'observe que dans la radioactivité a. Faux. Dans une désintégration b+ le nombre de masse de l'atome fils augmente d'une unité. Faux. Le nombre de masse, nombre de nucléons, ne varie pas. Dans une désintégration b- le numéro atomique de l'atome fils augmente d'une unité. Vrai. Dans une désintégration a, il y a émission d'un atome d'hélium. Faux. Emission d'un noyau d'hélium. On peut augmenter l'activité d'un échantillon par chauffage. Faux.     Web www.chimix.com On utilisait autrefois comme unité d'activité le curie (symbol Ci). Un curie correspond à l'activité d'une source contenant 1 g de radium. Données : demi-vie du radium 1590 ans ; masse atomique molaire du radium M = 226 g/mol ; NA= 6,02 1023 mol-1. Déterminer la valeur de 1Ci en GBq. ( 8 ; 16 ; 22 ; 25 ; 37 ; aucune bonne réponse) 1/226 = 4,42 10-3 mol de radium N= 4,42 10-3 * 6,02 1023 = 2,66 1021 noyaux de radium dans 1 g. lt½=ln2 = 0,693 soit l = 0,693 / (1590*365*24*3600)= 1,38 10-11 s-1. activité de 1 g de radium : A= l N= 1,38 10-11 *3,67 1021 = 36,7 1010 Bq= 36,7 GBq. Le polonium 21084Po subit une désintégration de type a. 21084Po = 20682Pb + 42He masse des noyaux en u : 21084Po = 210,0482 ; 20682Pb =206,0385 ; 42He = 4,0015 1 u = 1,66 10-27 Kg ; c= 3 108 m/s. demi vie du polonium 210 : 138 jours Déterminer l'activité ( en Bq) d'un échantillon de polonium 210 dégageant une puissance P= 500 mW. ( 2,4 104 ; 3,5 105 ; 2,7 108 ; 5,1 109 ; 4,1 1010 ; aucune réponse exacte. variation de masse |Dm|=|210,0482-4,0015-206,0385 |= 8,2 10-3 u= 8,2 10-3* 1,66 10-27 =1,36 10-29 kg énergie libérée par chaque désintégration : |Dm| c² = 1,36 10-29 *9 1016=1,22 10-12 J énergie (J) libérée par N noyaux en une seconde 0,5 J /s. d'où N= 0,5 /1,22 10-12 = 4 1011 noyaux lt½=ln2 = 0,693 soit l = 0,693 / (138*24*3600)= 5,81 10-8 s-1. activité A =l N=5,81 10-8 * 4 1011 = 2,32 104 Bq. On considère un noyau de polonium 21084Po. masse d'un neutron : mN= 1,0087 u ; masse du noyau de polonium : m= 210,0482 u ; masse proton mP= 1,0073 u ; 1u = 1,6604 10-27 kg ; 1 eV= 1,610-19 J ; c= 3 108 m/s. Calculer l'énergie de liaison ( MeV/ nuclèons) par nucléons de ce noyau 84 protons et 210-84 =126 neutrons énergie de liaison : El = [84 mP+126mN-m]c² 84 mP+126mN-m=210,048284*1,0073+126*1,0084-210,0482 = 1,661 u 1,661 * 1,6604 10-27 = 2,76 10-27 kg El = 2,76 10-27*(3 108 )²= 2,48 10-10 J 2,48 10-10 /1,6 10-19 = 1,55 109 eV = 1550 MeV 1550 / 210 = 7,4 MeV/nucléons.   La fission d'un noyau d'uranium 235 libère en moyenne une énergie de 200 MeV. Un réacteur nucléaire fournit une puissance de 1300 MW. Le rendement de la transformation d'énergie nucléaire en énergie thermique est de 30 %. Masse d'un atome d'uranium 235 : =m= 235,0435 u. Calculer la consommation annuelle d'uranium 235 (en tonne )du réacteur. 200 106 eV soit 200 106*1,6 10-19 = 3,2 10-11 J. Puissance thermique : 1300 106/0,3 = 4,3 109 W énergie thermique produite en une année : 4,3 109*365*24*3600 = 1,37 1017 J. nombre de fission en une année : 1,37 1017 / 3,2 10-11 = 4,27 1027 fissions. soit 4,27 1027 atomes d'uranium 235 ayant été consommés. masse d'un atome d'uranium 235 : 235,0438*1,66 10-27 = 3,9 10-25 kg. perte de masse : 4,27 1027* 3,9 10-25 kg = 1,66 103 kg vosin 1,7 tonnes. Le plutonium 23894Pu est un émetteur a très puissant. Chaque désintégration libère une énergie de 5,48 MeV. On considère une source de masse m= 150 mg de plutonium 238. Cette source dégage une puissance P= 85 mW 1 eV= 1,6 10-19 J ; masse atomique du plutonium 238 : 238,1 u ; 1 u = 1,661 10-27 kg. Calculer la demi-vie ( en années ) du plutonium 238. ( 86 ; 128 ; 245 ; 412 ; 510 ; aucune bonne réponse) m = 1,5 10-4 kg et masse atomique du plutonium = 238,1*1,6110-27= 3,954 10-25 kg nombre initiaux de noyaux de plutonium : N0= 1,5 10-4 / 3,954 10-25 =3,79 1020. activité initiale A0 = 0,085 / (5,48 *1,6 10-19)==9,69 1010 Bq l= A0 = / N0 = 9,69 1010 /3,79 1020= 2,56 10-10 s-1. t½ = ln2 / l= 0,693 /2,56 10-10 = 2,7 109 s = 86 ans.   On analyse tous les ans une source radioactive de césium 137. On détermine à l'instant t de l'analyse l'activité A(t) de la source. On constate que A(t) / A(t+1) = 1,023 avec t en années. Calculer le temps de demi-vie du césium 137. (10 ; 20 ; 30 ; 40 ; 50 ; aucune réponse exacte) A(t) =A0 exp(-lt) ; A(t+1) =A0 exp(-l(t+1)) A(t) / A(t+1) = exp(-lt) exp(l(t+1)) = exp(l) ; l = ln(A(t) / A(t+1) = ln 1,023 = 2,27 10-2 an-1. Or l t½=ln2 d'où t½=ln2 / l =ln2 / 2,27 10-2 = 30 ans. Texte : une source contient une masse m = 1,50 g de bismuth 21283Bi, nucléide radioactif de type a. On mesure le volume d'hélium produit par cette source en 1 min et on trouve V= 1,93 mL. Vm = 24,0 L/mol ; NA = 6,02 1023 mol-1 ; 1 u = 1,66054 10-27 kg ; masse d'un atome de bismuth 212 : 211,95 u. Analyse : Question relative à la demi-vie ( min) du bismuth 212. (30 ; 40 ; 50 ; 60 ; 70 ; aucune réponse exacte) Exprimer les quantités de matière en mol : nHe = V/Vm = 1,93 10-3 / 24 = 8,04 10-5 mol. Masse molaire du bismuth : M = 211,95 * 1,66054 10-27 * 6,02 1023 =0,21187 kg/mol = 211,9 g/mol n(Bi initiale) = m/M = 1,50 / 211,9 = 7,08 10-3 mol. n(Bi finale) =7,08 10-3 -8,04 10-5 =6,998 10-3 mol. Loi de décroissance radioactive : N(t) = N0 exp(-lt) ; ln(N0/N)= lt ; l = ln(N0/N) / t Soit avec t = 1 min et les valeurs numériques précédentes : l =ln(7,08 / 6,998) ; l = 1,165 10-2 min-1. Or l t½ = ln 2 d'où t½ = ln2/ l = 0,693 / 1,165 10-2 ; t½ = 60 min.

retour -menu