Concours kiné berck : 9 années de QCM condensateur, dipôle RLC. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

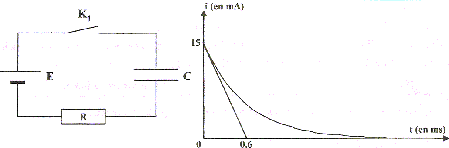
Décharge d'un condensateur à travers un conducteur ohmique R=33 000 ohms. La constante de temps vaut t= 11,4 s. Tension initiale aux bornes du condensateur : U=12 V Quelle est l'énergie maximale (mJ) emmagasinée dans le condensateur ? Constante de temps t = RC=11,4 d'où C=11,4/33 000 = 0,345 10-3 F. énergie maxi : ½CU² = 0,5*0,345 10-3*122 =0,0249 J = 24,9 mJ. Un circuit RLC comporte un condensateur (C=10 mF) et une bobine d'inductance 180 mH. Initialement le condensateur est chargé sous une tension de 15 V. Au bout de 100 oscillations, l'énergie électrique initialement emmagasinée dans le condensateur a diminué de 80%. Calculer la puissance moyenne (en mW) dissipée dans ces 100 oscillations. Période du dipole LC : T= 2p(LC)½ = 6,28 *(0,18*10-5)½ = 8,43 10-3 s. 100 périodes = 0,843 s Energie initiale stockée dans le condensateur : ½CU² = 0,5 *10-5*152 =1,12 10-3 J énergie perdue : 0,8 *1,12 10-3 =9,0 10-4 J puissance (W) = énergie perdue (J) / durée (s). P= 9,0 10-4 /0,843 =1,1 10-3 W = 1,1 mW. Répondre par vrai ou faux. La décharge d'un condensateur à travers une résistance est d'autant plus rapide que la constante de temps est grande. Faux. t=RC ; la durée de la décharge est voisine de 5t. La durée de la décharge est proportionnelle à R. Pour augmenter la constante de temps d'un circuit RC on peut diminuer la capacité du condensateur. Faux. La constante de temps t est le temps au bout duquel la charge et la décharge d'un condensateur sont réalisées à 63%. Vrai. Lorsqu'on écarte les armatures d'un condensateur plan électriquement isolé, l'énergie emmagasinée par le condensateur diminue. Faux. L'énergie augmente du travail fourni par l'opérateur pour écarter les armatures. Dans un circuit RC l'intensité du courant s'annule lorsque la charge du condensateur est terminée. Vrai.   Un générateur délivrant une tension constante E=4 V alimente l'association en série d'un condensateur de capacité C= 100 nF initialement déchargé et d'un conducteur ohmique de résistance R = 4700 ohms. On prend comme origine des temps l'instant où débute la charge. La tension aux bornes du condensateur varie au cours du temps suivant la relation uc(t) = E(1- exp (-t/(RC))). Au bout d'un temps t = 5,2 10-4 s quel pourcentage de sa valeur finale vaut la tension aux bornes du condensateur ? RC = 4,7 103 * 100 10-9 = 4,7 10-4 s puis calculer : t / (RC) = 5,2 / 4,7=1,1 puis calculer u/E = 1 - exp (-1,1)=0,67 ( 67 %) K1 est fermé et K2 est ouvert : On charge le condensateur de capacité C= 10 microfarads par le générateur de force électromotrice E= 7 V et de résistance interne négligeable. K1 est ouvert et K2 est fermé : Le condensateur chargé est relié à une bobine d'inductance L= 50 mH et de résistance négligeable. On prendra comme origine des temps la fermeture de K2. Au bout de combien de temps ( en ms) la tension aux bornes du condensateur sera t-elle minimale pour la première fois ? période T= 2p (LC)½=2*3,14(0,05*10-5)½ = 4,44 ms. à t = 0,25 T = 1,11 ms le condensateur est déchargé pour la première fois. à t = ½T= 2,22 ms le condensateur est chargé en sens contraire de la charge précédente ; la tension à ces bornes vaut - 7V. On considère le circuit ci-dessous L'interrupteur K est placé en position1 jusqu'à obtention du régime permanent. On bascule ensuite K en position 2. Cet instant est considéré comme instant initial. R= 33 ohms ; E= 12 V ; L= 58 mH ; r= 27 ohms. Déterminer la valeur de l'énergie stockée dans la bobine en mJ au bout de 1,4 ms. t = L/ (R+r) =0,058 / (33+27) = 0,967 ms. I0 = E/r = 12/27 = 0,444 A i(t) = I0 e-t/t = 0,444 e -1,4 / 0,967 = 0,104 A énergie stockée dans la bobine : E = ½Li² E = 0,5*0,058 * 0,104² = 3,16 10-4 J = 0,316 mJ = 316 mJ. Une bobine d'inductance L et de résistance r=5,4 ohms est parcourue par un courant dont l'intensité varie commel'indique la figure.  Déterminer la valeur de L ( mH) pour que la tension aux bornes de la bobine soit nulle à la date t=50 ms. coefficient directeur de la droite di/dt = - 3/0,1 = -30 A/s ; i(t= 50 ms) = 1,5 A ( lecture graphe) tension aux bornes de la bobine : u = L di/dt + ri =0 L(-30) + 5,4*1,5 = 0 d'où L= 0,27 H = 270 mH.     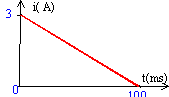Web www.chimix.com Un condensateur initialement déchargé de capacité C et un conducteur ohmique R sont associés en série aux bornes d'un générateur idéale de tension de force électromotrice E= 9,0 V. A l'instant t=0, on ferme l'interrupteur K et on relève l'intensité du courant dans le circuit en fonction du temps t. Déterminer les valeurs de la résistance R (kW) et de la capacité C (mF). à t= 0 le condensateur est déchargé ( la tension à ces bornes est nulle) et la tension aux bornes du résistor est E=9V, alors que l'intensité du courant vaut 0,015 A. d'où R = E/I= 9 /0,015 = 600 W soit 0,6 kW. La constante de temps du circuit vaut t= 0,6 ms ( mlecture graphe) soit RC= 6 10-4 s. C= t / R = 6 10-4 / 600 = 10-6 F = 1 m F. Une petite bille de forme parfaitement sphérique de rayon 5 mm et de masse volumique r= 2,0 103 kg/m3, tombe au centre d'un tuyau cylindrique de rayon 50 cm remplie d'eau. La bille est initialement à 1 m au dessus de la surface de l'eau. On néglige les frottements de l'air. L'origine des temps est prise à l'instant du contact avec l'eau. Le niveau de référence pour l'énergie potentielle est la surface de l'eau. On prendra g = 10 N/kg ; p~3 ; 20½~4,5. L'énergie potentielle de pesanteur initiale de la bille est 1 J. Faux. Volume de la bille V=4/3pr3~4*(5 10-3)3=5 10-7 m3. Masse de la bille : m = rV=2 103*5 10-7 =10-3 kg. Energie potentielle initiale Ep =mgh = 10-3*10*1 = 0,01 J. La vitesse de la bille à l'instant où elle touche l'eau est de l’ordre de 10 m/s. Faux. La bille est en chute libre : on choisit un axe vertical orienté vers le bas dont l'origine est la position initiale de la bille. z=½gt2 ; z=5t2 ; v=gt = 10 t soit v2 = 2gh = 20 : v~4,5 m/s. L'énergie cinétique perdue par la bille au cours du choc est transférée au milieu liquide. On observe des ondes progressives transversales à la surface de l'eau se propageant dans toutes les directions à partir du point d'impact. L'onde touche le bord de la cuvette à l'instant t=0,1 seconde. La célérité des ondes à la surface de l'eau est de 5 m.s-1. Vrai. 0,5 m parcouru en 0,1 s : c= 0,5/0,1 = 5 m/s. La célérité de l'onde est modifiée si la goutte tombait de 50 cm de haut au lieu de 1 m. Faux. L'énergie transmise au milieu liquide serait plus petite. La vitesse dépend des caractéristiques du milieu de propagation de l'onde. On considère un solide ponctuel de masse m=1 kg glissant, sans vitesse initiale, à partir du point A sur un demi-cercle vertical de rayon de 1 m et prolongé par une piste horizontale BC, de 2 m de longueur, caractérisée par une force de frottements F= m R avec m =0,25 et R réaction normale entre le support et le solide. Le solide M continue son trajet et percute alors un ressort de raideur k qu'il comprime de 10 cm. On donne g=10 m s-2 ; 10½~3,15. La vitesse que doit avoir la masse au point B est vB=6 m/s. Faux. Ecrire le théorème de l'énergie cinétique entre A et B : DEc = ½mv2B-0. Travail moteur du poids en descente : mgr = 10 J. Entre A et B, il n'y a pas de frottement ; l'action du plan est perpendiculaire à la vitesse : son travail est donc nul. par suite : ½mv2B=mgr= 10 ; v2B=20 ; v~ 4,5 m/s. Le travail effectué par la force de frottements entre B et C est WBC=5 J. Faux. La force de frottement est colinéaire à la vitesse mais de sens contraire ; WBC = -F BC = - m R BC avec de plus R=mg = 10 N WBC = -0,25*10*2 = - 5 J. La vitesse du solide au point C est vC=3,15 m/s. Ecrire le théorème de l'énergie cinétique entre A et C : DEc = ½mv2C-0. Travail moteur du poids en descente : mgr = 10 J. Le poids, perpendiculaire à la vitesse, ne travaille pas entre B et C. Travail résistant des frottement : -5 J ; somme des travaux : 5 J. ½mv2C=5 ; v2C=10 ; vC=3,15 m/s. Vrai. La constante de raideur de ce ressort est de 1000 N.m-1. Vrai. Au cours de la compression du ressort, l'énergie cinétique en C est convertie en énergie potentielle élastique : ½mv2C=5 = ½kDx2 ; k =10/ Dx2 =10/0,12 = 1000 N m-1.

retour -menu