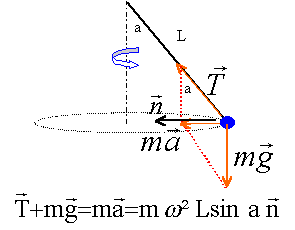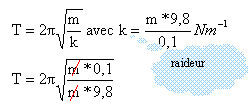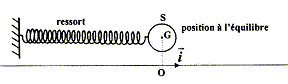Concours kiné berck : 9 années de QCM pendule, ressort. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Une bille de masse m=90 g est suspendue en un point A par un fil inextensible de longueur L=80 cm et de masse négligeable. Le pendule ainsi constitué est mis en mouvement de rotation uniforme autour de l'axe vertical passant par le point A avec une vitesse angulaire de 10 rad/s. g=9,8 m/s² Calculer la tension du fil (en N). T sin a = m w² L sin a ; T =m w² L ; masse en kg et longueur en m T= 0,09*100*0,8 =7,2 N. Un ressort attaché à un point fixe soutient une masse m sous le poids de laquelle il s'allonge de 10 cm. Quelle est la période des oscillations harmoniques du système en s ? A l'équilibre le poids est opposé à la tension : ces deux forces ont même valeur : mg = kDx T= 2*3,14 [1/98]½ =0,63 s.   Un pendule simple est constitué d'un fil de longueur L, accroché à un point fixe O et auquel est suspendu un solide ponctuel de masse m. On écarte le pendule de sa position initiale d'un angle q et on le lâche avec une vitesse initiale v0 perpendiculaire à la trajectoire. On prendra comme origine de l'énergie potentielle de pesanteur la position d'équilibre du solide. Données : q = 12° ; L= 0,62 m ; v0 =0,75 m/s ; m = 100g. Déterminer l'énergie potentielle maximale (en mJ) du système. Energie mécanique initiale : ½ mv02 + m g L( 1 - cosq) L'énergie mécanique finale au point le plus haut est sous forme potentielle. Conservation de l'énergie mécanique : Ep max = m[0,5v02 + g L( 1 - cosq)]. Ep max =0,1[0,5*0,752 +9,8*0,62(1-cos12)]=0,1( 0,281+0,133)= 0,041 J = 41 mJ. Un solide S de masse m glissant sans frottement sur une tige horizontale, est accroché à un ressort idéal de raideur k dont l'autre extrémité est fixée à un support. La position du centre d'inertie G du solide à l'équilibre constitue l'origine O de l'axe des abscisses. On écarte le solide de sa position d'équilibre, de 5 cm dans le sens des abscisses et on le libère sans vitesse initiale. L'origine des temps sera prise au premier passage du centre d'inertie à la position d'équilibre. L'énergie du système {solide + ressort} est constante et égale à 20 mJ. A la date t= 50 ms, l'énergie potentielle élastique du système est de 4,9 mJ. Déterminer la masse ( en g) du solide. Energie mécanique EM= énergie cinétique Ec + énergie potentielle élastique Ep. EM= ½mv² + ½kx² Si x= 0,05 m ( l'amplitude) Em est sous forme d'énergie potentielle élastique : 0,02 = ½ka² k = 2*0,02 / (0,05)² = 16 N/m. A t = 0,05s : ½kx² = 4,9 10-3 J d'où x² = 9,8 10-3 /16= 6,125 10-4 m² ; x= 2,475 10-2 m. x(t) = A sin (w0t) à t = 0 x(t=0) doit être nul. x(t=0,05 ) = 2,475 10-2 = 0,05 sin(w0*0,05) sin(w0*0,05) = 0,495 = sin 0,518 (rad) soit w0*0,05 =0,518 w0= 0,518/0,05 = 10,356 rad/s. Or w²0= k /m d'où m = k / w²0= 16/ 10,356² = 0,150 kg = 150 g.     Web www.chimix.com Un oscillateur est constitué par un solide S ponctuel de masse M accroché à l'extrémité d'un ressort à spires non jointives, de masse négligeable et de constante de raideur k. S oscille sans frottement sur une table horizontale. On repère la position à l'instant t de S sur un axe horizontal dont l'origine correspond à la position de S au repos. On écarte S de 3 cm de sa position d 'équilibre dans le sens des abscisses positives et on le lâche sans vitesse initiale. L'origine des temps est prise au premier passage du solide S par la position d'équilibre. L'équation horaire est de la forme x(t) = Xm cos (2p/T0t+j). Données : M=150g ; k=20 N/m Déterminer l'énergie cinétique (en mJ) à la date t=0,3 s.(8,1 ; 12,3 ; 16,4 ; 21,6 ; 31,4 ; aucune réponse exacte) période T0= 2*3,14 racine carrée (0,150/20)=0,544 s et 2p/T0 = 11,54 rad/s vitesse, dérivée de x par rapport au temps v(t)=Xm (-2p/T0)sin (2p/T0t+j). à t=0 la vitesse est maximale et l'abscisse est nulle x(0) =0= Xm cos (j) d'où j= ½p ou 3p/2. v(0)=Xm (-2p/T0)sin (j) avec Xm = 0,03 m le solide se déplace en sens contraire de l'axe donc j = p/2 v(0,3 )=0,03 (-11,54)sin (11,54*0,3+p/2). v(0,3 ) = -0,346 *(-0,95) = 0,328 m/s énergie cinétique :½mv²=0,5*0,15*0,328²= 8,1 10-3 J= 8,1 mJ.   Un oscillateur est constitué par un solide de masse m attaché à l'extrémité d'un ressort à spires non jointive, de masse négligeable et de constante de raideur k=8 N/m. Le solide S oscille sans frottement selon l'axe horizontale Ox. On repère la position, à l'instant t, du centre d'inertie G de S par l'abscisse x(t). L'origine O du repère correspond à la position du centre d'inertie G à l'équilibre. L'équation horaire du mouvement s'écrit : x(t) = 8,00 10-2 cos(10,8 t + 0,723) avec les unités S.I. Parmi les affirmations suivantes combien il y en a-t-il d'exactes ? - A l'instant t=0, le solide est lâché sans vitesse initiale. faux. x'(t) = -0,08*10,8 sin(10,8 t + 0,723) ; x'(0) = -0,08*10,8 sin(0,723)=-5,72 10-2 m/s. - L'énergie mécanique de l'oscillateur est 7,2 mJ.faux. Lorsque x=xm=0,08 m, l'énergie mécanique est sous forme potentielle élastique ½kxm2 =0,5*8*0,082 =2,56 10-2 J. - La vitesse maximale du solide est 0,86 m/s.exact. x'(t) = -0,08*10,8 sin(10,8 t + 0,723) ; x'm =0,08*10,8 =0,86 m/s. - La masse du solide est 52 g. faux. w0 = 10,8 rad/s ; w02=k/m ; m = k/w02=8/10,82 =6,86 10-2 kg = 68,6 g. - L'accélération maximale du solide est 9,3 m/s². exact. x"(t) = -0,08*10,82 cos(10,8 t + 0,723) ; x"m(t) = 0,08*10,82 = 9,3 m/s².

retour -menu