Concours kiné berck : 9 années de QCM électricité, moteur, photopile, puissance, rendement. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Un moteur électrique de fcem E'=2,4 V et de résistance interne r' est monté en série avec un conducteur ohmique de résistance R=6 ohms , une pile (E=4,5V r=1,9ohms), un ampèremètre de résistance négligeable et un interrupteur K. Le moteur se met à tourner et l'ampèremètre indique 0,2 A. Déterminer la valeur de la résistance interne du moteur.(en ohm). Additivité des tensions : 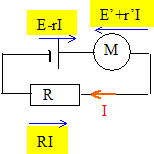E-rI = E'+r'I+RI d'où r' =(E-E')/I -R-r = (4,5-2,4)/0,2-6-1,9 =2,6 W. Le moteur d'une grue soulève une charge de 30 000 N à la vitesse de 15 m/min. La tension d'alimentation continue du moteur est U=230V et l'intensité du courant vaut I=45 A. Le rapport de la puissance mécanique fournie à la puissance électrique utile du moteur (rendement mécanique) est de 75%. Quelle est la résistance r du moteur (en ohm) ? 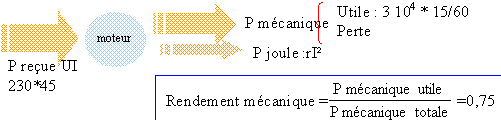Puissance mécanique utile à la montée de la charge (W) = force (N)*vitesse (m/s). 15 m/min = 15/60 m/s = 0,25 m/s. Pméca =3 104*0,25 =7,5 103 W Puissance mécanique totale : Pméca /0,75 = 104 W Puissance électrique reçue par le moteur : Preçue =UI = 230*45 =1,035 104 W Preçue =Pméca totale +Pjoule ; Pjoule = (1,035-1)104 = 350 W Pjoule = rI2 soit r = Pjoule /I2 =350/452 =0,17 W.   Données : tension aux bornes d'un moteur U=E' + r'i ; E=6 V ; r = 8 ohms ; R1= 10 W ; R2 = 15 W ; R3 = 17 W ; E'=2 V ; r' = 5 W. 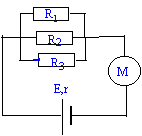Calculer la valeur de l'intensité i (mA) du courant délivré par le générateur. Les résistors sont en dérivation : les conductances (inverse d'une résistance )s'ajoutent. G total = 1/ 10 + 1/15 + 1/17 = 0,2255 S soit R équivalent = 1/0,2255 = 4,43W. intensité I = (E-E') / (Réquivalent + r) = 4/ 17,43 = 229 mA. On considère un générateur de fem E et de résistance interne r. Il fournit un courant d'intensité i et la tension à ces bornes est de 5,4 V. En une heure de fonctionnement ce générateur fournit au circuit une énergie de 9,4 kJ. Le rendement électrique de ce générateur est h=0,85. Déterminer la valeur de la fem E ( V) de ce générateur. Rendement h = U/E d'où E = U/h = 5,4 / 0,85 = 6,4 V.  On considère une photopile de surface 120 cm² exposée dans un lieu qui reçoit en moyenne une énergie solaire au niveau du sol de 1400 kWh m-2 par an. Dans ces conditions la photopile fournit une puissance électrique de 600 mW. Donnée : 1 Wh = 3600 J. Calculer le rendement (en %) de cette photopile. (27,4 ; 31,3 ; 34,2 ; 37,8 ; 39,5 ; aucune réponse exacte) 120 cm² = 0,012 m² puissance solaire par m² : 1400 *1000 *3600 / ( 365*24*3600)=1,4 106 / (365*24)=159,8 W m-2. puissance photopile par m² : 0,6 / 0,012 = 50 W m-2. rendement 100* 50/159,8 = 31,3 %.     Web www.chimix.com On considère une pile de fem E, de résistance interne r, délivrant un courant d'intensité I. Combien y a-t-il d'affirmations exactes ? - La tension aux bornes de la pile peut être supérieure à sa fem E ( faux) " U= E-rI " - La pile s'échauffe quand elle fonctionne (vrai ) - La pile dissipe par effet joule pendant la durée Dt une énergie égale à : rI²Dt (vrai ) - La tension aux bornes de la pile est proportionnelle à l'intensité du courant qu'elle délivre ( faux) " E-U est proprotionnel à I" - L'énergie électrique totale délivrée par la pile pendant la durée Dt se calcule par la relation EI²Dt ( faux) " E I Dt " On considère une pile de fem E= 12 V et de résistance interne r= 0,8 W. La puissance utile fournie par cette pile au reste du circuit est Pu=5,4 W. Calculer l'intensité du courant ( en A) débité par cette pile.(0,12 ; 0,24 ; 0,37 ; 0,46 ; aucune réponse exacte ) tension aux bornes de la pile : U= E-rI=12-0,8 I puissance utile P=UI = (12-0,8 I )*I ; 5,4 = 12 I -0,8 I² ; résoudre l'équation du second degré : d'où I= 0,46 A. Un condensateur de capacité C est initialement déchargé. On l'associe en série avec un résistor R. Cet ensemble est alimenté par un générateur idéal de tension continue de fem E= 14,0 V. A t=0 on ferme l'interrupteur et on relève les variations de la charge q de l'armature positive du condensateur en fonction du temps. 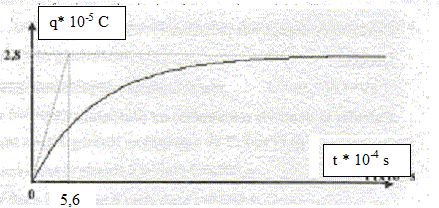Déterminer la valeur de R (ohms) (280 ; 420 ; 680 ; 920 ; 1200 ; aucune réponse exacte) [dq/dt]t=0 =I0 = 2,8 10-5 / 5,6 10-4 = 0,05 A E = RI0 d'où R= 14/0,05 =280 W.   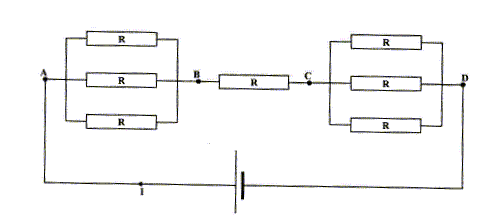UAD=7,5 V Calculer UBC (V). ( 1,0 ; 2,5 ; 3,5 ; 4,5 ; 7,5; aucune réponse exacte ) UBC =RI ; UAB=UCD=R/3 I=UBC /3. additivité des tensions : UAD=UAB+UBC +UCD=UBC /3 + UBC + UBC /3 =5UBC /3 UBC =3UAD/5 =3*7,5/5 =4,5 V.

retour -menu