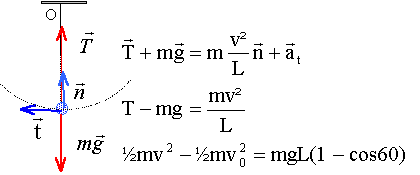Pendule simple.  En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

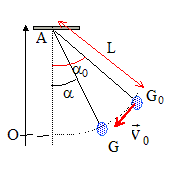
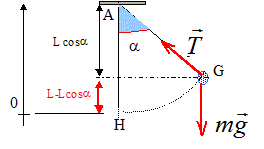
pendule simple. Texte : m= 50 g ; L = 0,50 m ; a0 = 60° ; vitesse initiale v0 = 2,0 m/s. On néglige les frottements. Analyse : Question relative à la vitesse v. Ecrire le théorème de l'énergie cinétique entre G0 et G : La tension, perpendiculaire à la vitesse ne travaille pas. Travail moteur du poids : mg L(cosa- cosa0) Variation d'énergie cinétique : ½mv2 -½mv02. ½mv2 -½mv02 =mg L(cosa- cosa0) v2 = v02+2g L(cosa- cosa0).  Question relative à la tension T. . Question relative au passage à la position d'équilibre a=0. vitesse : v2 = v02+2g L(1- cosa0). v2 = 4 + 2*10*0,5(1-0,5) =9 ; v = 3 m/s. tension : T = m(g +v2/L). T = 0,05*(10 + 9/0,5) =1,4 N.   Période du pendule et gravité. Texte : un pendule simple bat la seconde ( T= 2 s) au niveau de la mer. On l'amène à une altitude h = 5000 m. Analyse : Question relative à la variation de la période. T0 = 2p(L/g)½. à l'altitude h =5000 m, g est plus petit qu'au niveau de la mer : pour conserver la même période il faut diminuer L, la longueur du balancier.     Web www.chimix.com Jambe d'un marcheur. Texte : on assimile la jambe d'un marcheur à un pendule simple de longueur L. La marche s'efectue à vitesse constante v ; le pas est régulier de longueur d. Analyse : Question relative à relation entre la vitesse v et la longueur L. période du pendule simple : T= 2p[L/g]½ ; pulsation ( rad/s) w = 2p / T =[g/L]½ ; q(t) = q0 sin ( w t) ; q'(t) = w q0 cos( w t) = [g/L]½q0 cos ( w t) vitesse linéaire v = q'(t) L =[g/L]½ Lq0 cos ( w t) = [gL]½ q0 cos ( w t). 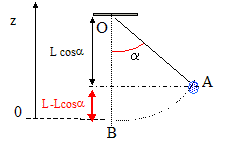pendule : aspect énergétique. Texte : masse m= 10 g ; longueur L= 1 m ; a0 = 8° ; vitesse initiale nulle. Les frottements sont négligés. Analyse : Question relative à l'énergie mécanique.   Energie mécanique initiale = énergie potentielle de pesanteur = mg L (1-cos a0) = 0,01*10*1(1-0,99) = 0,1*0,01 = 10-3 J = 1 mJ. Question relative à la vitesse maximale. Energie mécanique au passage à la position d'équilibre = énergie cinétique = ½mv2max. Conservation de l'énergie mécanique : Em =½mv2max. ; v2max. = 2Em /m. vmax = [ 2/10]½ = 0,45 m/s. Question relative à la vitesse si" l'énergie cinétique vaut le quart de l'énergie mécanique". ½mv2 = 0,25 Em =0,125 m v2max ; v2 =0,25   v2max ; v = 0,5 vmax.

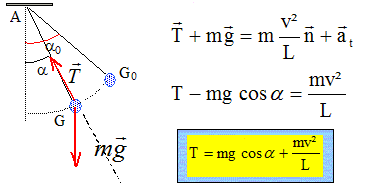retour -menu