Analyse détaillée d'exercices réalisés sous forme de QCM. Accélération. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

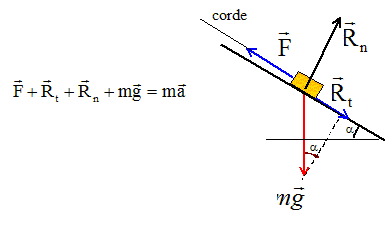
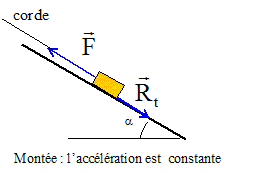
Montée du plan incliné. Texte : Masse du solide m = 40 kg ; RT = 100 N. Analyse : Question relative aux forces. Le solide est soumis à son poids, à l'action du plan et à la tension de la corde. Question relative à Rn perpendiculaire au plan. Ecrire la seconde loi de Newton suivant un axe perpendiculaire au plan : -mg cos a + Rn = 0 ; Rn = mg cos a. A.N : m =40 kg ; a = 30° ; Rn = 40*10*cos 30 = 346 N.  Question relative à F ou à l'acélération a. Ecrire la seconde loi de Newton suivant un axe parallèle au plan : F - mg sin a -Rt = ma. a = (F-Rt ) / m -g sin a. F = Rt + m(a+g sin a). A.N : si a = 1 ms-2 alors F = 100 +40(1+10 sin 30) = 340 N. si F = 500 N alors a =(500-100)/40 -10 sin 30 = 10-5 = 5 m s-2.   Chute verticale sans vitesse initiale. Texte : Analyse : Question relative aux forces. A l'instant initial, la vitesse étant nulle, la bille est immobile et les forces de frottements fluide sont nulles. Initialement la bille est soumise à son poids et à la poussée d'Archimède. Question relative à l'accélération initiale. Ecrire la seconde loi de Newton sur un axe vertical orienté vers le bas : mg- V reaug = ma ; V r g- V reaug = V r a ; r g- reaug = r a ; a =(1 -reau/r) g. a = (1-1/2,7) *10 = 6,3 m s-2.     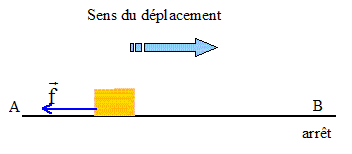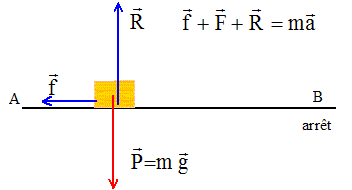Web www.chimix.com Freinage d'un véhicule. Texte : Masse m = 400 kg ; vitesse initiale en A : v0 = 5 m/s ; force de freinage f constante. La distance AB est parcourue en 14,3 s. Analyse : Question relative aux travaux des forces. Le poids et l'action normale du plan sont perpendiculaires la vitesse : ces forces ne travaillent pas entre A et B. Travail résistant de la force de freinage entre A et B : W=-f AB Question relative à l'accélération. accélération : a = Dv/Dt = (0-v0 ) / Dt =-5/14,3 = -0,35 m/s². Question relative à la valeur de force f. Ecrire la seconde loi de Newton sur un axe horizontal orienté dans le sens du mouvement : -f = ma ; f =400*0,35 = 1,4 102 N. Question relative à la distance AB d'arrêt. Ecrire le théorème de l'énergie cinétique entre A et B : 0-½mv02 = -f AB = m a AB AB = v02 /(-2a) ; AB = 52/ 0,70 = 36 m.   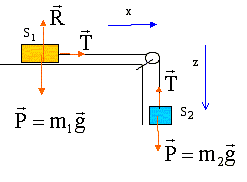Texte : la poulie a une influence négligeable sur le mouvement. Le fil est inextensible et de masse négligeable. Les frottements sont négligés. Analyse : Question relative à l'accélération.   La masse de la poulie étant négligeable, les deux solides ont la même accélération et les tensions sont identiques. écrire la seconde loi de Newton : pour S1 suivant l'axe x : T=m1a pour S2 suivant l'axe z : -T+m2g=m2a ; T = m2(g-a) m1a =m2(g-a) d'où a = m2g / (m1+m2).

retour -menu