|
|
| .
. |
|
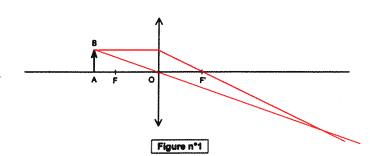
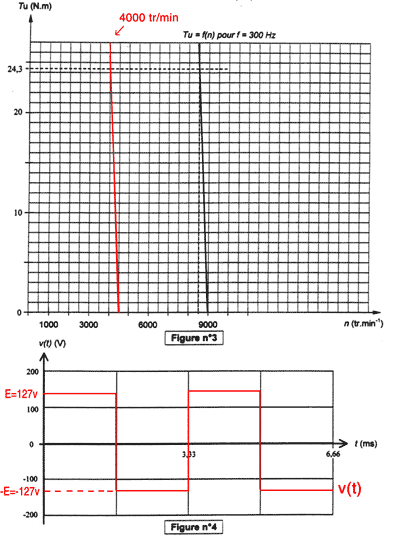
optique : La figure n°1 du document-réponse représente une lentille devant laquelle est placé un objet AB.
corrigé Le sens des flèches permet de dire que c'est une lentille convergente.2) C'est la distance focale. d = 10 dioptries OF' = 1/ 10 = 0,1 m
- Les rayons passants par le centre optique (point O) ne sont pas déviés. - Les rayons parallèles à l'axe optique ressortent en passant par le foyer l'image F'.
|
|
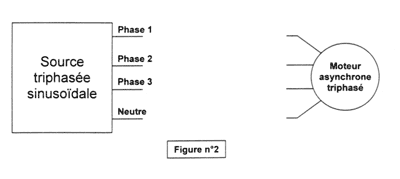
moteur asynchrone : Un constructeur automobile propose une voiture électrique à moteur asynchrone triphasé dont la source électrique est réalisée à l'aide d'un onduleur, lui-même alimenté par un ensemble de batteries. 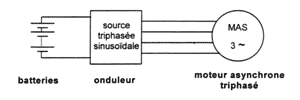
Les partie A et B de ce problème peuvent être traitées indépendamment l'une de l'autre. A - Etude du moteur (13 points) Le moteur asynchrone triphasé, dont les enroulements du stator sont couplés en étoile, est alimenté par une source triphasée équilibrée sinusoïdale de tension efficace et de fréquence réglables.
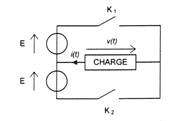
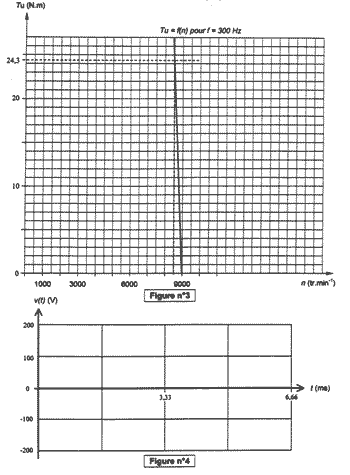
B - Etude de l'onduleur (4 points) Le schéma suivant représente le modèle simplifié d'une partie de l'onduleur: E = 127 V. K1 et K2 sont des interrupteurs parfaits. Entre 0 et T/2 : K1 fermé et K2 ouvert. Entre T/2 et T : K1 ouvert et K2 fermé. La charge est inductive. T désigne la période de fonctionnement des interrupteurs.
corrigé C'est l'inducteur : il engendre un champ magnétique tournant. Car le rotor tourne à une vitesse légèrement plus faible que celle du champ tournant (appelée vitesse de synchronisme).
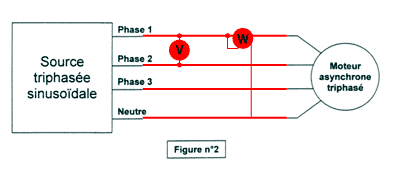
La plaque du moteur indique 127 V / 220 V. Chaque phase du moteur doit donc supporter 127 V (la plus faible des deux tensions). A partir du réseau 127 V/ 220 V, il faut donc coupler le moteur en étoile pour que chaque enroulement se retrouve sous la tension simple 127 V. Au point nominal : PA = 3 V I cosj =3 * 127 * 80 * 0,79 = 24 kW rendement h =Pu /Pa soit Pu = Pa * h = 24*0,9 = 21,6 kW.A En étoile, chaque enroulement est parcouru par le courant de ligne IN d'où PJS = 3 rI²N pour les trois enroulements. PJS = 3 * 0,1 * 802= 1,92 kW
Wattmètre : P = PA / 3 = 8 kW Voltmètre : U = 220 V n voisin de ns = f/p *60 d'où p = 60 f / n = 300*60 / 8500 = 2,1 p = 2 (entier le plus proche) Pu=TuW avec W = 2pn/60 d'où Tu = 60 Pu/(2pn) = 60*21600/(6,28*8500) = 24,3Nm. U/ f = U' / f ' = constante d'où U' = Uf ' / f = 150*220/300 = 110 V.
Pour le tracé, c'est la droite qui passe par les points : T'U = 24,2 N.m ; n = 4000 tr/min Et T'U = 0 N.m ; n's = ns/2 = 4500 tr/min Les deux courbes sont parallèles. Etude de l'onduleur Conversion tension continue courant alternatif. v(t) = E quand K1 fermé. v(t) = - E quand K2 fermé. v(t) est carrée alternative de valeur | v(t) | = E = 127 V donc V = E = 127 V
retour - menu |