Le primaire du transformateur étudié est alimenté par le réseau EDF sous une tension de valeur efficace V_1N = 225 V et de fréquence f = 50Hz.

1. Essai n°1 : on a réalisé un essai en continu; le schéma du montage est représenté sur la figure 3, ci-dessous. S_c désigne une source de tension continue réglable. On a mesuré : V_1c = 12V; I_1c = 3,64 A.
   - Calculer la valeur de la résistance R₁ du primaire.
2. Essai n°2 : il s'agit d'un essai à vide réalisé sous tension primaire minimale V₁₀= V_1N . On a mesuré les grandeurs suivantes : I₁₀ = 0,24 A : valeur efficace de l'intensité du courant absorbé par le primaire. V₂₀ = 48,2 V: valeur efficace de la tension secondaire à vide. P₁₀= 10,2 W : puissance absorbée par le primaire.
   - Calculer le rapport de transformation ou rapport du nombre de spires .
   - Evaluer les pertes par effet Joule dans ce fonctionnement.
   - En déduire la valeur des pertes dans le fer à vide et justifier l'emploi de cette même valeur en charge sous tension primaire minimale.
3. Essai n°3 : le secondaire est court-circuité et le primaire alimenté sous tension réduite. Le courant secondaire de court-circuit I_2cc est égal au courant secondaire nominal, I_2n pour Le courant absorbé par le primaire est alors I_cc=0,86 A.
   - Sachant que, dans cet essai, le transformateur peut être considéré comme parfait pour les courants, calculer la valeur du courant secondaire de court-circuit, I_2cc.
   - Calculer la valeur de l'impédance totale ramenée au secondaire, Z_s.
4. Essai en charge nominale : le schéma du montage est représenté sur la figure 4 ci-dessous ; le transformateur est alimenté sous tension primaire nominale. Pour simuler la charge, on utilise une bobine sans noyau de fer, équivalente à un circuit RL série. Son impédance est Z= 11,6 W et son facteur de puissance cos j = 0,89. Le wattmètre mesure P₁= 180 W et la pince ampèremétrique I ₂= 4 A.
   - Calculer la tension secondaire en charge, V₂
   - Montrer que la résistance R de la bobine est 10,3 W. En déduire la puissance active P₂ consommée par cette charge.
   - Déterminer le rendement du transformateur au cours de cet essai.
   - En déduire la valeur des pertes par effet Joule du transformateur.
   - Le modèle équivalent du transformateur, ramené au secondaire, est donné sur le document-réponse 2 ci-dessous ; compléter ce document en précisant la valeur de R_s et de X_s. Les calculs seront justifiés.

 

 

---

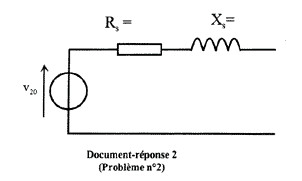
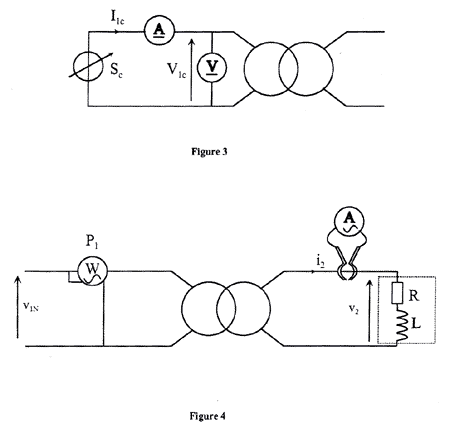
corrigé

---

Essai n°1

en continu : R₁ = V_1c / I_1c = 12 / 3,64 = 3,3 W.

Essai n°2 :

rapport de transformation m = V₂₀ / V₁₀ = 48,2 / 225 = 0,214.

pertes par effet Joule dans ce fonctionnement : P_J0 = R₁I²₁₀ = 3,3*0,24² = 0,19 W.

pertes dans le fer à vide = puissance absorbée à vide - pertes joules

P_f = 10,2 - 0,19 = 10,2-0,19= 10 W.

à fréquence constante, les pertes dans le fer sont proportionnelles au carré de la valeur efficace de la tension primaire. Si U₁ est le même à vide et en charge alors les pertes fer sont les mêmes.

Essai n°3 :

courant secondaire de court-circuit, I_2cc= I₁ / m = 0,86 / 0,214 = 4 A.

l'impédance totale ramenée au secondaire, Z_s= mU_1cc / I_2cc = 0,214*8,3 / 4

Z_s= 0,44 W.

Essai en charge nominale :

tension secondaire en charge, V₂ =Z_s I₂ = 11,6*4 = 46,4 V.

résistance R de la bobine : cos j = R/Z doù R = Zcos j = 11,6 * 0,89 = 10,3 W.

puissance active P₂ consommée par cette charge : V₂I₂cos j = 46,4 * 4*0,89 = 165,1 W

rendement du transformateur au cours de cet essai. P₂ / P₁ = 165,1 / 180 = 0,917 ( 91,7%)

pertes par effet Joule du transformateur : P₁ - P₂ - P_f = 180 - 165,1 - 10 = 4,9 W.

valeur de R_s et X_s.

R_s = pertes joule du transformateur / I²₂ = 4,9 / 4² = 0,306 W.

Z²_s = R²_s + X²_s = 0,44² = 0,1936

X²_s = 0,1936 - 0,306² =0,1 d'où X_s = 0,316 W.

retour - menu