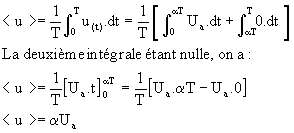Aurélie 06/02
moteur à courant continu, hacheur

STI électrotechnique 00

. .

moteur à courant continu :

Un moteur à courant continu à excitation indépendante fonctionne à flux constant ; son courant inducteur a une intensité ie = 0,35 A. Dans ces conditions, la force électromotrice E peut s'exprimer sous la forme E = k.n, relation dans laquelle n désigne la fréquence de rotation exprimée en tr/min ; on donne k = 0,11 V/tr.min-1. La résistance de l'induit, mesurée à chaud est R= 6,3 W.

  1. Fonctionnement à vide : sous tension d'induit nominal U = 250 V, l'induit absorbe un courant d'intensité I0 = 0,28 A.
    - Calculer la force électromotrice E0 de l'induit dans ces conditions.
    - En déduire la fréquence de rotation n0 du moteur.
    - Evaluer les pertes par effet Joule dans l'induit, notées pJ0.
    - Déterminer le moment Tp du couple de pertes que l'on considérera constant dans la suite du problème.
  2. Fonctionnement en charge : le moteur, toujours alimenté sous tension nominale U = 250 V, développe un couple électromagnétique de moment Te = 2,1 N.m.
    - Montrer que l'induit absorbe alors un courant d'intensité I = 2,0 A.
    - Calculer la force électromotrice E du moteur.
    - En déduire sa fréquence de rotation, n.
    - Le schéma du document-réponse 1, représente le bilan des puissances de l'induit en charge ; en justifiant les calculs effectués, compléter ce schéma en donnant la valeur des différentes puissances mises en jeu.
    - Calculer le rendement de l'induit du moteur en charge.
    - Calculer le moment Tu du couple utile développé par le moteur.

étude du hacheur :

L'induit du moteur étudié dans la partie A est alimenté par un hacheur série dont le schéma est représenté sur la figure 1 ci-dessous. Les interrupteurs électroniques utilisés sont supposés parfaits. Une bobine de lissage, B, de résistance négligeable, est placée en série avec l'induit ; la résistance de celui-ci est il est caractérisé par la relation E = k.n dans laquelle E est exprimée en V et n en tr/min. On donne k = 0,11 V/tr.min-1.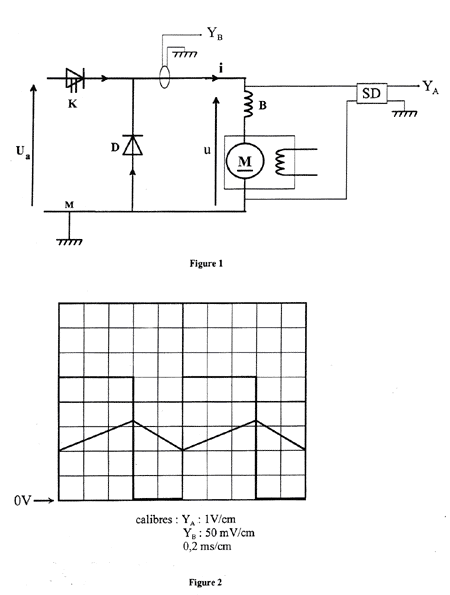

Commande de l'interrupteur K ; T désigne la période de fonctionnement :

0<t<aT : K fermé.

aT <t<T : K ouvert.

En charge, pour un certain régime de fonctionnement, on a relevé à l'oscilloscope les variations de u et i conformément au schéma de la figure 1 ci-dessus. Les oscillogrammes obtenus sont représentés sur la figure 2 ci-dessus. Pour relever ces oscillogrammes on a utilisé une sonde de tension de rapport 1/50 et une sonde de courant de sensibilité 100mV/A.

  1. Déterminer la fréquence de fonctionnement f du hacheur.
  2. Quelle est la valeur du rapport cyclique a le régime étudié ?
  3. < u > désigne la valeur moyenne de la tension aux bornes de l'ensemble moteur + bobine de lissage ; montrer que < u > = 150 V.
  4. Déterminer la valeur maximale IM et la valeur minimale, Im, de l'intensité du courant absorbé par l'induit du moteur.
  5. En déduire l'ondulation Di = IM - Im du courant et sa valeur moyenne < i >.
  6. Ecrire la relation entre < u >, < i >, n, R et k.
  7. Calculer la fréquence de rotation n du moteur
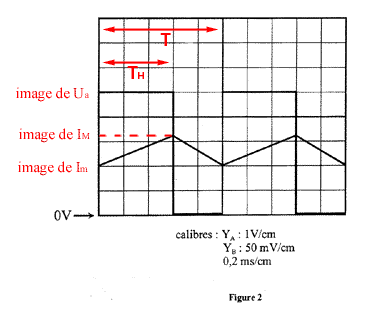
corrigé
le moteur :

Fonctionnement à vide :

U=E0 + RI0 d'où E0 = U-RI0 = 250-6,3*0,28=248 V.

E0 = k n0 d'où n0 = E0 / k = 248/0,11= 2260 tr/min.

pertes par effet joule dans l'induit : Pj0 = RI²0 = 6,3*0,28² = 0,5 W

puissance absorbée = puissance joule + pertes fer + pertes mécaniques

Pa = UI0= Pj0 + Pf +Pm d'où Pf +Pm =UI0- Pj0 =250*0,28-0,5 = 69,5 W.

Couple de pertes : il correspond aux pertes ferromagnétiques et aux pertes mécaniques.

W0 = 2p n0/60 = 6,28*2260/60 = 236,5 rad/s

couple de pertes : G p = (Pm + Pf ) / W0 =69,5 / 236,5 = 0,294 Nm.

Fonctionnement en charge :

Relations fondamentales du moteur à courant continu.

E= K W = kn avec W = 2p n/60 d'où E= K2p n/60 soit K = 60k / (2p )=60*0,11/6,28=1,05

couple électromagnétique : Te = K I = 60k / (2p ) I d'où I = 2p Te/(60k)

I = 6,28*2,11 / (60*0,11) = 2A.

E = U -RI = 250-6,3*2 = 237,4 V.

fréquence de rotation : n = E/k = 237,4 /0,11 = 2158,2 tr/min.

Calcul des diverses puissances.

puissance absorbée : Pa = UI = 250*2 = 500 W

puissance joule : Pj = RI² = 6,3*2² = 25,2 W

* : deux façons de calculer la puissance électromagnétique

Pe = Pa - Pj = 500 - 25,2 = 475 W;

Pe = TeW =Te 2p n/60 = 2,11*6,28*2158,2 / 60 = 476,6 W

Pm + Pf = TpW =Tp2p n/60 =0,294 *6,28*158,2/60 = 66,4 W

* Pu = Pe - (Pf + Pm ) = 476,6 - 66,4 = 410,2W.

Rendement de l'induit : h=Pu/Pa= 410,2 / 500 = 0,82 (82%)

Moment du couple utile :

G u =Pu/W =Pu/ (2p n)*60 = 1,815 Nm.

étude du hacheur:

Sur l'oscillogramme (figure 2), on observe un signal rectangulaire qui correspond à la tension hachée u, et un signal triangulaire correspondant au courant i.

Leurs périodes s'étalent sur 5 carreaux, d'où une période :

T = 5 * base de temps = 5 x 0,2 =1ms = 10-3 s.

et une fréquence de fonctionnement du hacheur :1 / 10-3 = 1000 Hz..

Sur ce même oscillogramme, la durée à l'état haut de la tension u s'étale sur 3 carreaux, comme les durées sont proportionnelles aux longueurs mesurées sur l'oscillogramme, on a : a = TH/T = 3 / 5 = 0,6.

Or, sur l'oscillogramme, l'amplitude de l'image de u (Û=Ua) mesure 5 carreaux soit 5 * 1 = 5V.

On utilise une sonde de tension 1/50, d'où : 5*50 =250 V.

<u>= 0,6*250 = 150 V.

Le signal triangulaire correspond au courant i,

On mesure :

- Valeur maximale : 3,2 carreaux soit une tension égale à 3,2 * 50 = 160mV.

On utilise une sonde de courant de 100mV / A d'où IM = 1,6 A

- Valeur minimale : 2 carreaux : 2*50 = 100mV soit Im = 1A .

Ondulation : Di = 1,6-1 = 0,6 A.

* Valeur moyenne d'un signal triangulaire :

<i>= (IM+Im)/2 = (1,6+1)/2 = 1,3 A.

La loi des mailles permet d'écrire : u = uM+uL

uM est la tension aux bornes du moteur et uL celle aux bornes de l'inductance.

En valeurs moyennes, on obtient : <u >= <uM>+<uL>

or la tension moyenne aux bornes de l'inductance est nulle d'où <u >= <uM> = E + R<i>=kn+ R<i>

n = (<u >-R<i>) /k = (150-6,3*1,3) /0,11 = 1290 tr/min.

retour - menu