Une installation triphasée
équilibrée est alimentée par un
réseau 220V, 380 V, 50 Hz. Chaque fil de phase est
assimilable à un circuit inductif série de
résistance r = 0,6W et
d'inductance L= 1,2 mH. L'installation comporte 30 lampes
à incandescence marquées 100W- 200 V,
également réparties sur les trois phases et
deux moteurs triphasés M1 et M2
dont les caractéristiques nominales sont :
corrigé
les puissances actives des récepteurs s'ajoutent :
30 lampes : 30*100 = 3000 W
M1 : P1 puissance active =
puissance utile / rendement = 4000 /0,8 = 5 000 W
M2 : P1 =3000 /0,85 = 3530 W
puissance active totale : P= 11
530 W.
les puissance réactives s'ajoutent :
les lampes à incandescence ne consomment pas de
puissance réactive
M1 : Q1 = 1,732 UI sin j1
= P1 tanj1
avec j1
=cos-1 0,6 = 53,13° donc Q1 = 6
666,7 var
M2 : Q2 = 1,732 UI sin j2
= P2 tanj2
avec j2
=cos-1 0,7 = 45,6° donc Q2 = 3600
var
total puissance réactive : Q =
10267 var.
puissance apparente S² = P² + Q²
S² = 11530² + 10267² = 2,38 108
soit S = 15440 VA.
facteur de puissance de l'installation : cos j
= P/S =11530/15440 =
0,746.
intensité efficace du courant dans chaque fil de
phase I = S/(1,732 U) = 15440/(1,732*380) =
23,4 A.
impédance de chaque fil : Zl² =
r² + (Lw)² avec
w = 2pf
= 314 rad/s.
Zl² = 0,6² + (1,2
10-3*314)² = 0,5 d'où Z = 0,71
W.
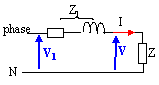
impédance Z = V / I avec V= 380/1,732 = 219,4 V et
I = 23,4A
Z =219,4/ 23,4 = 9,38 ohms
Z+Zl = V1 / I doù
V1 = (0,71+9,38)*23,4 = 236 V soit U1
= 1,732 V1 = 408,8
V.
pertes par effet joule dans un fil : ri² =
0,6*23,4² = 328,5 W
dans les trois fils : 328*3 =
986 W
puissance en début de ligne : Pl =11530
+ 986 = 12516 w
les pertes par effet joule représentent :
986*100/12516 = 8%
on relève le
facteur de puissance :
puissance réactive des condensateurs :
Q1= - 3 Cw U²
Q1= -3 * 35 10-6 *314*380² =
-4760 var
total installation : Q2= 10270-4760 =
5510 var.
puissance active inchangée ( les condensateurs ne
comsomment pas de puissance active) P = 11530 W.
S2² = Q2² + P² =
5510² + 11530² d'où S = 12780 VA
facteur de puissance de l'installation : cos j2
= P/S =11530/12780 =
0,90.
intensité efficace du courant dans chaque fil de
phase I2 = S/(1,732 U) = 12780/(1,732*380) =
19,4 A.
impédance Z = V / I2 avec V= 380/1,732 =
219,4 V et I2 = 19,4,4A
Z =219,4/ 19,4 = 11,3 ohms
Z+Zl = V1 / I2
doù V1 = (0,71+11,3)*19,4 = 233 V soit
U2 = 1,732 V1 =
403,5 V.
pertes par effet joule dans un fil : ri² =
0,6*19,4² = 256 W
dans les trois fils : 226*3 =
678 W
puissance en début de ligne : P2 =11530
+ 678 = 12207 W
les pertes par effet joule représentent :
678*100/12207 = 5,6%
Les pertes par effet joule sont diminuées ;
diminution de la pauissance apparente à fournir en
départ de ligne.
- 3 pompes (Puisance utile 2 kW ; facteur de puissance
0,7; rendement 0,95 et fréquence de rotation n'= 1480
tr/min pour chaque pompe)
-1 broyeur ( Puissance utile 1 kW ; facteur de puissance
0,75 ; rendement 0,9)
-2 pompes (facteur de puissance 0,8 ; fréquence de
rotation n'=2950 tr/min et une puissance absorbé de
1,5 kVA pour chaque pompe )
corrigé
puissance active : P= (racine carrée (3) U I
cos j
Puissance réactive : Q= (racine carrée (3)
U I sin j = P tan j
Puissance apparente ( Pabsorbée) : S =
(racine carrée (3) U I = P/cos j
|
Puissance active(W)
= Putile / rendement
|
Q (var)
|
S( VA)
|
|
pompe n°1
|
2000/0,95=2105
2105*3=6315
|
cos j = 0,7 ;
tan j = 1,02
Q= 2105*1,02=2147
2147*3=6441
|
2105/0,7 = 3007
3*3007=9021
|
|
broyeur
|
1000/0,9=1111
|
cos j = 0,75 ;
tan j = 0,882
Q=
1111*0,882=980
|
1111/0,75=1481
|
|
pompe n°2
|
1500*0,8 =1200
1200*2=2400
|
cos j = 0,8 ;
tan j = 0,75
Q= 1200*0,75 = 900
900*2=1800
|
1500
1500*2
=3000
|
|
total
|
9826
|
9221
|
(P2+Q²)½=13475
|
Intensité :
pompe n°1 : I = P/((racine carrée (3) U cos
j )= 2105/(1,732*380*0,7)= 4,57 A
pour une pompe
Pour les 3 pompes: Iphase = 3*4,57 = 13,71 A
.
broyeur : I = P/((racine carrée (3) U cos
j )= 1111/(1,732*380*0,75)= 2,25
A
pompe n°1 : I = P/((racine carrée (3) U cos
j )= 1200/(1,732*380*0,7)= 2,28 A
pour une pompe
Pour les 2 pompes: Iphase = 2*2,28 = 4,56
A
Intensité totale de phase : 13,71 + 2,25 + 4,56 =
20,52 A.
facteur de puissance de l'installation : P/S= 9826/13475
= 0,73.
retour
- menu