|
|
| .
. |
|
exercice 1 : Trois fils conducteurs rectilignes très longs, parallèles, situés dans le même plan vertical sont parcourus par des courants de même intensité i= 40 A. d1 = 3 cm et d2 = 1cm. 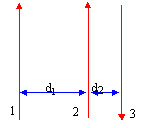
corrigé 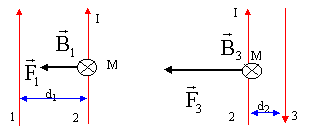
champ crée par le conducteur n°1 en un point M du fil n°2 : perpendiculaire au plan de la figure vers l'arrière B1 = m0 I / (2pd1)= 4*p 10-7 *40 / ( 2p *0,03) = 2,66 10-4 T. force exercée entre les conducteurs n°1 et n°2 : attractive car les courants ont le même sens. F1 = I L B sin (½p)
avec L = 1m d'où F1 = 40*2,66
10-4 = 10,6 10-3 N =
10,6
mN.
B3 = m0 I / (2pd2)= 4*p 10-7 *40 / ( 2p *0,01) = 8 10-4 T. force exercée entre les conducteurs n°3 et n°2 : répulsive car les courants sont de sens contraire. F3 = I L B sin (½p) avec L = 1m d'où F1 = 40*8 10-4 = 32 10-3 N = 32 mN. force totale : 10,6 + 32 = 42,6 mN.
|
|
exercice 2 : Une bobine longue assimilable à un solénoïde est parcourue par un courant i =1 A. Le champ magnétique à l'intérieur de la bobine, mesuré à l'aide d'un teslamètre est B= 11,35 mT. La longueur de la bobine est L= 50 cm
n = B / ( 4*p 10-7 I) = 11,35 10-3 / (4*3,14 10-7 *1) = 9036 spires par mètre soit
4518
spires sur une longueur de 50 cm.
F = N' BS cos 0 =N' B S = 5,8 10-3 Wb d'où N' = 5,8 10-3 / (11,35 10-3 *30,4 10-4) = 168 spires.
retour - menu |