Aurélie 06/02
générateur et récepteur linéaires

fiche cours

. .

générateur:

Un générateur de fem E et de résistance interne r alimente une résistance réglable R.

  1. En fonction de R exprimer :
    - L'intensité du courant dans le circuit.
    - La puissance utile fournie par le générateur.
  2. Etude de la puissance utile en fonction de R :
    - Montrer que lorsque R varie, la puissance utile passe par un maximum pour une valeur particulière de R que l'on précisera.
    - Donner l'expression de la puissance utile maximale en fonction de la valeur de R trouvée précédemment.
    - On donne E=5 V et r=50 ohms calculer la puissance maximale utile, l'intensité du courant, la tension aux bornes du générateur et le rendement électrique du générateur.
  3. Tracer la courbe Pu = f(R) pour R comprise entre 0 et 200 ohms..
  4. La courbe précédente montre que pour une valeur de Pu comprise entre 0 et Pu maximale, il existe deux valeurs de R, notée R1 et R2 de la résistance R.
    - Etablir la relation entre R1, R2 et r.
    - Pour R1=20 ohms, calculer R2 et P . Vérifier sur la courbe..

 

corrigé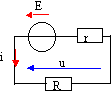

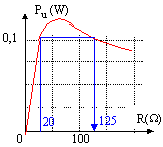
exprimer de deux manières différentes la tension u :

branche contenant le générateur u = E-r i

branche contenant la résistance R : u = Ri

par suite E-r i = R i soit i = E / (R+r).

puissance utile fournie par le générateur : Pu = u i = R i ² = RE² / (R+r)².

dériver P par rapport à R :

rappel : dérivée du quotient (u / v)' = (u' v - v ' u ) / v²

avec u = E²R soit u' = E² et v = (R+r)² soit v ' = 2 (R+r)

P' = E²( r-R) / (R+r)²

cette dérivée est négative pour R >r, nulle pour R=r et positive si R < r.

en conséquence la puissance utile passe par une valeur maximale lorsque R= r

Pu maxi = E² / (4r) = 25/200 = 0,125 W.

intensité du courant si R= r : E /(2r) = 5/100 = 0,05A.

tension aux bornes du générateur si R= r : u = E-r i = 5- 50*0,05 = 2,5 V.

rendement électrique : h = u / E = 2,5/5 = 0,5 (50%).

pour une puissance Pu donnée, inférieure à 0,125 W, il existe deux valeurs correspondantes R1 et R2 de R telles que :

Pu (R+r)² = RE²

Pu R² + 2Pu Rr +Pu r² -RE²=0

R² + (2r -E² / Pu ) R + r² = 0

résoudre cette équation du second degré en R : D = (2r -E² / Pu )² -4r²

le discriminant est positif si Pu < E² / (4r) et le produit des deux solutions R1 et R2 vaut R1R2 = r².

si R1 = 20 W alors R2 = 50*50/20 = 125 W.

Pu = 20*5*5 / (20+50)² = 0,102 W.

moteur :

On associe en série un générateur de fem E = 128 V, de résistance interne r = 0,6 W, une résistance variable R et un moteur de force électromotrice E', de résistance interne r'. Si l'intensité est égale à 4 A, la résistance R vaut 2,5 W. Si l'intensité est égale à 5 A, la résistance R vaut 1 W. Déterminer :

  1. La résistance interne du moteur.
  2. La force électromotrice du moteur
corrigé
tension aux bornes du générateur : u = E-r i

tension aux bornes de la résistance : u1=R i

tension aux bornes du moteur : u2 = E' + r' i

et u = u1 + u2 soit E-r i = R i + E' + r ' i ou E-E' = (R+r+r ' ) i.

128-E' = (2,5 + 0,6 +r ' )*4

32 -E' = 3,1 + r'

28,9 -E' = r '. (1)

128-E' = (1 + 0,6 +r ' )*5

25,6 -E' = 1,6 + r'

24 -E' = r '. (2)

la résolution du systéme constitué par les deux équations (1) et (2) donne : E' = 98 V et r' = 4,4 W.

retour - menu