|
|
|
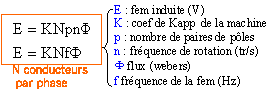
alternateur triphasé : Dans sa zone utile, à la fréquence de rotation de 1200 tr/min, la valeur efficace E de la fem délivrée par un alternateur triphasé est proportionnelle à l'intensité du courant d'excitation par : E= 180 ie.(E en volt et ie en ampère)
corrigé le flux est proportionnel à l'intensité ie : F= k ie.
d'une part E= [ K Np k] n ie. d'autre part E= 180 ie. donc le terme constant [ K Np k] vaut 180 / n avec n = 1200/60 = 20 tr/s ; [ K Np k]= 9 à 1500 trs/min soit n1=1500 / 60 = 25 trs/s : E1 = 9 n1 ie1 = 9*25*0,8 = 180 V.
|
|
alternateur triphasé : Un alternateur triphasé dont les enroulements de l'induit sont couplés en étoile produit, à vide, une tension entre deux bornes U de valeur efficace 2,6 kV et de fréquence f=50 Hz. L'enroulement statorique comporte 2 encoche par pôle et par phase et 12 conducteurs par encoches. Le flux utile sous un pôle est F = 45 mWb. La fréquence de rotation de la roue polaire est n = 500 tr/min
corrigé n = 500 / 60 trs/s np = f d'où p = f/n = 50 *60/500 = 6 paires de pôles soit 2p =12 pôles. nombre de conducteurs par phases : N = 2 *12*2p = 288 conducteurs. couplage étoile : donc la fem E correspond à une tension simple. la valeur relevée entre deux bornes de l'induit correspond à une tension composée en conséquence E = U / ( racine carrée (3 ) = 2600 / 1,732 = 1500 V.
K = E / (NfF ) = 1500 / ( 288*50*0,045) = 2,31. 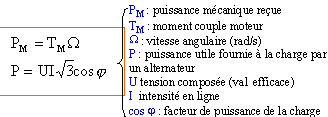
U = P / ( 1,732 I cos j ) = 2,1 106 / (1,732*600*0,9) = 2245 V. rendement h = P / (P+pertes) pertes = P(1-h ) / h = 2,1 106 ( 1-0,85) / 0,85 = 3,7 105 W.
|
|
Les caractéristiques d'un alternateur sont les
suivantes : - expression de la caractéristique à vide Ev = 180 ie( Ev en volt et intensité en ampère) - résistance d'une phase de l'induit r = 0,12 W ; réactance synchrone X= 1,2 W;
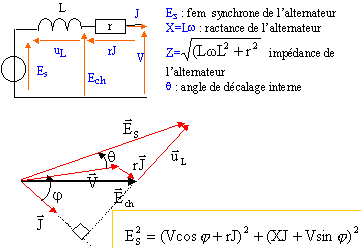
corrigé impédance synchrone Zs: Zs² = X² + r² = 1,2² +0,12² =1,454 d'où Zs= 1,206 W. fem induite en charge :
montage étoile : la tension aux bornes d'une enroulement est 2500 / rac. carrée (3) = 1443,4 V si cos j = 0,8 alors sin j = 0,6 E²s = (1443,4 *0,8 +0,12*400)² + (1,2*400+1443,4 *0,6)² = 3,258 106 d'où Es = 1805 V. puis 1805 = 180 ie d'où ie = 10 A. pertes par effet joule : 3 r i² Pj= 3*0,12*400² = 58 kW. rendement : total des pertes : p = 58+90 = 148 kW puissance mécanique reçue par le moteur : P= UI rac.carrée (3) cos j P = 2500*400*1,732*0,8 = 1385,6 kW h= P / (P+pertes) = 1385,6 / (1385,6+148) = 0,903 (90,3 %)
|
|
moteur synchrone : Un moteur synchrone triphasé, tétrapolaire est alimenté par un réseau triphasé 240V/ 416 V; 50 Hz. Les enroulements du sttor sont couplés en étoile ; la réactance synchrone du moteur est X=8 W ; La fem synchrone du moteur se confond avec sa fem à vide ES= 400 ie. On néglige la résistance de l'induit ainsi que toutes les autres pertes. Le mteur fonctionne à couple constant de moment T= 44 Nm. On se propose de faire varier la puissance réactive absorbée par le moteur en réglant l'intensité d'excitation ie.
corrigé 2p = 4 soit p = 2 paires de pôles np = f soit n = f/p = 50 / 2 = 25 tr/s ou bien 25*60 = 1500 tr/min. puissance active :
P = T W avec W= 2p n/60 = 6,28*1500/60 = 157 rad/s P = 44*157 = 6,9 kW.
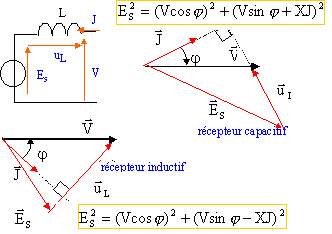
le courant étant en retard sur la tension, le circuit est inductif. cos 37 =0,8 d'où sin 37 = 0,6 ; X= 1,2W ; V = 240 V calcul de I : Pactive = 6900 = UI rac.carrée(3) cos 37 d'où I = 6900 / (416*1,732*0,8) = 11,97 A. puissance réactive : Q1 = UI rac.carrée (3) sin37 = 416*11,97*1,732*0,6= 5,17 kvar. fem synchrone : E²S =(240*0,8)² + (240*0,6 - 8*11,97)² =39191 d'où ES= 198 V. courant d'excitation ie = 198/400= 0,495 A. mêmes calculs avec cos j = 1 et sin j = 1. Pactive = 6900 = UI rac.carrée(3) soit I =6900 / (416*1,732) = 9,57 A. Q1 = 0 E²S =240² + ( 8*9,57)² =6,346 104 d'où ES= 252 V. courant d'excitation ie = 252/400= 0,63 A.
le courant étant en retard sur la tension, le circuit est capacitif. cos 37 =0,8 d'où sin (-37 )= -0,6 ; X= 1,2W ; V = 240 V calcul de I : Pactive = 6900 = UI rac.carrée(3) cos 37 d'où I = 6900 / (416*1,732*0,8) = 11,97 A. puissance réactive : Q1 = UI rac.carrée (3) sin(-37) = -416*11,97*1,732*0,6= -5,17 kvar. fem synchrone : E²S =(240*0,8)² + (240*0,6 + 8*11,97)² =9,446 104 d'où ES= 307 V. courant d'excitation ie = 307/400= 0,767 A.
retour - menu |