. .
|
|
|
|
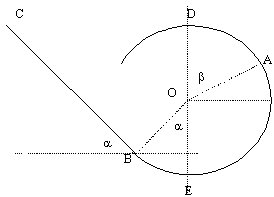
Un solide de masse m se déplace dans une glissière constituée d’une partie rectiligne BC suivie d’une partie circulaire de centre O et de rayon R. Les frottements sont négligés. g=10 ms-2. L’origine des altitudes est le point B. Le solide est lâché de C sans vitesse.
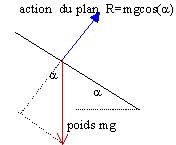
1. Représenter en B et en A les forces appliquées au solide et le vecteur vitesse
2. Exprimer l'énergie mécanique en A et C, puis la vitesse en A en fonction des données
q Calculer la vitesse en A si m=100g R=0,5m BC=2m alpha=1,2 rad béta=1rad
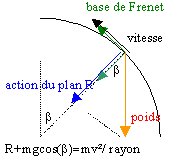
3. La vitesse minimale en D doit être supérieure à
sinon le point D n'est pas atteint. Quelle doit être l'énergie minimale en C permettant d'atteindre D. En déduire l'altitude minimale de C permettant d'atteindre D.
Répondre par Vrai ou Faux .Justifier.
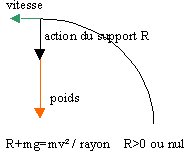
1 En E la somme des forces est nulle.
2 Si la masse quadruple, la vitesse en A double.
3 Si le rayon quadruple, la vitesse en A double.
4 Si la vitesse réelle en A est la moitié de celle calculée, alors 50% de l 'énergie est dissipée sous forme de chaleur lors des frottements
OBcos(a)+OAcos(b)
mgOB(cos(a)+cos(b))
l'énergie mécanique se conserve
vitesse en A
énergie minimale permettant d'atteindre D
E minimale
au point E la vitesse n'est ni constante, ni nulle
seule l'énergie cinétique est divisée par 4
1 compléter
Fe donne Fe3+ +….
NO3- + H+ +..... donne NO(gaz) +….
2 Equilibrer l'équation bilan
3 À 100 mL d'acide nitrique à 0,1 molL-1 on ajoute 0,56 g de fer. Exprimer toutes les quantités de matière en moles.
4 Quel est alors le réactif en défaut ?
5Quelles sont les concentrations de toutes les espèces présentes à la fin.
6 Quel est le volume du gaz.
Masses atomiques molaires en gmol-1 Fe=56 H=1 O=16 N=14 V=22,4 L mol-1
- Fe ® Fe3+ +3 électrons
- NO3- +4 H+ + 3 électrons® NO(gaz) +2H2O
- équation bilan