.. ..
|
|
|
|
fiche : somme des forces - somme des moments des couples
à l'équilibre
la somme vectorielle des forces appliquées au système étudié est nulle
à l'équilibre
la somme algébrique des moments des couples appliqués au solide étudié est nulle
|
|
|
|
|
|
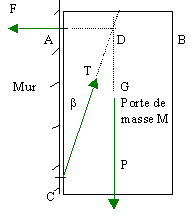
équilibre d'une équerre
La masse M est égale à 10 kg
.et l'angle b =22,8°
- Déterminer l'action du mur en C en écrivant que la somme des moments des couples est nulle à l'équilibre
- Déterminer l'action du mur en A en écrivant que la somme des forces est nulle à l'équilibre
..
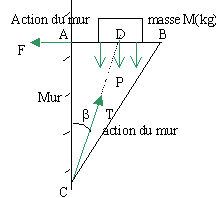
barres AB et BC
forces appliquées à ces barres
actions du mur localisées en B et C
action répartie de la charge M (équivalente à une force unique appliquée en D dans les calculs suivants)
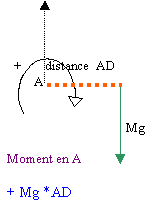
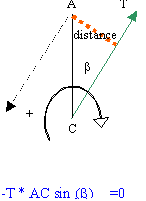
moments en A des couples associés aux forces
somme algébrique des moments
-T AC sin(b) + Mg AD = 0 à l'équilibre
T=105,6 N


F=39,2 N
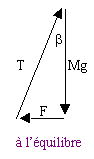
équilibre d'une porte
AD=0,4 m; AC=1,6 m ; AB=0,8 m.
La porte est homogène
- Déterminer l'action du mur en C en écrivant que la somme des moments des couples est nulle à l'équilibre
- Déterminer l'action du mur en A en écrivant que la somme des forces est nulle à l'équilibre
..
la porte
forces appliquées à la porte
actions du mur localisées en A et C
poids de la porte (équivalent à une force unique appliquée en G centre de gravité)
moments en A des couples associés aux forces
somme algébrique des moments
-T AC sin(b) + Mg AD = 0 à l'équilibre
T=202 N
tan(b)=0,4/1,6=0,25 d'où b=14°


F=49 N
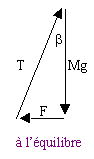
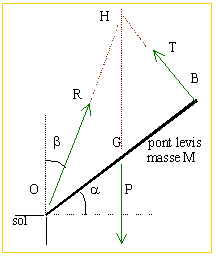
équilibre du pont levis
OB=4 m; OG=2 m ; a=0,4 rad.
Le pont est homogène.
Le cable HB est perpendiculaire au pont
- Déterminer la tension du cable en écrivant que la somme des moments des couples est nulle à l'équilibre
- Déterminer l'action du sol en O en écrivant que la somme des forces est nulle à l'équilibre
.
le pont
forces appliquées au pont
action du sol localisée en O
tension du cable localisée en B
poids du pont (équivalent à une force unique appliquée en G centre de gravité)
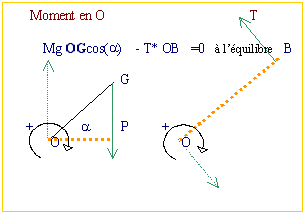
moments en O des couples associés aux forces
somme algébrique des moments
-T OB + Mg OG cos(a) = 0 à l'équilibre
T=451 N
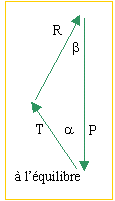
composantes Rx et Ry de l'action du sol en O
Rx -T sin(a)=0 d'où Rx=175,6 N
Ry +Tcos(a) -Mg=0 d'où Ry=564,6 N
tan (b) = Ry / Rx= 3,21 et b=72,7°
R²=Rx²+Ry²; R= 591 N
équilibre d'un panneau
OB=2 m; OG=1 m ; a=0,6 rad.
Le panneau est héterogène.
T est perpendiculaire au pont
- Déterminer T en écrivant que la somme des moments des couples est nulle à l'équilibre
- Déterminer l'action du sol en O en écrivant que la somme des forces est nulle à l'équilibre
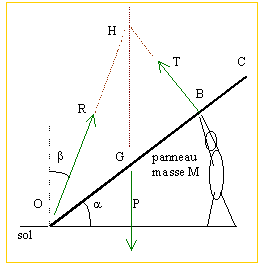
..
le panneau
forces appliquées au panneau
action du sol localisée en O
force musculaire localisée en B
poids du panneau (équivalent à une force unique appliquée en G centre de gravité)
moments en O des couples associés aux forces
somme algébrique des moments
-T OB + Mg OG cos(a) = 0 à l'équilibre
T=202N


Rx -T sin(a)=0 d'où Rx=114 N
Ry +Tcos(a) -Mg=0 d'où Ry=323,3 N
tan (b) = Ry / Rx= 2,83 et b=70,6°
R²=Rx²+Ry²; R= 342 N
levier...le pied de biche
La force F perpendiculaire à OB vaut 10N
- Déterminer l'action du clou en écrivant que la somme des moments des couples est nulle à l'équilibre
- Déterminer l'action du sol en O en écrivant que la somme des forces est nulle à l'équilibre
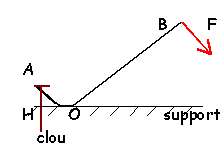
.
le pied de biche
forces appliquées à ce levier
action du sol localisée en O
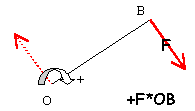
force musculaire localisée en B
action du clou en A
moments en O des couples associés aux forces
somme algébrique des moments
F*OB - R *OH = 0 à l'équilibre
R=80 N
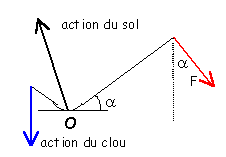
composantes
X etY de l'action du sol
X+F sin(a)=0 d'où X= - 6,4 N
Y -Fcos(a) -R=0 d'où Y=87,6 N
tan (b) = Y / X= -13,7 et b=94,2°
action sol²=X²+Y²;
action sol= 87,8 N
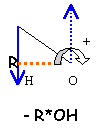
échelle contre un mur solide soumis à 4 forces
|
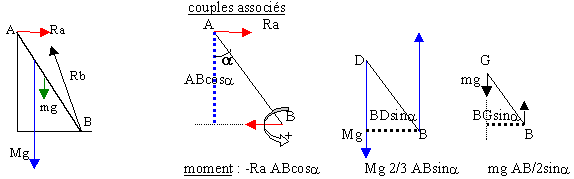
Une échelle simple de 8 kg , de longueur AB=3 m est placée contre un mur lisse (le contact en A,échelle-mur,est sans frottement, action perpendiculaire au mur). L'inclinaison de l'échelle sur la verticale est a=30 degrés. Un individu de masse 60 kg grimpe à l'échelle sur un échelon D tel que AD=1 m. On suppose qu'en B, le contact se fait avec frottements.
|
|
|
|
|
|
|
|
 |
|
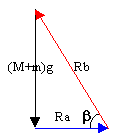
Ra= 249N
b = 69,5 °
Rb²= Ra²+((M+m)g)² .....Rb=711 N
retour - menu