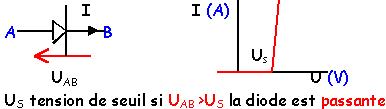physique bac : électricité notions de base lycée
			. .
voir le Quiz : notions de base
rappels	résistors
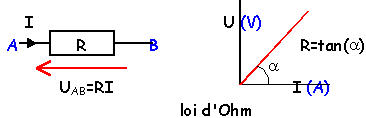
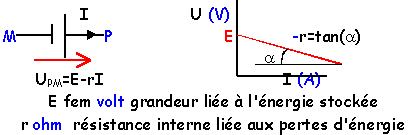
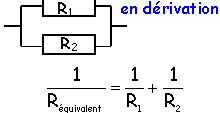
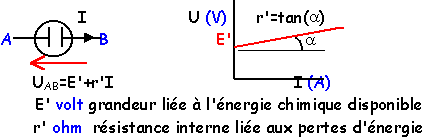
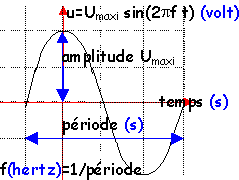
pile ou générateur électrochimique récepteur électrolyseur diode courant alternatif
exercice 1	shunt d'un ampèremètre
Soit un milliampèremètre de résistance 100W . L'intensité maximale qu'il peut supporter est 1 mA. A partir de ce milliampèremètre et d'un shunt (résistance), on désire construire un ampèremètre capable de mesurer des intensités plus importantes. Quelle résistance,S (shunt),faut-il disposer en dérivation aux bornes d'un milliampèremètre pour que l'appareil muni de son shunt ,placé dans un circuit marque 100 quand le circuit est parcouru par uncourant de 1 A? Quelle est alors l'intensité du courant qui traverse le shunt ? Quelle est la résistance R équivalente à l'appareil shunté ? L'appareil shunté précédent est intercalé dans un circuit qui comprend en série une bobine B, dont la résistance est 5 W et la f.c.e.m E'=1,5 volt et un générateur de f.e.m , E et de résistance intérieure r. Les fils de connexion ont une résistance négligeable. L'aiguille de l'ampèrmètre se fixe à la division 50. On remplace la bobine B Par une autre B' ,dont la resistance est alors 10 W (f.c.e.m =1,5 volt ). L'aiguille de l'ampèrmètre se fixe à la division 40. Calculer les valeurs de E et de r. corrigé
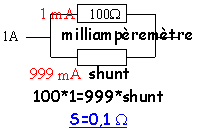résistance équivalente résistances en dérivation : 1/R = 1/100+1/0,1=10,01 R=1/10,01= 0,0999 W loi de Pouillet 0,5=(E-1,5)/(0,1+5+r) 0,4=(E-1,5)/(0,1+10+r) r= 14,9 W ; E=11,5 V
	générateur et électrolyseur
Un générateur est constitué par 20 piles identiques disposées en série . Chaque pile a une f.e.m E= 1V , et une résistance intérieure r = 0,5 ohm On branche ce générateur sur un voltamètre à eau acidulée de résistance 2 W et de f.c.e.m E'= 1,5 volts. Calculer l'intensité du courant . corrigé
n piles en série n piles en dérivation fem équivalente n E E résistance équivalente n r r / n caractéristiques du générateur E = 20*1= 20 V ; r = 0,5*20 = 10 W intensité du courant I= (20-1,5)/(10+2)= 1,54 A
exercice 3	cellules photovoltaiques
Une batterie de cellules photovoltaiques a une surface de 4 m². Son taux de conversion de l'énergie solaire en énergie électrique est de 12%. Elle est installée au Sahel où le rayonnement solaire apporte , en moyenne , 1KJ.m-2 chaque seconde . Quel est le rôle joué par la batterie de cellules photovoltaiques ? Quelle est l'énergie électrique fournie journellement par le convertisseur , pour une durée moyenne d'éclairement de 12 h ? La consommation énergétique journalière d'une famille correspond à la combustion , sans perte , de 1,5 kg de bois . Le pouvoir calorifique du bois est de 13 MJ.kg-1 . Calculer la quantité d'energie correspondante .La comparer avec la valeur obtenue à la question 2. corrigé
La batterie de cellules photovoltaiques est un convertisseur d'énergie Energie électrique fournie chaque jour pendant 12 H (kilojoules) 4*0,12*(3600*12) = 20736 kJ= 20,73 kWh consommation journalière d'énergie (kilojoules) 1 méga joule = 106 joules = 103 kilojoules 1,5*13 103 = 19 500 kJ
exercice 4	vitesse moyenne des électrons dans un fil de cuivre
On veut déterminer la vitesse moyenne v des électrons dans un fil de cuivre cylindrique, de section S=1,0mm², parcouru par un courant d'intensité I=64mA . nombre de masse du cuivre : A=63 ; masse d'un nucléon : 1,7.10-27 Kg ; nombre moyen d'électrons libres par atome de cuivre : k=1,2 ; masse volumique du cuivre : µ= 8900Kg.m-3 ; charge d'un électron (en valeur absolue) : e =1,6.10-19 C . Quelle relation relie v, d distance parcourue par les électrons en 1 seconde ? Quelle relation existe t-il entre t, I et Q quantité d'électrcité ? Quelle relation existe t-il entre Q ,N nombre d'électrons qui traversent la section à chaque seconde, et e, charge élémentaire ? Quelle relation existe t-il entre Q, NA, k? NA : nombre d'atome de cuivre dans le volume de section S et de longueur l. Quel est le nombre d'atomes de cuivre dans le volume S*d ? En déduire la vitesse moyenne des électrons. corrigé
vitesse (ms-1) = distance (m) / durée (s) donc en 1 s :v=d Quantité d'électricité (coulomb)=intensité (A)* durée (s) donc en 1 s :Q=I Q (coulomb)=nombre d'électrons * charge élémentaire (C) donc:Q= N e chaque atome libère en moyenne k=1,2 électrons donc:I=k NA e nombre d'atome de cuivre dans le volume S d volume(m3) * masse volumique (kgm-3)= masse (kg) donc :m =S d r masse d'un atome de cuivre (kg)=masse molaire (kg) / 6,02 1023 donc :0,0635/6,02 1023=1,055 10-25 kg NA=S d r / 1,055 10-25 =10-6 v*8900 /1,055 10-25=8,43 1022v atomes vitesse moyenne des électrons I=k NA e donc 0,064= 1,2*8,43 1022v *1,6 10-19 v = 0,064/ (1,2*8,43*1,6 103)=6,4 10-5/16,18=3,95 10-6 ms-1.
exercice 5	Quelles résistances faut-il choisir ?
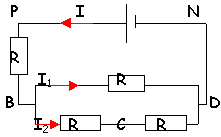
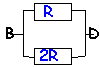
Les résistors sont identiques. Comment choisir les conducteurs ohmiques afin qu'il n'y ait pas de surchauffe? UPN = 12 V ; puissance maximale dissipée par chaque résistor 0,50 W. Exprimer, en fonction de R, la résistance équivalente à l'association des quatre résistors . Exprimer, en fonction de R, l'intensité I du courant principal. Calculer la tension aux bornes de chaque résistor (UPB, UBD, UBC) et vérifier que ces tension sont indépendantes de la valeur de R. Quelle résistor reçoit la plus grande puissance électrique ? Exprimer, en fonction de R, la puissance électrique reçue par le conducteur ohmique situé entre P et B. Quelle valeur minimale faut-il donner à R pour éviter une surchauffe ? On choisit R= 150 W . Calculer l'intensité du courant qui traverse chaque conducteur ohmique. Calculer la puissance reçue par chaque résistor. corrigé
résistance équivalente intensité I :UPN / (5/3R) tension UPB UBD UBC RI=R*UPN/(5/3R)=12*3/5 7,2 V 2/3RI=2/3R*UPN/(5/3R)=12*2/5 4,8 V la moitié de UBD 2,4 V puissance (watt)=tension(volt)*intensité (A) Le résistor situé entre P et B reçoit la plus grande puissance car la tenion à ses bornes est la plus grande et l'intensité qui le traverse est aussi la plus grande. P = 7,2*UPN / (5/3R)= 7,2*12*3/(5R)=51,84/R valeur minimale de R 51,84/R < 0,5 d'où R >51,84/0,5 donc R>104 W. intensité I=12*3/(5*150)= 48 mA I1=4,8/ 150= 32 mA I2=4,8/ 300= 16 mA puissance reçue 7,2*0,048= 0,345 W 4,8*0,032= 0,153 W 2,4* 0,016= 0,038 W
exercice 6	oscillogramme
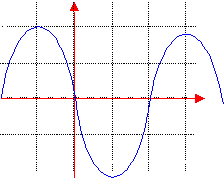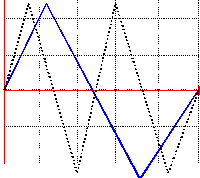
5 V par div et 2 ms par div Déterminer la valeur maximale de la tension observée. Déterminer sa valeur efficace. Déterminer sa période et sa fréquence. On applique sur l'entrée Y d'un oscilloscope une tension en dents de scies symétrique de valeur maximale 5 V de fréquence f = 40 kHz . 2 V par div ; 5 m s par div. Représenter la courbe observée sur l'écran . Avec la même tension , quelle serait l'allure de la courbe si la sensibilité est égale à 10 ms. par div ? On étudie maintenant une tension en créneaux de valeurs extrêmes,4 V et -2 V, de fréquence f = 80 Hz. Qu'observe -t-on dans les deux cas suivants : L'oscilloscope est utilisé sans balayage. L'oscilloscope est utilisé avec le balayage et une sensibilité égale à 5 ms par division. corrigé
amplitude volt tension efficace volt période (s) fréquence (Hz) 2 divisions = 10 10/1,414= 7,07 4 divisions= 0,008 1/0,008= 125 dents de scie crénaux : avec balayage crénaux : sans balayage
exercice 7	associations de résistances et potentiomètre
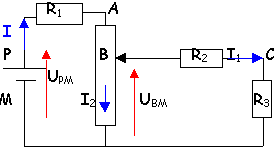Le potentiel de M est nul. UPM=12V. R1=10 W ;R2=10 W; R3=5 W. Le point B est situé au tiers du potentiomètre de résistance totale R=33 W. Quelle est la résistance équivalente R4 à l'association de R2 et R3? Quelle est la résistance équivalente R4 à la portion du potentiomètre comprise entre B et M. Quelle est la résistance équivalente R à tous les résistors du circuit ? Calculer les intensités des courants mA et mA. Calculer la puissance consommée par chaque résistor. corrigé
résistances équivalentes à R2 et R3 en série R4=10+5=15 W. R4 et la portion BM en dérivation 1/15+1/20=7/60 puis 60/7=8,57 W. tout le circuit 8,57 W et 10 W en série 8,57+10= 18,57 W. intensité I=12/18,57 =0,646 A 15 I1 = 20 I2 et I1+I2 = 0,646 I1= 0,278 A et I1= 0,368 A puissance= R I² P1 = 10*0,646²= = 4,17 W P2 = 10*0,278²= = 0,77 W P1 = 10*0,646²= = 0,38 W
exercice 8	charge et décharge d'une batterie
On charge un batterie de voiture pendant t= 10h sous une tension électrique U= 14V avec une intensité électrique I=12A. Rappeler comment doit être branché le chargeur sur la batterie. Calculer la charge Q emmagasinée par la batterie. Calculer l'énergie fournie W par le chargeur à la batterie. Pendant son fonctionnement en générateur,la batterie délivre une intensité l'=13A sous une tension E=12V et elle est déchargée au bout de t'=8h d'utilisation. Calculer W' l'énergie utile restituée par la batterie pendant son uttilisation. Quel est le rendement énergétique de la chaine chargeur batterie? corrigé
Relier la borne positive du chargeur à la borne positive de la batterie. Quantité d'électricité (coulomb)=intensité (A) * temps (seconde) Q=12*10*3600= 4,32 105 coulombs = 120Ah énergie (joule)=Qté électricité (C) * tension (volt) E=4,32 105*14 = 6,05 106 joules =6,05 106/3600 Wh=1,68 kWh énergie restituée par la batterie: 13*12*8*3600= 1,248 kWh rendement= énergie utile*100/ énergie reçue = 1,248*100/1,68 = 74,2%
exercice 9	pile, moteur et résistance en dérivation
E=20V ; R=200 W E'= 16 V r' =10W Quelle est valeur de la tension UAB ? Que vaut l'intensité i1 ? Que vaut l'intensité i ? Quelle est la puissance fournie par le générateur ? Quel est le rendement du moteur ?
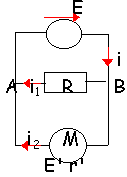
corrigé
UAB = -E = -20 V i1 = UBA / R= 20/200 = 0,1 A calcul de i UBA = E'+r' i2 i2 =(UBA -E' ) / r' = (20-16)/10= 0,4 A i= i1 + i2 = 0 ,5 A puissance (watt) = tension (volt) * intensité (A) puissance fournie par le générateur: 20*0,5= 10 watts rendement moteur = puissance mécanique / puissance reçue puissance reçue par le moteur: 20*0,4 = 8 W puissance mécanique : E' i2 = 16*0,4 = 6,4 W rendement : 6,4/8 *100= 80%
exercice 10 :	batterie : générateur ou récepteur
On utilise une batterie d’accumulateurs pour alimenter une veilleuse dont les caractéristiques sont (5W ; 12V). La résistance interne de la batterie est r = 120 mOhm, sa f.é.m E = 12V et sa capacité est Q = 35Ah.On suppose que la valeur de E reste constante tant que la batterie délivre un courant électrique. Calculer la résistance de la lampe puis calculer l’intensité qui traverse la batterie en fonctionnement. Calculer la durée de l’éclairage de la veilleuse. La batterie complètement déchargée est mise en charge par l’intermédiaire d’un chargeur maintenant une tension U’ = 13,9V à ses bornes. La f.c.é.m de la batterie est alors E’ = 13,2V. Calculer l’intensité I’ du courant électrique passant dans la batterie. Calculer la puissance électrique P’ consommée au cours de cette charge. corrigé puissance de la lampe =UI = RI² = U² / R d'où R =12² / 5 =28,8 ohms intensité I = E / ( somme des résistances) = 12/ (28,8 + 0,12) = 4,15 A durée d'éclairrage Q = It d'où t = 35 / 0,415 = 84 heures la batterie en charge est un récepteur : U' = E' + r I' ; 13,9 = 13,2 + 0,12 I' I' = 0,7/0,12 = 5,8 A puissance consommée par le récepteur : U'I' = 13,9*5,8 =80,6 watts retour - menu - menu