énergie mécanique lycée énergie cinétique (translation) liée à la vitesse proportionnelle à la masse et au carré de la vitesse 0,5 mv² masse en kg, vitesse en ms-1, énergie en joule. (1Wh=3600J)
. .
l'énergie potentielle dépend de l'origine choisie. Par contre la variation de l'énergie potentielle est indépendante de cette origine.
énergie potentielle de pesanteur origine des altitudes : le point le plus bas ou le sol proportionnelle à la masse et à l'altitude mgh masse en kg, altitude en m, énergie en joule. (1Wh=3600J)
énergie potentielle élastique (ressort déformé) origine: la position d'équilibre de l'oscillateur mécanique proportionnelle à la raideur du ressort et au carré de la déformation 0,5 kx² k:raideur en Nm-1, déformation en m, énergie en joule. (1Wh=3600J)
l'énergie mécanique est la somme des énergies cinétique et potentielle. En l'absence de frottement et de force motrice , l'énergie mécanique se conserve.
exercice 1	oscillations d'un pendule
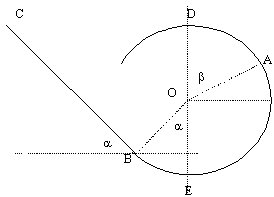
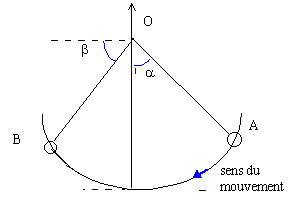
frottements négligeables. Un bille de masse m est suspendue à un fil de masse négligeable. L'origine de l'énergie potentielle de pesanteur est le point le plus bas. m=200 g; OA=0,5 m ; a=0,6rad ; b=1 rad. vitesse initiale en A : 7,2 km h-1. 1 m s-1 =3,6 km h-1. Calculer les altitudes de A et B Calculer l'énergie mécanique en A Calculer la vitesse en B en km h-1. la masse de la bille double, que deviennent l'énergie mécanique ? la vitesse en B ?
corrigé
altitude de A OA(1-cos(a)= 0,0873 m altitude de B OB(1-sin(b)= 0,0793 m énergie mécanique en A somme de l'énergie cinétique et de l'énergie potentielle de pesanteur 0,5 mvA² + mg OA(1-cos(a) danger!!!! vitesse en m s-1 0,571 J
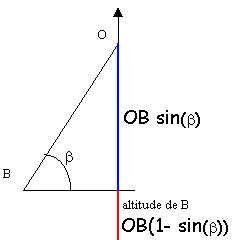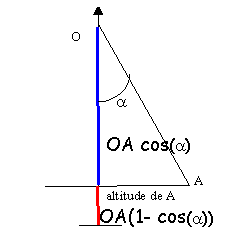
vitesse en B énergie mécanique en B: 0,571 J énergie potentielle en B: 0,2*9,8*0,0793 = 0,155 J énergie cinétique en B: 0,416 J vitesse en B: rac carrée (0,416 *2 / 0,2) 2,04 m s-1 = 2,04*3,6=7,34 km h-1. L'énergie mécanique étant proportionnelle à la masse, si la masse double, alors l'énergie mécanique double. Que devient la vitesse en B si la masse double ? énergie mécanique en A = énergie mécanique en B 0,5mvA²+ mg altitude A = 0,5mvB²+ mg altitude B 0,5vA²+ g altitude A = 0,5vB²+ g altitude B La vitesse en B est indépendante de la masse , vB ne change pas
exercice 2	plan incliné au sommet arrondi
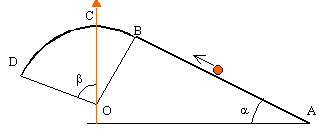
frottements négligeables. Un bille de masse m lancée de A à la vitesse V se déplace vers D. L'origine de l'énergie potentielle de pesanteur est le point le plus bas A. m=1 kg; OB=0,5 m ;AB=2 m ; a=0,3rad ; b=0,9 rad. vitesse initiale en A : 18 km h-1. 1 m s-1 =3,6 km h-1. Calculer les altitudes de B , C et D. Calculer l'énergie mécanique en A Calculer la vitesse en D en km h-1. la vitesse initiale est divisée par deux, que deviennent l'énergie mécanique ? la vitesse en C et en D ?
corrigé
altitude de B hB =AB sin(a)= 0,591 m altitude de C hC =hB+ OB(1-cos(a)= 0,6133 m altitude de D hD =hC -OB(1-cos(b)= 0,424 m énergie mécanique en A entierement sous forme d'énergie cinétique 0,5 mvA² danger!!!! vitesse en m s-1 12,5 J
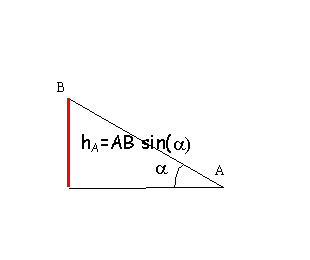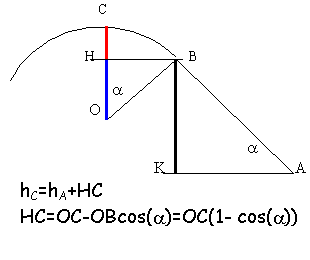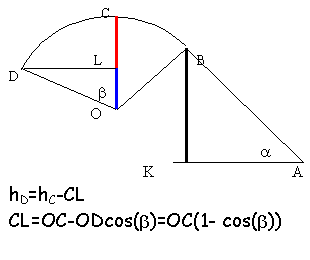
vitesse en D le point D est atteint si on passe en C(sommet) énergie mécanique en C: 12,5 J énergie potentielle en C: 1*9,8*0,6132 = 6 J énergie cinétique en C: 6,5 J on passe au sommet après ça descend énergie potentielle en D: 1*9,8*0,424 = 4,155 J énergie cinétique en D: 8,345 J vitesse en D: rac carrée (8,345 *2 / 1) 4,08 m s-1 = 4,08*3,6=14,7 km h-1. En A l'énergie mécanique est sous forme cinétique, proportionnelle au carré de la vitesse; si la vitesse est divisée par 2, alors l'énergie mécanique est divisée par 4. Que devient la vitesse en D dans ces conditions ? Le point C (sommet) est il atteint ? énergie mécanique en A = énergie mécanique en C 0,5mvA²= 0,5mvC²+ mg altitude C 12,5 / 4 = 0,5mvC²+9,8*0,6132 0,5mvC² =3,125 -6 = -2,87 impossible un carré doit être positif !!!! le sommet C n'est pas atteint, pas plus que D.
exercice 3	descente d'une piste
frottements négligeables. Un bille de masse m lancée de A à la vitesse V se déplace vers M. L'origine de l'énergie potentielle de pesanteur est le point le plus bas O. Le solide décolle après être passé en M. m=1 kg; OB=0,8 m ;AB=2 m ; a=0,1 rad ; b=1,06 rad. vitesse initiale en A : 3,6 km h-1. 1 m s-1 =3,6 km h-1. Calculer les altitudes de A , B et M. Calculer l'énergie mécanique en A Calculer la vitesse en M en km h-1. la vitesse initiale est nulle, que deviennent l'énergie mécanique ? la vitesse en B ?
corrigé
altitude de B hB =OB cos(a)= 0,796 m altitude de M hM = OM sin(b)= 0,698 m altitude de A hA =hB + AB sin(a)= 0,9956 m énergie mécanique en A somme de l'énergie potentielle et de l'énergie cinétique mghA+0,5 mvA² danger!!!! vitesse en m s-1 10,26 J
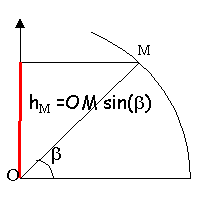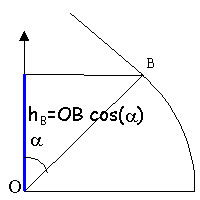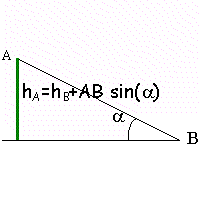
vitesse en M énergie mécanique en M: 10,26 J énergie potentielle en M: 1*9,8*0,698 = 6,84 J énergie cinétique en M: 3,42 J vitesse en M: rac carrée (3,42 *2 / 1) 2,615 m s-1 = 2,615*3,6=9,415 km h-1. En A l'énergie mécanique est sous forme potentielle 9,75 J vitesse en B énergie mécanique en A = énergie mécanique en B 9,75= 0,5mvB²+ mg altitude B 9,75 = 0,5mvB²+9,8*0,796 0,5mvB² =1,95 1,97 m s-1
exercice 4	bille sur une glissière
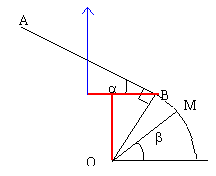
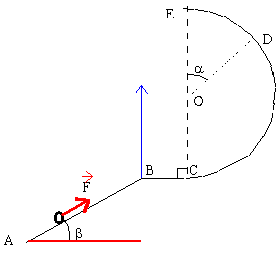
frottements négligeables. Un bille de masse m lancée de A à la vitesse V se déplace vers D. L'origine de l'énergie potentielle de pesanteur est le point A. Une force constante de valeur F=2 N agit entre A et B; l'énergie mécanique en A augmente de F*AB sur le trajet AB. m=100 g; OD=1 m ;AB=2 m ; a=0,5 rad ; b=0,2 rad. vitesse initiale en A : 7,2 km h-1. 1 m s-1 =3,6 km h-1. Calculer les altitudes de B et D. Calculer l'énergie mécanique en A et en B Calculer la vitesse en C puis en D en km h-1. la valeur de F est 0,5 N, que deviennent l'énergie mécanique ? la vitesse en B et D ?
corrigé
altitude de B hB =AB sin(b)= 0,3973 m altitude de D hD= hB+OD(1+ cos(a))= 2,275 m énergie mécanique en A sous forme d'énergie cinétique 0,5 mvA² danger!!!! vitesse en m s-1 0,2 J énergie mécanique en B 0,5 mvA²+F*AB= 4,2 J
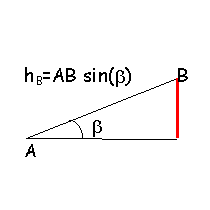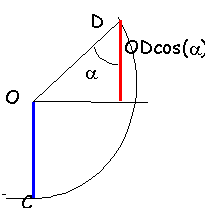
vitesse en C = vitesse en B (aucune force ne travaille entre B et C ) énergie mécanique en C: 4,2 J énergie potentielle en C: 0,1*9,8*0,3973 = 0,389 J énergie cinétique en C: 3,811 J vitesse en C: rac carrée (3,811 *2 / 0, 1) 8,73 m s-1 = 8,73*3,6=31,43 km h-1. énergie mécanique en D: 4,2 J énergie potentielle en D: 0,1*9,8*2,275 = 2,23 J énergie cinétique en D: 1,97 J vitesse en D: rac carrée (1,97*2 / 0, 1) 6,28 m s-1 = 6,28*3,6=22,6 km h-1. En B l'énergie mécanique vaut : 1,2 J vitesse en B 1,2 = 0,5mvB²+ mg altitude B 1,2 = 0,5mvB²+0,1*9,8*0,3973= 4 m s-1 En D l'énergie mécanique vaut : 1,2 J vitesse en D 1,2 = 0,5mvD²+ mg altitude D 1,2 = 0,5mvB²+0,1*9,8*2,275 le calcul conduit à une valeur négative pour 0,5mvB² ; D ne peut être atteint
exercice 5	énergie, puissance, frottements
Pour faire rouler une voiture pendant une minute,à la vitesse constante 90km/h,son moteur reçoit une énergie de 4,8 MJ qui provient de la combustion de l'essence. Le rendement du moteur est de 30%. La combustion d'un litre d'essence fournit 35 MJ. La route est horizontale. Calculer l'énergie mécanique fournie par le moteur considéré pendant une minute. En déduire la puissance mécanique moyenne. Calculer la valeur des forces de frottements supposées constantes. Quelle sera la consommation pour parcourir 100 km à la vitesse indiquée. corrigé énergie mécanique : 4,8*0,3 = 1,44 106 J puissance (watt) = énergie mécanique (joule) / durée (seconde) P = 1,44 106 / 60 = 24 kW La puissance mécanique mise en jeu est utilisée pour compenser la puissance perdue lors des frottements avec la route . Force motrice et force de frottements sont opposées. puissance (watt) = force motrice (N) * vitesse (ms-1). vitesse =90/3,6=25 ms-1....F = 24 000 / 25 = 960 N. consommation à chaque minute : 4,8 / 35 = 0,137 L en 60 s on parcourt 60*25 = 1500 m consommation aux 100 km: 0,137*100/1,5 = 9,13 L
exercice 6	looping
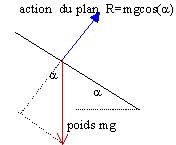
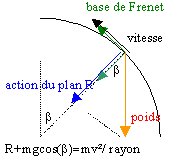
Un solide de masse m se déplace dans une glissière constituée d’une partie rectiligne BC suivie d’une partie circulaire de centre O et de rayon R. Les frottements sont négligés. g=10 ms-2. L’origine des altitudes est le point B. Le solide est lâché de C sans vitesse. 1. Représenter en B et en A les forces appliquées au solide et le vecteur vitesse 2. Exprimer l'énergie mécanique en A et C, puis la vitesse en A en fonction des données q Calculer la vitesse en A si m=100g R=0,5m BC=2m a =1,2 rad ; a =1rad 3. La vitesse minimale en D doit être supérieure à racine carrée (10*R) sinon le point D n'est pas atteint. Quelle doit être l'énergie minimale en C permettant d'atteindre D. En déduire l'altitude minimale de C permettant d'atteindre D. Répondre par Vrai ou Faux .Justifier. 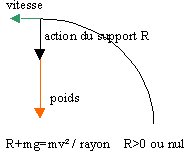1 .En E la somme des forces est nulle. 2 .Si la masse quadruple, la vitesse en A double. 3 .Si le rayon quadruple, la vitesse en A double. 4 .Si la vitesse réelle en A est la moitié de celle calculée, alors 50% de l 'énergie est dissipée sous forme de chaleur lors des frottements corrigé au point C au point A au point D altitude BC sin(a) OBcos(a)+OAcos(b) OBcos(a)+OA Energie potentielle mgBC sin(a) mgOB(cos(a)+cos(b)) mgOB(cos(a)+1) Energie cinétique 0 0,5 m Va2 0,5 m Vd2 forces l'énergie mécanique se conserve Va²=2g(BC sin(a)-OB(cos(a)+cos(b))) vitesse en A : 5,3 ms-1 énergie minimale permettant d'atteindre D mgOB(cos(a)+1)+0,5 m Vd2  avec Vd2=gOB 0,93 J tout est faux au point E la vitesse n'est ni constante, ni nulle : donc la somme des forces n'est pas nulle dans l'expression de la vitesse la masse ne figure pas la vitesse n'est pas proportionnelle à la racine carrée du rayon OB seule l'énergie cinétique est divisée par 4 alors que l'énergie potentielle ne change pas retour - menu