Equilibre thermodynamique des fluides Fuite isotherme d'un gaz Détecteur d'incendie Principe d'un densimètre Mongolfière Force pressante sur un barrage obturateur prismatique En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . .

Fuite isotherme d'un gaz : Un récipient de volume V= 100 L contient du dioxygène à la température T= 300 K , gaz assimilé à un gaz parfait. La température du récipient est maintenue constante. Le récipient est percé d'un petit trou de section s = 1 mm². L'orifice donne sur un second récipient où le vide est maintenu. Le module moyen de la vitesse à la température T est <v>=445 m/s. Donner l'évolution de la pression en fonction du temps ? Quelle est la constante de temps du phénomène ? corrigé Le petit trou ne perturbe guère l'équilibre thermodynamique du gaz dans le récipient et l'équation d'état s'écrit : PV=nRT = N /NA R T = N kB T (1) P : pression en pascal ; V : volume en m3 ; n : Qté de matière en mol ; T : température en kelvin ; R= 8,31 J mol-1 K-1. N : nombre de particules ( molécules O2) ; NA : nombre d'Avogadro ; kB=R/NA : constante de Boltzmann. La température et le volume restent constant : la dérivée logarithmique de (1) donne : dP/P = dN/N La variation relative de la pression est égale à la variation relative du nombre de particules contenues dans le récipient. Soit dN le nombre de particules sortant du récipient pendant la durée dt à la vitesse v faisant un angle q avec un axe Oz perpendiculaire à la section du trou; dN est égal au nombre de particules contenues dans un volume svdt , de section s et de longueur v dt. dans le volume V, il y a N particules ; dans le volume svdt il y a N/V*svdt particules d N = N/V s vdt cos q. moyenne statistique : <dN >= Ns dt /V < v cosq> Le module de la vitesse v est une variable statistique variant de 0 à l'infini ; quand à l'angle q il varie de 0 à ½p. 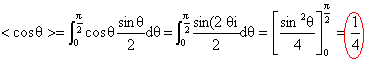d N= 0,25 N/V s <v> dt le nombre de particules sortant est l'opposé de la diminution (notée dN) du nombre de particules dans le récipient : dN= -d N= -0,25 N/V s <v> dt Or dP/P = dN/N = -0,25 /V s <v> dt la constante de temps du phénomène est t = V / (0,25 s <v>) d'où : dP/P = - t -1dt primitive de dP / P : ln P ; primitive de dt : t à une constante près par intégration entre P0 et P et entre 0 et t : ln(P/P0) = - t -1t ou bien P = P0 exp(- t -1t). application numérique : t = 0,1 /(0,25 10-6*445)= 900s, ou 15 min.

Détecteur d'incendie Une petite quantité d'eau liquide, à une température T et sous une pression P possède un coefficient de dilatation isobare a=3 10-4 K-1 et un coefficient de compressibilité isotherme C= 5 10-10 Pa-1 ; ces coeficients sont constants dans les domaines de température et de pression étudiés. Volume massique de l'eau sous 1 bar à 273 K : v0=10-3 m3 kg-1. Le volume massique de l'eau varie peu en fonction de la pression et de la température ; calculer sa valeur à 293K sous 1000 bar. Donner une valeur approchée du volume massique en fonction de la température et de la pression. L'eau étudiée est enfermée dans un récipient métallique de volume constant qu'elle remplit totalement, à 293 K sous 1 bar. Un incendie échauffe le récipient jusqu'à la température T2=586 K sous une pression P2. Calculer P2. - Quelle aurait été la pression P3 d'un gaz parfait à la place de l'eau ? Les dispositifs de protection contre l'incendie utilisent cette propriété. Une ampoule en verre de silice est entièrement remplie par de l'éthanol de sorte que sous un bar et à 67°C l'ampoule soit entièrement remplie par le liquide. Si la température atteint 68 °C, elle se brise, libérant la vanne d'une conduite d'eau sous pression. Quel est l'avantage de l'éthanol sur l'eau dans ce dispositif ? Pour l'éthanol : a=1,8 10-4 K-1 et C= 4 10-11 Pa-1 ; corrigé définition du coefficient de compressibilité isotherme : C= -1/v (dv/dP)T. Le volume varie peu donc v voisin v0 ; de plus on confond la tangente en M à une courbe à la corde MM', avec M' proche de M soit (dv/dP)T = (Dv/DP)T. Par suite : C= -1/v0 (Dv/DP)T = -1/v0 (v-v0)/(P-P0) d'où v-v0 = -Cv0(P-P0) ou v = v0 (1-C(P-P0)). v =10-3 (1-5 10-10*(1000-1)105)= 0,95 10-3 m3 kg-1. volume massique en fonction de la température et de la pression : (dv/dP)T = -Cv0 soit à T =constante : dv = -Cv0 dP intégration : v = -Cv0 P + f(T) avec f(T) une constante pour la pression, mais dépendant de la température. déterminons f(T) à partir du coefficient de dilatation isobare a = 1/v (dv/dT)P. soit (dv/dT)P voisin de a v0 or (dv/dT)P = f '(T) soit en intégrant : f(T) = a v0 T + cte ; puis v = -Cv0 P + a v0 T + cte calcul de la constante : v(T0, P0)= v0= -Cv0 P0 + a v0 T0 + cte cte = v0(1+C P0-a T0) puis v = v0 [-C (P0-P) + a (T - T0)+1].(1) Le récipient a un volume constant : si T augmente le volume massique du liquide ne peut donc pas augmenter. (1) donne : -C (P0-P2) + a (T2 - T0)=0 soit P0-P2= a / C (T2 - T0) P2= P0+a / C (T2 - T0) = 105+3 10-4 / ( 5 10-10 ) * (586-293)= 1758 bar. Le récipient se fendra ou explosera bien avant que la pression n'atteigne cette valeur. Dans le cas d'un gaz parfait : PV= nRT avec n = masse (kg) / masse molaire M(kg/mol) PV= m/M RT soit le volume massique : v= V/m = RT / (PM) si la température double ( 583 voisin de 2*293), v restant constant alors la pression double. P3 = 2 bar et le récipient ne se casse pas. en remplaçant l'eau par l'éthanol : P2= P0+a / C (T2 - T0) donne a / C =( P2- P0) / (T2 - T0) pour l'eau : a / C =3 10-4 / ( 5 10-10 )= 6 105 ; pour l'éthanol : a / C =1,8 10-4 / ( 4 10-11 )= 4,5 106 soit 7,5 fois plus grand que dans le cas de l'eau La pression augmente 7,5 fois plus vite dans le cas de l'éthanol ( par rapport à l'eau) : le déclenchement de la protection sera donc plus précis.

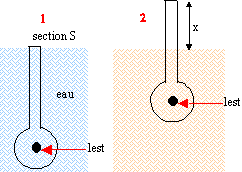
Principe d'un densimètre V : volume total du densimètre ; S : section de la partie cylindrique. Plongé dans l'eau de masse volumique re, il affleure (1); par contre dans un liquide de masse volumique r >re, il occupe la position (2). Exprimer la densité du liquide en fonction de S, x et V. corrigé Le densimètre est en équilibre sous l'action de son poids, vertical vers le bas et de la poussée d'Archimède, verticale vers le haut, de valeur égale au poids du volume de liquide déplacé. dans l'eau : mg = V re g Dans un liquide de masse volumique r >re : mg = (V-Sx)r g par suite : V re g = (V-Sx)r g soit r/ re = V / (V-Sx) La densité d'un liquide par rapport à l'eau est égale au rapport des masses volumiques d =r/ re ; d =V / (V-Sx).

Mongolfière Une mongolfière est constituée d'une enveloppe de volume V=2000 m3 gonflée à l'air chauffé à T=100 °C. La masse de l'enveloppe pliée, de la nacelle, accessoires et passager est m = 200 kg. La température de l'air à l'intérieur de l'enveloppe est maintenue constante gràce à un brûleur. La mongolfière est solidement amarrée au sol jusqu'au remplissage complet de l'enveloppe. Quelle est la valeur de la force ascensionnelle au décollage ? Les gaz sont supposés parfaits ; masse molaire de l'air M=29g/mol. La température de l'atmosphère et T0=20°C et la pression est P0=1 bar au niveau du sol. Quelle est l'altitude maximale atteinte si l'atmosphère est en équilibre isotherme ? corrigé masse totale au décollage = masse de la mongolfière m + masse de l'air chaud notée mair chaud = rair chaud V rair est la masse volumique de l'air chaud , V le volume de l'enveloppe. Les amarres étant rompues, la mongolfière est soumise à son poids P, verticale, vers le bas, et à la poussée d'Archimède P , verticale vers le haut.. La résultante de ces deux forces constitue la force ascensionnelle F, verticale vers le haut. Le volume d'air déplacé est pratiquement égal à V d'où P = rair extérieur V g Le poids est P= (m+mchaud)g d'où F = ( rair extérieurV -(m+mair chaud))g exprimons ( rair extérieurV -(m+mair chaud)) en fonction de P0, V, R , T, T0 et M équation d'état des gaz parfaits : PV=nRT avec n = mair chaud /M P0V = mair ext /M RT0 soit P0=mair ext /V *RT0 /M = rair extérieur RT0 /M soit rair extérieur = P0M/(RT0) de même Pintérieur=rair chaud RT /M soit rair chaud = P0 M/(RT) (la pression intérieure est égale à la pression de l'air extérieur ) par suite : rair extérieurV -m-mair chaud= rair extérieurV - m-rair chaud V =(rair extérieur -rair chaud )V -m soit P0MR-1 V ( 1/T0 -1/T )-m et F= [P0MR-1 V ( 1/T0 -1/T )-m]g. calcul : F=(105*29 10-3/8,31*2 103(1/293-1/373)-200)*9,81=((6,98 105*7,29 10-4)-200)*9,81=3030 N. Lors de l'ascension la pression diminue alors que tous les autres paramètres restent constants ; en conséquence la force ascensionnelle diminue et la mongolfière ne monte plus lorsque F=0 PMR-1 V ( 1/T0 -1/T )= m P= mR/(MV)( 1/T0 -1/T )-1. Il faut établir l'expression de la pression en fonction de l'altitude h par rapport au sol. équation de la statique des fluides : dP/dh = -rg. équation des gaz parfaits : P=rRT/M soit r = PM/(RT) par suite dP/dh = -gPM/(RT) ou encore : dP/P=-gM/(RT) dh intégration : ln P = -gM/(RT) h + cte au sol P=P0 et h=0 d'où : cte =lnP0 et ln (P/P0 ) = -gM/(RT) h ; P = P0 exp(-gM/(RT) h). égalons les deux expressions de la pression P : mR/(MV)( 1/T0 -1/T )-1=P0 exp(-gM/(RT) hmaxi). -gM/(RT) hmaxi= ln[mR/(MVP0)( 1/T0 -1/T )-1] hmaxi= -RT/(gM) ln[mR/(MVP0)( 1/T0 -1/T )-1] hmaxi=RT/(gM) ln[MVP0( 1/T0 -1/T )/(mR)] calcul : RT / (gM) = 8,31*293 /(9,81*29 10-3)=8,56 103. MVP0( 1/T0 -1/T )/(mR) =29 10-3 *2 103*105(1/293-1/373) /(200*8,31)=2,544 ln 2,544 = 0,933 ; hmaxi = 8,56 103 * 0,933 = 7986 m.

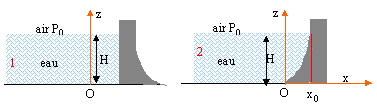
Force pressante sur un barrage Le barrage est un mur vertical (1) de largeur L. Déterminer la force exercée par l'eau sur le barrage Le barrage a un profil parabolique (2) tel que z =x²/h de largeur L. Déterminer la force exercée par l'eau sur le barrage. - Fx et Fz dépendent-elles de x ? corrigé pression dans l'eau à l'altitude z : équation d'équilibre d'un fluide incompressible : dP/dz = -rg intégration : P = -rgz + Cte. à z=H la pression vaut P0 : P0= -rgH + Cte ; d'où la constante : P0+rgH par suite P= P0+rg(H-z) Force pressante sur le mur : On considère une petite bande de longueur L, de hauteur dz, comprise entre la cote z et la cote z+dz. Aire de cette bande :dS= Ldz ; la pression est uniforme sur cette petite bande. La force exercée par l'eau sur cette bande est dirigée suivant Ox et vaut : dFx= P dS dFx= (P0+rg(H-z))Ldz = L( P0+rgH)dz -rgL zdz intégration entre z=0 et z=H : Fx=[ L( P0+rgH)z]0H-½rgL z²]0H = P0LH +½rgH². dans le second cas : P= P0+rg(H-z) On utilise la même méthode, mais la surface est inclinée par rapport à la verticale: la projection de cette surface sur la verticale est dS=Ldz et le calcul de la force Fx est identique à la question précédente. Projection de cette surface sur l'horizontale : Ldx et la force pressante dFz est perpendiculaire à cette surface, dirigée de l'eau vers le fond du barrage, donc en sens contraire de l'axe z. dFz = -P Ldx = -( P0+rg(H-z))Ldx avec z=x2/h dFz =  -( P0+rg(H-x2/h))Ldx intégration entre 0 et x0 : Fz = -L[(P0+ rgH)x -rgx3/(3h)]0x0 = -L[(P0+ rgH)x0 -rgx03/(3h)] Or H = x0²/h d'où Fz = -L[P0x0+2rgx03/(3h)]. cette valeur dépend de la forme du pofil du barrage.

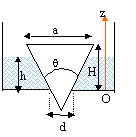
Obturateur prismatique Le fond d'un récipient présente une ouverture rectangulaire de longueur L, de largeur d. Un obturateur en forme de prisme isocèle, de longueur L, de masse m est introduit dans l'orifice. Un joint d'épaisseur négligeable assure l'étanchéité. Exprimer la résultante des forces pressantes sur le prisme dans le cas où h<H, puis dans le cas où h>H. - A quelle condition l'obturation est-elle garantie quelle sue soit la quantité d'eau versée ? corrigé pression dans l'eau à l'altitude z : la pression de l'air au dessus du liquide vaut P0. équation d'équilibre d'un fluide incompressible : dP/dz = -rg intégration : P = -rgz + Cte. à z=H la pression vaut P0 : P0= -rgh + Cte ; d'où la constante : P0+rgh par suite P= P0+rg(h-z) d'où la pression efficace due à l'eau est : P- P0= rg(h-z) la pression efficace due à l'air est nulle. 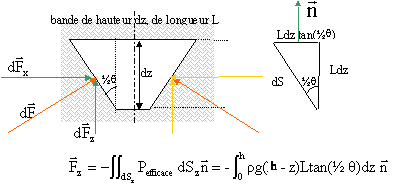Le prisme est symétrique par rapport à deux plans verticaux perpendiculaires : on choisit des éléments de surface symétriques par rapport à ces deux plans : dans ce cas les composantes horizontales des forces de pression sur les faces obliques se compensent. sur les faces obliques on considère des bandes comprises entre les cotes z et z+dz, de surface dS avec dSz=Ldz tan(½q) ; les faces verticales ne contribuent pas à Fz. si h<H : la composante verticale des forces pressantes est : Fz = rgLtan(½q)[hz-½z2]0h = ½rgLtan(½q)h2 sur chaque face oblique, soit pour les deux faces : rgLtan(½q)h2. la force pressante Fz croît avec h , sa valeur maximale est : rgLtan(½q)H2 si h>H : force pressante Fz sur une face oblique : calcul identique mais intégrer entre 0 et H Fz = rgLtan(½q)[hz-½z2]0H =rgLtan(½q)H(h-½H) pour les deux faces obliques : rgLtan(½q)H(2h-H) force pressante sur la face supérieure (d'aire aL ) verticale, en sens contraire de l'axe z : -rg(h-H)aL Fz totale = rgLtan(½q)H(2h-H) -rg(h-H)aL or tan(½q) = (a-d) / (2H) Fz totale = rgL(½(a-d)(2h-H)-(h-H)a) =½rgL(aH-d(2h-H)). cette force décroît avec h ; sa valeur maximale est :½rgLH(a-d) Le récipient est fermé, sans fuite, si le poids mg est supérieur à la la valeur maximale de la force pressante mg>½rgLH(a-d) soit m>½rLH(a-d). retour - menu