![]() résonance
et antirésonance d'après
ENAC
résonance
et antirésonance d'après
ENAC
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
| .
. |
| .
. |
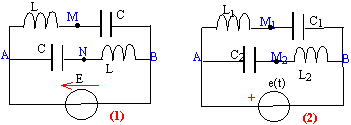
E= 20 V ; L= 2 mH ; C=0,2 mF ; à l'instant initial où l'on applique la tension E, bobine et condensateur ne stockent aucune énergie.
- Donner l'expression de la charge q d'un condensteur
en fonction du temps (fig 1).
- Donner l'expression de la tension aux bornes d'un condensateur, notée uC(t).
- Donner l'expression de vM-vN.
- En déduire sa valeur maximale. - Figure 2 : amplitude de la tension e(t) :
E=20 V ; Bobines et condensateurs ne sont pas
identiques.
- Le courant de pulsation w1 tel que L1C1w12 = 1, traverse-t-il le circuit ?
- Même question avec w2 tel que L2C2w22 = 1. - Pour quelle pulsation w3
obtient -on un circuit bouchon ?.
- Calculer la fréquence N3 correspondant à w3 pour L1=2 mH, L2 = 1 mH, C1= 1mF et C2 = 0,02 m F. - A la fréquence N3, quelle est
l'amplitude de l'intensité du courant I (mA)
circulant dans les branches AM1B et
AM2B ?
corrigé
Le générateur de tension est idéal , on écrit la loi des mailles dans chaque branche :
E=uC(t) + Ldi/dt avec q(t) = CuC(t) et i(t) = dq /dt = CduC/dt ; di/dt = d2q /dt 2= Cd2uC/dt 2
d'où l'équation différentielle régissant la charge q(t) :
E = q(t) / C +L d2q /dt 2
CE = q(t) + LC q"(t) .(1)
solution générale de (1) = solution particulière de (1) + solution générale de 0= q(t) + LC q"(t) .
solution particulière de (1) : q= CE
solution générale de q(t) + LC q"(t) =0 : q(t) = A cos (wt+j) avec w=(LC)-½ = (2 10-3 * 2 10-7)-½= 5 104 rad/s.
solution générale de (1) : q(t) = A cos (wt+j) +CE
i(t) = -Aw sin (wt+j) ; à l'instant t=0, i=0 d'où 0 =-Aw sinj soit j=0 ou j=p.
à t=0 , la charge q est nulle : 0= A cosj +CE soit A = -CE si j= 0 ou A=CE avec j= p.
q(t) = -CE cos (wt)+CE = CE(1-cos (wt)).
avec CE= 2 10-7*20= 4 10-6 coulomb.
uC(t) = q(t) / C= E(1-cos (wt)).
la tension est maximale si cos
(wt)
= -1 et vaut 2E= 40
V.
vM-vN=
vM-vA+vA-vN
le courant va de A vers M : vA-vM= Ldi/dt et vM-vA= -Ldi/dt
le courant va de A vers M : vA-vN= uC(t)
vM-vN= -Ldi/dt + uC(t) = -LCd2uC/dt 2 + uC(t)
uC(t) = E(1-cos (wt)) ; u'C(t) = Ew sin (wt) ; u"C(t) = Ew2 cos (wt) ;
vM-vN= -LCEw2 cos (wt) +E(1-cos (wt)) vec LCw2 =1
vM-vN=E(1-2cos (wt)).
valeur maximale si cos
(wt)
= -1 soit
3E=60V.
impédance complexe de la branche 1 :
z1=j[L1w
- 1/(C1w)]
intensité complexe i1 = E / z1= E / [j(L1w - 1/(C1w))]
impédance complexe de la branche 2 : z2=j[L2w - 1/(C2w)]
intensité complexe i2 = E / z2= E / [j(L2w - 1/(C2w))]
intensité complexe dans la branche de la source i = i1 + i2
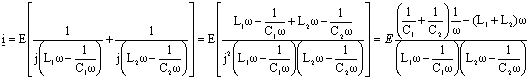
si w tend vers w1 ou vers w 2 le dénominateur tend vers zéro et l'intensité tend vers l'infini.
par contre l'intensité est nulle si le numérateur est nul soit :
w 32=1/(L1+L2) [1/C1+1/C2]
fréquence N3 correspondant à w 3 :
w 32= 103 / 3 *106[1/1+1/0,02]=1,7 1010.
w 3 = 1,3 105 rad/s d'où N3 = 1,3 105 / (2p) =2,07 104 Hz = 20,7 kHz.
w 12= 1/(L1C1)=109 / 2 =5 108.
w 1 = 2,23 104 rad/s d'où N1 = 2,23 104 / (2p) =3,55 103 Hz = 3,55 kHz.
w 22= 1/(L2C2)=109 / 0,02 =5 1010.
w 2 = 2,23 105 rad/s d'où N2 = 2,23 105 / (2p) =3,55 104 Hz = 35,5 kHz.
N3 est comprise entre N1 et N2.
intensité dans chaque branche si N=N3.
i1 = E / [j(L1w 3 - 1/(C1w 3))]
module de i1 : E/[(L1w 3 - 1/(C1w 3))]=20 / (260-7,7) = 0,079A = 79 mA.
i1 +i2 = 0 soit i1 = -i2 .
Les deux nombres complexes i1 et i2 sont opposés : ils ont même module mais leurs arguments sont opposés.
Les intensités ont même module mais sont en opposition de phase ( circuit bouchon).
retour - menu