réponse d'un filtre actif à un signal sinusoïdal à un signal triangulaire En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . .

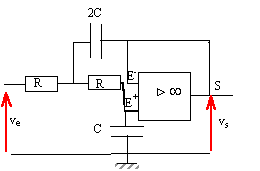
étude en régime permanent sinusoïdal L'amplificateur opérationnel est supposé idéal et fonctionne en régime linéaire La tension d'entrée est : ve=Em cos(wt) avec Em la valeur maximale et w la pulsation. La tension de sortie est notée vs = Vm cos (wt+j) avec Vm la valeur maximale et j le déphasage de cette tension par rapport à la tension d'entrée. Quel est la nature du circuit électronique proposé. - Montrer que la fonction de transfert peut s'écrire : H(jw) = vs / ve= [1+2jRCw-2(RC)²w²]-1. - Exprimer en fonction de R, C et w la gain du filtre noté G(w), le déphasage j. Ecrire la fonction de transfert sous la forme : H(jw) = vs / ve= [1+2js w/w0-(w/ w0)²]-1. Exprimer les constantes s ( coefficient d'amortissement du filtre) et w0 en fonction de R et de C. Quel est la la nature du filtre. Définir le gain exprimé en décibels (dB), noté dans la suite GdB. Déterminer le comportement asymptotique du gain en décibels, c'est à dire l'expression simplifiée de GdB pour w <<w0 et w >>w0. Dans la suite on considèrera que w <<w0 si w <w0/10 et que w >>w0 si w >10 w0. Application numérique : C= 1mF et R=100 W. - Calculer w0. - Tracer le diagramme de Bode en amplitude du filtre, w variant entre 102 et 106 rad/s. - Définir puis calculer la bande passante du filtre. corrigé à très basse fréquence, un condensateur se comporte comme un coupe-circuit à très haute fréquence, un condensateur se comporte comme un court-circuit le filtre est un passe-bas. 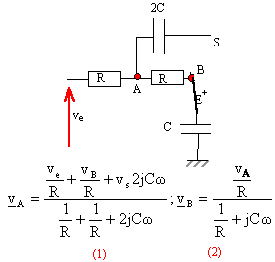( filtre de Butterworth) fonction de transfert : méthode de Millman de plus vB=vS ; (1) donne : vA[2/R+2jCw] =ve /R +vS [1/R+2jCw] vA[2+2jRCw] =ve +vS [1+2jRCw] (2) donne : vS [1+jRCw] = vA. vS [1+jRCw][2+2jRCw] =ve +vS [1+2jRCw] vS [1 +2jRCw-2(RCw)2]=ve ; H = vS / ve = [1 +2jRCw-2(RCw)2]-1. gain : c'est le module de H : H =[1 -2(RCw)2-2jRCw] / [1+4(RCw)4] G2(w) = {[1 -2(RCw)2]2+[2RCw]2}/[1+4(RCw)4] G(w) =[1+4(RCw)4]-½. déphasage du filtre : tan j = -2RCw/ [1 -2(RCw)2] et sin j = -2RCw/ [1+4(RCw)4]½. j appartient à l'intervalle [- p/2 ; 0] forme normalisée : H = [1 +2jRCw-(4RCw)2]-1= [1+2js w/w0-(w/ w0)²]-1. w20 = (2R²C²)-1 ; s2= ½ ; w20 = (2 *104*10-12)-1=108/2 ; w0 = 7071 rad/s. Le dénominateur de H est un polynôme du seconde degré : le filtre est d'ordre 2. gain en décibel : GdB= 20 log G(w) comportement asymptotique : w <10w0 : GdB= 20 log 1 = 0 ; w >10w0 : GdB= 20 log(w/ w0)-2= - 40 log(w/ w0) La bande passante du filtre passe-bas est la bande de fréquence comprise entre 0 et la fréquence de coupure à -3dB. -3= 20 log G(wC) ; G(wC) = 0,707 =[1+(wC/ w0)4]-½. 0,707 [1+(wC/ w0)4]½=1 ; 1+(wC/ w0)4 =2; (wC/ w0)4 = 1 soit wC= w0. fC= w0/ (2p) = 7071/6,28 = 1126 Hz.

analyse de Fourrier La tension d'entrée est une tension triangulaire de pulsation w0 et de période T0 = 2p/w0 ; la décomposition en série de Fourrier s'écrit : ve(t) = 8Em/p²[cos(w0t)+ 1/3² cos(3w0t)+ 1/5² cos(5w0t)+...] avec Em= 1 V. La tension de sortie us est une fonction sinusoïdale du temps. Définir fondamental et harmonique de rang n. Quelle est la pulsation w de la tension de sortie. Calculer l'amplitude de la tension de sortie.   corrigé Le fondamental est la composante ayant la même fréquence que le signal d'entrée de pulsation w0. La fréquence des harmoniques est proportionnelle à la fréquence du fondamental. L'harmonique de rang n a la pulsation n w0. Le signal de sortie est sinusoïdal et le filtre est un passe-bas, il ne reste que le fondamental w = w0. amplitude de sortie : ES max = G(w0) 8Em/p² = 0,707 *8/3,14² = 0,573 V.

étude du circuit en régime transitoire La tension d'entrée ve est quelconque. Déterminer l'équation différentielle du second ordre qui relie les deux tension ve et vs. La tension d'entrée est un échelon de tension, ve(t) = 0 si t<0 et ve(t) = E pour t>=0. E est une constante. La figure ci-dessous représente la tension de sortie vs en fonction du temps. Les valeurs numérique sont les mêmes que ci-dessus. 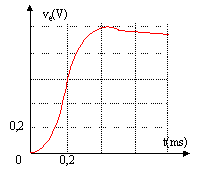- Quelle est la valeur de E ? - Quelle est la nature du régime transitoire observé ? Pourquoi ? Conclure. corrigé En régime sinusoïdal : [-(w/ w0)² + 2js w/w0 +1] vS = ve [(jw)²/ (w0)² + 2s (jw)/w0 +1] vS = ve à (jw)² correspond la dérivée seconde de vs(t) par rapport au temps. à (jw) correspond la dérivée première de vs(t) par rapport au temps. d'où l'équation différentielle : 1/ w0² d²vs/dt² + 2s / w0dvs/dt + vs(t) = ve(t) Au bout d'un temps très grand, la tension de sortie prend la valeur E=1V. Le régime est oscillatoire amorti. L'oscillation est très faible ( s légerement inférieur à 1). On atteint rapidement le régime permanent, pratiquement sans oscillation. retour - menu