champs électriques crée par diverses distributions de charges interaction de deux courants filiformes d'après Enac 99 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . .

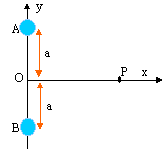
électrostatique Une sphère de rayon b porte une charge positive Q répartie uniformément sur sa surface. En s'aidant du théorème de Gauss, calculer le potentiel V crée par la charge Q à l'intérieur de la sphère. L'origine des potentiels est prise à l'infini. Deux sphères identiques du type précédent portent chacune la charge positive Q répartie uniformément sur leur surface. Leurs centres A et B distants de 2a ( a>b) sont disposées sur l'axe Oy symétriquement par rapport à l'origine O. Une troisième charge -2Q qui peur être considérée comme ponctuelle se trouve en O. Donner l'expression du vecteur champ électrostatique E(P) crée par les trois charges au point P de l'axe Ox d'abscisse x positive. 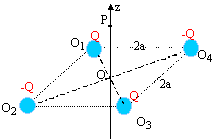Quatre sphères identiques du type précédent portant la même charge positive Q sont placées aux sommets O1, O2, O3, O4 d'un carré de côté 2a ( a>b). Donner l'expression du vecteur champ électrostatique E'(P) crée par les quatre charges au point P de l'axe Oz d'abscisse z. Deux sphères identiques du type précédent centrées en O1 et O2 portent la charge positive Q ; deux autres sphères analogues centrées en O2 et O4 portent la charge négative -Q. Donner l'expression du vecteur champ électrostatique E''(P) crée par les quatre charges au point P de l'axe Oz d'abscisse z. corrigé La distribution de charge a la symétrie sphérique : en conséquence le champ électrique E est radial et sa valeur au point P ne dépend que de la distance OP. A l'extérieur de la sphère le potentiel et le champ électrique se calculent comme si toute la charge Q était placée au centre de la sphère. le champ est nul à l'intérieur ( absence de charge) ; il n'est pas défini à la surface de la sphère ; il subit une discontiniuté à la traversée de cette surface chargée. par contre, le potentiel est défini en tout point, y compris à la surface de la sphère : étant nul à l'infini, sa valeur sur la surface de la sphère est : V= Q/(4pe0) b-1. point P extérieur aux sphères chargées: le champ électrique E est identique à celui crée par 3 charges ponctuelles. Par symétrique le champ électrique total E(P) en P est porté par l'axe Ox. 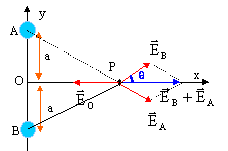OP=x ; AP=BP=(a²+x²)½ ; E0(P)= -2Q/(4pe0) x-2ux ; EA(P)+EB(P) = 2Q/(4pe0) (a²+x²) -2 cos q ux ; avec cos q = x / (a²+x²)½ ; EA(P)+EB(P) =2Q x /(4pe0) (a²+x²) -3/2 ux ; E(P)= 2Q /(4pe0)[x (a²+x²) -3/2 - x-2 ]ux ; par symétrie le champ E'(P) est dirigé suivant Oz. OO12 =2a2 ; O1P2 = OO12 + OP2 = 2a2 + z2 ; champ crée par une charge en P ( projection sur Oz) :E1(P)= Q/(4pe0)( 2a2 + z2)-2 cos q uz ; avec cos q = z / (2a²+z²)½ ; q angle formé entre OP et O1P E1(P)= Q z /(4pe0)( 2a2 + z2)-3/2 uz ; champ total en P : E'(P) = 4Q z /(4pe0)( 2a2 + z2)-3/2 uz ; Le champ E13(P) créé en P par les charges Q placées en O1 et en O3 est dirigé suivant Oz Le champ E24(P) créé en P par les charges Q placées en O2 et en O4 est dirigé en sens contraire de Oz. ces deux champs ont même valeur, sont colinéaires et de sens contraire : le champ total E"(P) est nul.

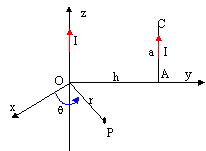
magnétostatique Un fil rectiligne de longueur infinie et de section négligeable est disposé suivant l'axe Oz du repère. Il est parcouru par un courant continu d'intensité I qui circule dans le sens de z positifs. Déterminer le vecteur champ magnétique B(P) crée au point P du plan (xOy) repéré par ses coordonnées polaires r et q. er et eq sont les vecteurs de la base polaire de P. Un second fil rectiligne de longueur a et de section négligeable est disposé dans le plan (xOy) selon le segment AC parallèle à Oz, à la distance h de cet axe. Il est parcouru par un courant continu d'intensité I. - Définir la résultante F des forces de Laplace qui s'exercent sur le fil AC. Déterminer le moment M(O) en O des forces de Laplace qui s'exercent sur le fil AC. Déterminer dans ces conditions la distance b qui sépare le point A du point K de AC, point où la force unique F peut être considérée comme appliquée à AC. 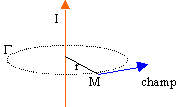corrigé le champ crée en M par le fil infini est orthoradial ; sa valeur ne dépend que de la distance OM. On applique le théorème d'Ampère sur un contour circulaire, d'axe Oz, passant par M. 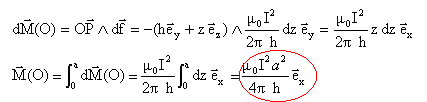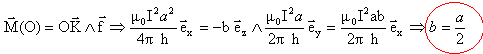Chaque élément de courant Idl du conducteur AC est soumis à la force de Laplace df : Le moment en O de la force élémentaire df est : Le point K est tel que : retour - menu