Problèmes à un degré de liberté deux ressorts verticaux pendule asymétrique oscillateur de Landau En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . .

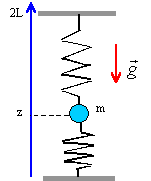
deux ressorts verticaux  les vecteurs sont écrits en gras et en bleu. Un solide de masse m est fixée à 2 ressorts verticaux de raideur k et de longueur à vide l0. Le mobile est astreint à des déplacements suivant la verticale. La position du centre de gravité du solide est repéré par la cote z. Dans un premier temps on néglige les frottements. Exprimer les énergies potentielles en fonction de z. Préciser les origines choisies. Etablir l'équation différentielle avec la variable z.. - A l'instant initial on läche le mobile à partir de la position z=½l0. Déterminer l'expression de z(t). - La période du mouvement est-elle modifiée si on part de 0,25 l0 ? Exprimer les forces s'exerçant sur le mobile en fonction de z ; retrouver la condition d'équilibre. - Etablir l'équation différentielle vérifiée par z. On tient compte des frottements en plaçant le dispositif dans un fluide visqueux de coefficient de viscosité h, qui exerce une force de freinage du type F= -6p h r v. Comment est modifiée l'équation différentielle ? La position d'équilibre est-elle changée ? La période des oscillations dans l'air est T0 et la pseudopériode dans un liquide est T. Etablir l'expression de la viscosité h du liquide en fonction de T0, T et des caractéristiques de la sphère. corrigé étude énergétique de l'oscillateur ( sans frottement) : énergie potentielle de pesanteur : (origine z=0) mgz énergie potentielle élastique, ressort inférieur : ½k(z-l0)2. ressort supérieur : ½k(2L-z-l0)2. énergie potentielle totale : Ep= mgz + ½k(z-l0)2+ ½k(2L-z-l0)2. Les positions d'équilibre corespondent aux extrémums de l'énergie potentielle : dériver Ep par rapport à z et rechercher les valeurs de z qui annullnt cette dérivée. dEp/dz = mg + k(z-l0) -k(2L-z-l0) = mg+2kz-2kL=0 d'où zéqui = L-mg/ (2k). absence de frottement, donc l'énergie mécanique se conserve : énergie cinétique = ½mv²; Eméca = Ep+Ecinétique. Eméca =mgz + ½k(z-l0)2+ ½k(2L-z-l0)2 + ½mv² dériver par rapport au temps : 0= mgz' +k(z-l0)z'-k(2L-z-l0)z' +mvv' or v'=z''; v=z' et en divisant chaque terme par v il vient : mg +2kz-2kL+mz"=0 z"+2k/m z = 2kL/m-g. (1) avec w02 = 2k/m solution de cette éauation différentielle : solution particulière de (1) : z(t) = L-gm/(2k) solution générale de z"+w02 z=0 : z(t) = A cos(w0t) solution générale de (1) : z(t) = A cos(w0t) + L-gm/(2k) Comment trouver A ? : à l'instant initial la position est z0 = ½L d'où : ½L = A+L-gm/(2k) ; A= - ½L+gm/(2k); z(t) = (- ½L+gm/(2k)] cos(w0t) + L-gm/(2k) l'équation différentielle (1) est homogène, la période T0 =2p/w0 est donc indépendante de la position initiale. Inventaire des forces : n ,vecteur unitaire de l'axe z. tension exercée par le ressort inférieur, verticale, vers le bas ( hypothèse : ce ressort n'est pas comprimé) : T1 = -k(z-l0)n tension exercée par le ressort du haut, verticale, vers le haut : T2 = k(2L-z-l0)n poids, verticale, vers le bas : P= - mg n A l'équilibre la somme des forces s'exerçant sur la sphère est nulle : -k(z équi -l0) + k(2L-z équi -l0) -mg=0 soit z équi = L-mg / (2k). La relation fondamentale de la dynamique donne : T1 +T2 +P= = ma. en projection sur l'axe z : -k(z-l0) + k(2L-z-l0) -mg = mz" mz" + 2kz = mg -2kL ou z" + 2k/m z = g-2kL/m On tien compte de la force de frottement :F= -6p h r v. T1 +T2 +P + F = ma. en projection sur l'axe z : -k(z-l0) + k(2L-z-l0) -mg -6p h r z' = mz" la position d'équilibre est obtenue en annulant lse deux termes en z' et z", d'où : -k(zéqui-l0) + k(2L-zéqui-l0) -mg =0 soit z équi = L-mg / (2k). Les frottements fluides ne modifient pas la position d'équilibre, contrairement aux frottements solides. équation différentielle : mz"+ 6p h r z' + 2kz = mg -2kL z"+ 6p h r/m z' + 2k/m z = g -2kL/m . On pose w02 = 2k/m et l =3p h r/m z" +2l z'+ w02 z = g -2kL/m. équation sans second membre : z" +2l z'+ w02 z =0 écquation caractéristique : x2 +2l x+ w02 =0 ; discriminant : D= 4l²-4w02 si D négatif, régime oscillatoire amorti de période T= 2p/w avec w ²= w02 -l2 soit 4p2/ T2 =4p2/ T02 - l2 l2 = 4p2(1/T02 -1/T2 ) ; l = 2p(1/T02 -1/T2 )½. Or l =3p h r/m d'où : h = 2m /(3r)(1/T02 -1/T2 )½.

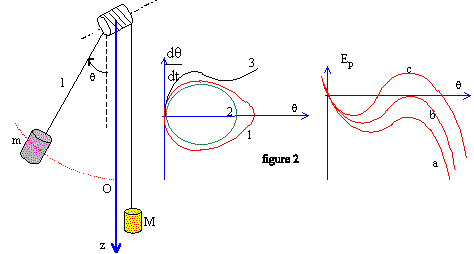
pendule asymétrique Un objet, de masse m est fixé sur une tige très légère, solidaire d'un cylindre de masse négligeable. Ce cylindre, de rayon R, peut tourner sans frottement autout d'un axe horizontal. Un fil de masse négligeable est enroulé sur le cylindre. Lorsque le cylindre tourne d'un angle q, la masse M se déplace verticalement vers le bas jusqu' à la cote z.. On admet que le système constitué par les deux masses m et M est conservatif. Le fil est inextensible, éccrire une relation entre R, q et z si les deux masses sont à la même altitude lorsque q =0. En déduire l'énergie cinétique Ec du système constitué par les deux masses en fonction de m, M, l et q '=dq/dt.. - Montrer que l'énergie potentielle Ep peut s'exprimer en fonction de la seule variable q. Si la masse M dépasse une certaine valeur M0, on constate qu'il n'existe plus de position d'équilibre. Exprimer M0 en fonction de m, l et R. Dans la suite M est inférieure à M0. Montrer qu'il existe deux positions d'équilibre qe1 et qe2 . - Discuter de la stabilité de ces positions d'équilibre. Au voisinage de ces positions d'équilibre on peut approximer l'énergie potentielle Ep(q) par Ep(q)= E0+C(q-qe)². Justifier cette approximation, expliciter la constante C et donner son signe pour chaque position d'équilibre. Etablir l'équation du mouvement en supposant que la position angulaire initiale est proche de qe1 puis de qe2. Justifier à nouveau le caractère stable ou instable de ces positions d'équilibre. Le système est placée dans la position q=0. Les masses sont lachées sans vitesse initiale à la date t=0. La figure 2 ci-dessus représente les trajectoires de phases pour l=50 cm, R= 5cm, m=100g et pour trois valeurs différentes de M, à savoir M=650g, 720g, 800 g. Associer à chaque valeur de M la trajectoire correspondante et préciser son sens de parcours. Justifier à partir du graphe Ep(q). - Comment choisir M pour obtenir des trajectoires fermées en partant de ces conditions initiales. corrigé les vecteurs sont écrits en gras et en bleu. Si l'angle q passe de zéro à une valeur positive, le cylindre tourne d'un angle q et le fil inextensible se déroule d'une longueur Rq ; alors la masse M descend de la valeur z = Rq avec q en radians. L'énergie cinétique de l'ensemble ( masse m et masse M) est la somme de l'énergie cinétique de chaque masse : ½MvM² = ½M(dz/dt)² =½MR2(dq/dt)2 ; ½mvm² = ½ml2(dq/dt)2. Ec = ½(MR2 +ml2)(dq/dt)2. énergie potentielle de pesanteur ( origine q =0 et z=0) -Mgz : la masse M descend quand la masse m s'élève + mg l ( 1-cosq) soit Ep = -MgRq + mg l ( 1-cosq). recherche des positions d'équilibre : dériver l'énergie potentielle par rapport à q puis chercher les valeurs de q qui annule cette dérivée. dEp/dq = -MgR + mg l sinq =0 soit -MgR + mg l sinq =0 sin q = MR/(ml) ; il y a une (des) solution(s) si MR/(ml) est inférieur ou égal à un. d'où la valeur maximale de M : M0=ml/R. Danas la mesure où M<M0 alors il y a deux solutions à l'équation sin q = MR/(ml) q e1 = sin-1(MR/(ml)=sin-1(M/M0) et q e2 = p-q e2 .( ces deux positions d'équilibre sont situées sur la même verticale) stabilité de l'équilibre : recherche du signe de la dérivée seconde d²Ep/dq ² = mglcosq. si q appartient à [0 ; ½p] alors cosq >0 et d²Ep/dq ² >0, équilibre stable correspondant à q e1 . si q appartient à [½p ; p] alors cosq <0 et d²Ep/dq ² <0, équilibre instable correspondant à q e2 développement limité au 2ème ordre de l'expression de l'énergie potentielle au voisinage d'une position d'équilibre : f (a+h) = f(a) + h(f '(a)+ ½h² f '' (a) avec a = qe et a+h =q d'où h = q -qe Ep(q)= Ep(qe) + (q -qe)f ' (qe) + ½(q -qe)² f " (qe) Or f ' (qe) =0 ( condition d'équilibre) et f " (qe) = d²Ep(qe)/dq ² = mglcosq. d'où Ep(q) voisin de : Ep(qe) + ½ d²Ep(qe)/dq ² (q -qe)² soit C= 2 d²Ep(qe)/dq ² C1 = 2 mgl cosqe1 = 2 mgl (1-sin² qe1)½=2mgl ((1-M²/M0²) ½ positif C2 = 2 mgl cosqe2 =2 mgl cos(p-qe1)= - 2 mgl cosqe1 ; négatif Expression de l'énergie mécanique au voisinage d'une position d'équilibre : E= Ec+ Ep = ½(MR2 +ml2)(dq/dt)2+ Ep(qe) + ½ d²Ep(qe)/dq ² (q -qe)² = constante ½(MR2 +ml2) q ' 2 + Ep(qe) + C (q -qe)² = constante dériver par rapport au temps : 0 = (MR2 +ml2) q ' q " +2C(q -qe) q ' donne q '=0 et q " + 2C/(MR2 +ml2) q = 2C/(MR2 +ml2) qe. pour q =qe1 : C=C1>0, on pose w0²= 2C1/(MR2 +ml2) d'où : q " + w0² q = w0² qe1. solution du type : q = qe1 + Acos (w0t + j) ; q reste dans l'intervalle [ qe + A ; qe - A] on reste autour de la position d'équilibre qe1 pour q =qe2 : C=C2<0, on pose w0²= - 2C2/(MR2 +ml2) d'où : q " - w0² q = -w0² qe2. solution du type : q = qe2 + Aexp(w0t) +B exp(-w0t) ; A et B ne peuvent s'annuler simultanément et en conséquence q - qe2 diverge au cours du temps comme exp(w0t). Equilibre instable. l'énergie potentielle initiale des deux masse est nulle ; l'énergie cinétique initiale est nulle ; donc l'énergie mécanique initiale est nulle. d'autre part, d'après la figure 2, l'énergie potentielle admet un maxima relatif pour q = qe2 : Deux cas sont alors possibles : Ep(qe2 ) >0 : l'énergie cinétique du système s'annule pour un angle q1 compris entre 0 et qe2 . Le système est confiné entre deux barrières de potentiel q =0 et q =q1. (courbe 1) Ep(qe2 ) <0 : l'énergie cinétique du système ne s'annule pas pour q = qe2 . L'angle dépasse la valeur qe2puis le système effectue ensuite des révolutions. (courbe 3) La valeur critique Mc de la masse M qui détermine le passage d'une trajectoire de phase fermée à une trajectoire ouverte est solution de l'équation Ep(qe2 ) =0 soit 0 = -MRqe2 + m l ( 1-cosqe2) avec sin qe2 = M/M0 et M0 = ml/R -Mqe2 + M0 ( 1-cosqe2) =0 ou bien : ( 1-cosqe2) = qe2 sin qe2 . sin²(½qe2)= qe2 sin (½qe2) cos(½qe2) tan (½qe2) = qe2 soit qe2= 2,331. Mc= M0 sin 2,331 = 0,724 kg.

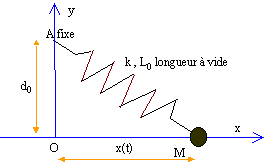
oscillateur de Landau   M est un solide de petites dimensions de masse m, accroché à un ressort ( masse négligeable) de raideur k, de longueur à vide L0. L'autre extrémité du ressort est fxe en A. M peut coulisser sans frottement sur la tige horizontale OM. Exprimer l'énergie potentielle élastique du système en prenannt Ep élastique = 0 en x =0. Rechercher des positions d'équilibre. - Distinguer différents cas suivant la valeur de d0. Donner alors l'allure de Ep élastique en fonction de x - Tracer sur un graphique en trait plein les positions d'équilibre stable en fonction de d0, et en trait pointillé les positions d'équilibre instable. Exprimer la pulsation propre des oscillations de faible amplitude autour des positions d'équilibre stable en fonction de d0, L0, k et m en supposant d0 différent de L0. Si d0 = L0 exprimer la période des petites oscillations . Cet oscillateur est-il harmonique ? corrigé Energie potentielle élastique du système : Ep, élastique = ½k(L-L0)2 avec L²= d0²+x² l'énergie potentielle de pesanteur de la masse est constante car elle se déplace sur un plan horizontal. positions d'équilibre : dériver l'énergie potentielle par rapport à la variable x et rechercher les valeurs de x qui annulent la dérivée. dEp, élastique /dx = k(L-L0)x / L =0 d'où x=0 et L=L0 soit d0²+x² = L0² soit x²= L0² -d0² ce qui impose L0>d0 ( sinon il n'y a qu'une seule solution x=0) stabilité de l'équilibre : x=0 et L0<d0 recherche du signe de la dérivée seconde : poser u= k(L-L0)x et v=L u'= kx²/L+k(L-L0) ; v'= x/L puis (u'v-v'u)/ v² d²Ep, élastique /dx² = kx²/L² + k(L-L0)/L -x²/L3 k(L-L0) pour x=0 , d²Ep, élastique /dx² =k(L-L0)/L =(d0-L0)/d0. positive, donc équilibre stable. second cas : L0>d0 ; x1=0 et x2= (L0² -d0² ) ½ et x2= -(L0² -d0² ) ½ . pour x =0 , la dérivée seconde est cette fois négative, équilibre instable. 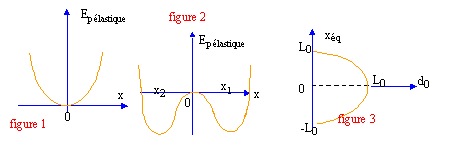pour x= (L0² -d0² ) ½ : d²Ep, élastique /dx² = k(L0² -d0² )/L² + k(L-L0)/L -(L0² -d0² )/L3 k(L-L0) = k(L0² -d0² )/d0² positive donc équilibre stable ( même chose pour x=x3) figure 3 : en trait plein les posirions stables d'équilibre ; en pointillés les positions instables pour L0=d0, le système bifurque vers d'autres positions d'équilibre que x=0. l'allure du tracé ( figure 2) rappelle une fourche d'où le nom " bifurcation fourche" Petites oscillations autour d'une position d'équilibre stable: le mouvement se fait suivant Ox : le système peut être modélisé par un oscillateur harmonique ( ressort fictif de raideur kmodèle ) de pulsation w = (kmodèle /m)½. kmodèle est égale à la valeur de la dérivée seconde de l'énergie potentielle totale par rapport à x pour x= xéq. d0>L0 kmodèle =k(d0-L0)/ d0. d0<L0 kmodèle =k(L²0-d²0)/ d²0. pour L0=d0, période des petites oscillations : la dérivée seconde de l'énergie potentielle étant nulle il faut la développer à un ordre supérieur. L'oscillateur n'est pas un oscillateur harmonique ; l'allure de la courbe représentant l'énergie potentielle ressemble à une parabole très aplatie. Ecrire la conservation de l'énergie mécanique : E= ½m x' ² + ½k(L-L0)2 = ½k((d0²+x0²)½-L0)2 avec L²= d0²+x² soit x' = dx/dt ={ k m-1[((d0²+x0²)½-L0)2 -((d0²+x²)½-L0)2]}½. pour les petites oscillations x0<<d0 et x<< d0 soit : (d0²+x0²)½ = d0 ( x0²/d0²+1)½ proche de : d0 ( ½x0²/d0²+1) et (d0²+x0²)½-L0)2 proche de : [d0 ( ½x0²/d0²+1) -d0 ]²= [d0 ½x0²/d0² ]². de même : (d0²+x²)½ proche de : d0 ( ½x²/d0²+1) et ((d0²+x²)½-L0)2 proche de : [d0 ½x²/d0² ]². par suite : x' = dx/dt proche { ½ k m-1d0-1[ x04 -x4]½}. dt = { k-1 2m d0[ x04 -x4]-½} dx changement de variable u = x/x0 : dt = { k-1 2m d0x0-2[ 1-u4]-½} du intégration entre 0 et x = x0 ( u=1) ; il s'écoule un quart de période T durant ce parcourt. 0,25 T = k-1 2m d0x0-1 retour - menu