|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
||
| .
. |
||
|
||
|
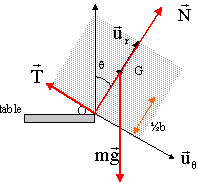
Un parallélépipède rectangle droit, homogène, noté S, de dimensions a, b, c, de centre d'inertie G ,de masse m est posé sur le bord d'une table. Dans cette position instable, il subit une action très faible qui provoque son basculement autour de O ,sans lui communiquer de vitesse initiale. Au début du mouvement il n'y a pas de glissement en O, l'action de la table est modélisée par une force R. L'axe parallèle au bord de la table passant par O est noté D. Le moment d'inertie du solide S par rapport à D est : J D = m /3 [a²/4 +b²]. Les grandeurs écrites en bleu et gras sont des vecteurs. 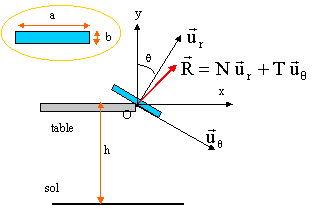
corrigé |
||
|
système étudié : le solide S ; référentiel galiléen lié à la table. Tant que le solide S ne glisse pas, la puissance de l'action de contact avec la table est nulle ; le système est conservatif et l'énergie mécanique de ce dernier est constante. énergie mécanique à la date t = 0, solide à plat sur la table ( q =0°) : la surface de la table est choisie comme origine de l'énergie potentielle de pesanteur ; l'altitude du centre de gravité du solide est ½ b et l'énergie mécanique vaut : EM = ½ m g b. à une date t ( rotation d'un angle q ): altitude de G :½ b sinq : énergie potentielle de pesanteur : ½ m g b cosq vitesse angulaire q' ; énergie cinétique : ½ JD q' ² énergie mécanique : EM =½ m g b cosq +½ JD q' ² conservation de l'énergie mécanique : ½ m g b =½ m g b cosq +½ JD q' ² q' ² = mg / JD b(1-cosq ). relation entre q et q " : q' = [mg / JD b(1-cosq )]½. dériver q' par rapport au temps : la dérivée de 1-cos q vaut : sin q q '. q" = ½[mg / JD b sin q q ' ] [mg / JD b(1-cosq )]-½ q" = ½mgb / JD sin q.
théorème de la résultante dynamique :
sur l'axe ur : N-mg cosq = - m ½b q' ² le signe moins vient du fait que l'accélération normale est dirigée vers O, en sens contraire de l'axe ur . avec q' ² = mg / JD b(1-cosq ). N = mg cosq - ½ m²b²g / JD (1-cosq ). sur l'axe uq : -T + mg sin q = m ½ b q" avec q" = ½mgb / JD sin q. T = mg sin q -m²gb² / (4JD )sin q = mg sin q[1 -mb² / (4JD )]. or JD = m /3 [a²/4 +b²] avec a = 10 b alors le terme mb² / (4JD ) est négligeable devant 1. T voisin de mg sin q et N voisin de mg cosq. T / (mg) voisin de sin q et N / (mg) voisin de cos q. glissement : le glissement apparaît quand la norme de T devient égale au coefficient de frottement f fois la norme de N T = f N soit f = T / N voisin de tan q voisin de 1. chute : Dès que le solide S commence à glisser, il perd contact avec la table et S est en chute libre. q'(q=p/4) =q'0 = [mg / JD b(1-cos(p/4 ))]½=[0,293 mbg / JD ]½ JD = 8,66 10-4 m ; q'0 = [0,293 *0,01*9,8 / 8,66 10-4]½ =5,75 rad/s plan de chute :
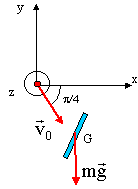
considérons l'axe Oz
perpendiculaire au plan de la figure la relation fondamentale de la dynamique s'écrit sue cet axe Oz : z" = 0 ; par intégration z' = Cte or la composante de la vitesse initiale est nulle sur Oz : par suite z' =0 et par intégration z = Cte. le mouvement s'effectue dans le plan Oxy. vitesse de rotation : dans le référentiel barycentrique lié au solide, le théorème du moment cinétique s'écrit : Le moment du poids est nul dans ce référentiel donc : J q" = 0 soit q' = Cte = q'0. équations horaires du mouvement de G :
v ( ½bq'0cos (p/4); -gt -½bq'0cos (p/4) ; 0) le vecteur position est une primitive du vecteur vitesse : OM ( x = ½bq'0cos (p/4)t +0,5 b cos (p/4) ; y = -½gt² -½bq'0cos (p/4) t + 0,5 b sin (p/4); 0) or ½bq'0cos (p/4) = 0,5 * 0,01 *5,75 *0,707 = 0,02 or 0,5 b sin (p/4) = 0,5*0,01*0,707 = 0,0035 durée de la chute : le second terme et le troisième terme dans l'expression de y sont rapidement négligeables devant ½gt² et la durée de la chute est voisine de : -h = -½gt² soit t² = 2h /g = 2*0,8 / 9,8 = 0,163 d'où t = 0,4s. de quel angle a tourné le solide ? : q = q0 + q'0t = p/4 + 5,75*0,4 = 3,08 rad.
retour - menu |