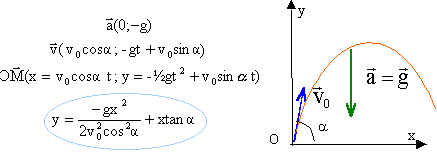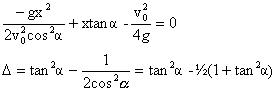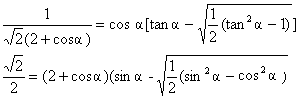Aurélie oct 2001
projectiles

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. 

. .
.
.

Un projectile de petites dimensions est lancé avec une vitesse inirtiale v0 faisant un angle a avec l'horizontale dans un champ de pesanteur uniforme. Les frottements sont négligeables.

  1. Donner l'expression de l'équation de la trajectoire du projectile.
  2. On recherche l'ensemble des points atteints par ce projectile dont :
    - la valeur de la vitesse initiale est constante.
    - l'inclinaison a varie
    Donner l'équation de cette parabole..
  3. Un second projectile se déplaçe suivant l'hotizontale, à l'altitude v0² / (4g) à la vitesse 2v0. Déterminer l'angle de tir a pour que le premier projectile atteigne le second en tir tendu.
corrigé
référentiel terrestre supposé galiléen

La trajectoire est une parabole d'axe Oy, contenue dans le plan Oxy, défini par la vitesse initiale et le vecteur accélération.

l'inconnue est dans ce cas l'angle a :

1/ cos² a =1+ tan²a : repport dans l'expression de la trajectoire.

y = -gx² / 2v0²(1+ tan²a) + x tan a.

tan²a + 2v0²/ (gx) tana +2v0² y / (gx²)-1 =0

il existe au moins une solution si le discriminant de cette équation du second degré est positif ou nul

D' = v04/ (g²x²) -2v0² y / (gx²)+1

l'équation d e la courbe cherchée est : v04/ (g²x²) -2v0² y / (gx²)+1=0

soit y = -g /(2v0²) x² + v0² / (2g)

parabole de sommet (0 : v0² / (2g))

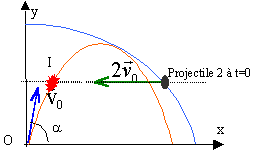
point de rencontre :

le second projectile est à t=0 au point d'ordonnée v0² / (4g).

Sa vitesse est horizontale de valeur 2v0 orientée en sens contraire de l'axe des abscisses

sa trajectoire est une droite horzontale d'ordonnée v0² / (4g).

son abscisse et son ordonnée vérifie l'équation : y = -g /(2v0²) x² + v0² / (2g)

d'où l'abscisse à t=0 :

v0² / (4g)= -g /(2v0²) x² + v0² / (2g)

conduit à x0= v0² / (1,414g)

l'abscisse en fonction du temps est : x2 = -2v0t + v0² / (1,414g)

Au point d'impact ( en supposant qu'il existe) :

D= ½( tan²a -1) positif si a >p/4.

le tir est tendu ; la solution cherchée est la plus petite racine de l'équation ci dessus.

le premier projectile se trouve en ce point I à la date : t = xI / (v0cosa)

le second projectile doit aussi s'y trouver : xI = -2v0 xI / (v0cosa) + v0² / (1,414g)

xI = -2 xI / cosa + v0² / (1,414g)

xI = v0²cosa / [1,414g(2+cosa)]

égaler ces deux dernières expressions de xI :

simplifier par v0²cosa /g.

résolution à la calculatrice a = 74°.

 

retour - menu