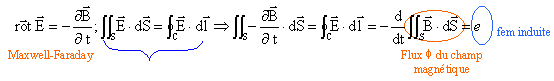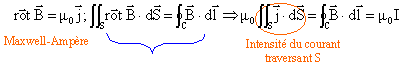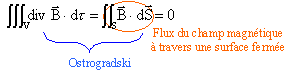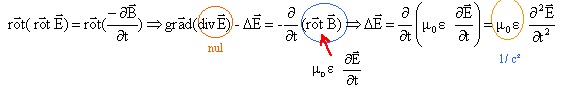|
rappels des lois fondamentales influence du champ magnétique terrestre En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|
| .
. |
|
|
|
|
Le problème a pour objet l'étude de la propagation des ondes hertziennes dans la haute atmosphère. L'action du champ de pesanteur sera partout négligé. Données : e = 1,6 10-19 C ; masse de l'électron me = 9 10-31 kg ; masse du proton mp = 1,67 10-27 kg ; c0= 3 108 m/s ; m0 = 4p 10-7 H/m ; rayon de la terre R= 6370 km ; champ magnétique terrestre au sol : B0 = 4,7 10-5 T rappels des lois fondamentales : les vecteurs sont écrits en gras et en bleu On donne les équations de Maxwell que doivent vérifier respectivement le vecteur champ électrique E et le vecteur champ magnétique B en notant r la densité volumique de charge et j le vecteur densité de courant. On souhaite en donner une interprétation physique
|
|
|
On applique le théorème d'Ostrogradski à l'équation de Maxwell-Gauss:
Le flux du champ électrostatique à travers une surface fermée est égal à Qint / e0.
loi de Faraday : On applique le théorème de Stockes à l'équation de Maxwell-Faraday : le contour C sera supposé fixe.
La loi de Faraday associée au phénomène d'induction électromagnétique
théorème d'Ampère : En régime permanent :
Expression du théorème d'Ampère il n'existe pas de charge magnétique : à partir de la relation de Maxwell concernant le flux du champ magnétique :
Le flux du champ magnétique à travers une surface fermée est nul du fait qu'il n'existe pas de charges magnétiques. En électrostatique, les lignes de champ sont issues des charges positives et aboutissent sur les charges négatives ; ces lignes sont des courbes ouvertes. Par contre du fait de l'absence de charges magnétiques les lignes de champ magnétique sont des courbes fermées. absence de charges électrique libres : la densité volumique de charges r =0 la densité de courant est nulle j = 0 remplacer e0 par e = e r e0 Les équations de Maxwell s'écrivent :
célérité de l'onde : Ecrire l'équation de Maxwell-Faraday puis prendre le rotationnel
la célérité c de l'onde est telle que c² m0 e0er =1 or c0² m0 e0 =1 d'où :c² er =c0². Le vecteur E1 correspond à une onde plane progressive dans le sens des x croissants. Le vecteur E2 correspond à une onde plane progressive dans le sens des x décroissants.
retour - menu |