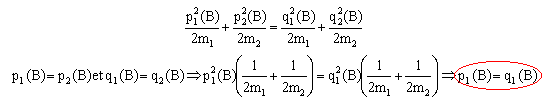Aurélie nov 2001
choc de deux particules

référentiel barycentrique (Mines d'Alès 91)

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.

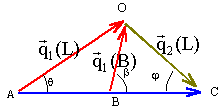
On considère le choc de deux particules supposées ponctuelles P1 de masse m1 et P2 de masse m2 pouvant se déplacer dans un plan. Soit Oxy un repère du laboratoire dans lequel la particule P2 se trouve initialement au repos en O.

On affecte de l'indice (L) les vitesses et quantités de mouvement mesurées dans le référentiel du laboratoire et de l'indice (B) les mêmes grandeurs mesurées dans le référentiel barycentrique.

Les lettres écrites en bleu et en gras correspondent à des vecteurs.

La particule P1 se déplace sur Ox et arrive sur P2 avec une vitesse initiale v1(L) et une quantité de mouvement p1(L). Après le choc on désigne par V1(L) et V2(L) les vitesses des particules P1 et P2 et par q1(L) et q2(L) leurs quantités de mouvement.

Le choc est considéré comme parfaitement élastique.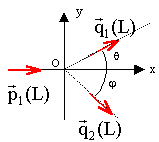

  1. Déterminer la vitesse VG(L) du barycentre G de P1 et de P2 en fonction de V1(L) , m1 et m2.
  2. Donner dans le référentiel barycentrique, les expressions des vitesses v1(B) et v2(B) de P1 et de P2 avant le choc en fonction de V1(L) , m1 et m2 puis de V1(B) et V2(B) de P1 et de P2 après le choc en fonction de V1(L) ,V2(L), m1 et m2.
  3. Montrer que dans le référentiel barycentrique, les particules P1 et P2 possèdent des quantités de mouvement p1(B) et p2(B) de même module avant le choc.
  4. Montrer que dans le référentiel barycentrique, les particules P1 et P2 possèdent des quantités de mouvement q1(B) et q2(B) de même module après le choc.
  1. Montrer que pour un choc parfaitement élastique p1(B) = q1(B) ( normes des vecteurs p1(B) = q1(B))
    Déterminer les expressions suivantes :
    - p1(L) en fonction de p1(B) , m1 et m2
    -     q1(L) en fonction de p1(B), q1(B), m1 et m2
    -     q2(L) en fonction de p1(B) et q1(B).
  2. Donner les expressions de AB en fonction de p1(B) , m1 et m2 et de BC en fonction de p1(B) : AC=p1(L).
    - Exprimer le module de q2(L) en fonction de p1(B) et de b.
    - Exprimer l'énergie cinétique Ec2 de P2 après le choc en fonction de p1(B), m2 et de b.
    - Exprimer l'énergie cinétique Ec1 de P1 après le choc en fonction de p1(B), m1 et m2.
  3. En traçant la hauteur OH, perpendiculaire en H au coté AC, montrer que tanq s'exprime uniquement en fonction de sinb, cosb et du rapport des masses.
Les lettres écrites en bleu et en gras correspondent à des vecteurs.

définition du barycentre : m1 GP1 + m2 GP2 = 0.

m1 (GO+OP1 )+ m2 (GO + OP2 ) = 0.

(m1 +m2 )(-OG)+ m1 OP1 + m2 OP2 = 0.

OG =(m1 OP1 + m2 OP2 ) / (m1 +m2 )

dérivation par rapport au temps pour faire apparaître les vitesses :

vG(L) = (m1 v1(L) + m2 v2(L) ) / (m1 +m2 )

avec v2(L)= 0 particule P2 immobile avant le choc.

vG(L) = m1 v1(L)/ (m1 +m2 )

lors du choc il y a conservation de la quantité de mouvement : vG(L) = Cte.

avant le choc :

GP1 =GO +OP1= -OG +OP1

dériver par rapport au temps pour faire apparaître les vitesses :

v1(B) = -vG(L) + v1(L)

remplacer vG(L) par son expression :

v1(B) = -m1 v1(L)/ (m1 +m2 ) +v1(L)= v1(L)[-m1/ (m1 +m2 )+1]

v1(B) = v1(L) m2/ (m1 +m2 )
de la même manière on trouve :

v2(B) = v1(L) (-m1) / (m1 +m2 )
après le choc :

V1(B) = -vG(L) + V1(L) avec : vG(L) = (m1 V1(L) + m2 V2(L) ) / (m1 +m2 )

V1(B) = - (m1 V1(L) + m2 V2(L) ) / (m1 +m2 ) + V1(L)

réduire au même dénominateur (m1 +m2 ), m1 V1(L) s'élimine :

V1(B) = m2/ (m1 +m2 ) [V1(L) -V2(L)]
part un calcul identique on trouve :

V2(B) = m1/ (m1 +m2 ) [V2(L) -V1(L)]

dans le référentiel barycentrique :

avant le choc

p1(B) = m1 v1(B) = m1 m2v1(L)/ (m1 +m2 )

p2(B) = m2 v2(B) = m2 (-m1)v1(L)/ (m1 +m2 )

p1(B) + p2(B) =0

p1(B) et p2(B) ont la même norme.

après le choc :

q1(B) = m1 V1(B) = m1 m2/ (m1 +m2 ) [V1(L) -V2(L)]

q2(B) = m2 V2(B) = m2 m1/ (m1 +m2 ) [V2(L) -V1(L)]

q1(B) + q2(B) =0

q1(B) et q2(B) ont la même norme.

choc élastique :

il y a conservation de l'énergie cinétique dans un choc élastique.

remarque : ½mv² = [mv]² / (2m)

soit dans le repère barycentrique :

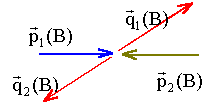
dans le référentiel barycentrique tous les vecteurs quantités de mouvement ont la même norme.

quantité de mouvement dans les deux repères :

avant le choc

p1(L) = m1 v1(L) = m1 [v1(B) +vG(L) ]

avec vG(L) = m1 v1(L)/ (m1 +m2 ) = p1(L)/ (m1 +m2 )

p1(L) = m1 v1(B) + p1(L) m1/(m1 +m2 )

p1(L) -p1(L) m2/(m1 +m2 ) = m1 v1(B) = p1(B)

réduction au même dénominateur p1(L) m1 disparaît

p1(L) m2/(m1 +m2 ) = p1(B)

p1(L) = p1(B) [1+m1/m2]
après le choc :

par un calcul analogue, à partir de :

q1(L) = m1 V1(L) = m1 [v1(B) +vG(L) ] on trouve :

q1(L) = q1(B) + m1/m2 p1(B)
par un calcul analogue, à partir de :

q2(L) = m2 V2(L) = m1 [v2(B) +vG(L) ] on trouve :

q2(L) = -q1(B) + p1(B)

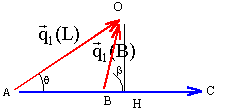
AB = AO + OB = AO - BO = q1(L)-q1(B)

avec q1(L) = q1(B) + m1/m2 p1(B)

d'où : AB =q1(B) + m1/m2 p1(B)-q1(B)

AB = m1/m2 p1(B)
BC = BA + AC = -AB +AC avec AC=p1(L)

BC = - m1/m2 p1(B)+q1(L)

avec p1(L) = p1(B) [1+m1/m2]

BC = p1(B)

OC = q2(L) = OB + BC= - q1(B) + p1(B)

utiliser la relation des triangles quelconques : a² = b² + c² - 2bc cos (b,c)

q2²(L) = q1²(B) + p1²(B) - 2 q1(B)p1(B)cos b.

or q1(B) = p1(B)

q2²(L) = 2p1²(B) (1- cos b) avec 2 sin²(½b) = (1- cos b)

q2(L) = 2p1(B)sin(½b)

énergie cinétique :

Ec2 = q2²(L) / (2m2) = 2p1²(B)sin²(½b) / m2.

Ec1 = p1²(L) / (2m1) avec p1(L) = p1(B) [1+m1/m2]

tan q :

dans le triangle AOH : tan q = OH / AH = OH / (AB+BH)

OH = q1(B) sinb ; AB = m1/m2 p1(B) ; BH = q1(B) cosb

tan q = sinb / [m1/m2 +cosb]

retour - menu