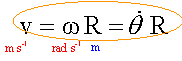|
travail, puissance, énergie En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
| .
. |
|
|
|
|
Un solide ponctuel M, de masse m; glisse sur un anneau de rayon R. Ce petit solide est fixé à l'extrémité d'un ressort de longueur à vide l0, de raideur k. L'autre extrémité du ressort est fixée en S. Les frottements sont négligés. 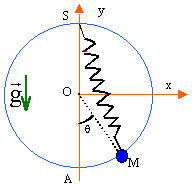
corrigé |
|
|
Expression de l'énergie cinétique : Ec = ½ m v²
Ec = ½ mR² q'². Expression de l'énergie potentielle de pesanteur : Epp = mg h l'origine de l'énergie potentielle de pesanteur est prise en O : h = -Rcos q. Epp = -mgRcos q. Expression de l'énergie potentielle élastique : Epé = ½ k (SM-l0)² l'origine de l'énergie potentielle élastique est telle que SMréf = l0 pour q = p/2
exprimer SM en fonction de R et q : dans le triangle quelconque OSM : SM² = OM² + OS² - 2 OM OS cos(p-q) avec OM=OS=R et cos (p-q) = - cos q SM² = R²+R² +2R² cosq = 2R² (1+ cosq) or (1+ cosq) = 2 cos ²(½q) SM² = 4 R² cos ²(½q) SM = 2R |cos(½q) | q appartient à [-p ; p ] donc q appartient à [-½p ; ½p ] soit |cos(½q) |= + cos(½q) SM = 2R cos(½q). Epé = ½ k (2R cos(½q)-l0)²
expression de l'énergie mécanique : ½ mR² q'² + ½ k (2R cos(½q)-l0)² - mgRcos q= cte Cette énergie
mécanique reste constante en l'absence de frottement.
Pour obtenir l'équation différentielle du mouvement de M, dériver l'expression de l'énergie par rapport au temps. dérivée de q'² : 2 q' q". dérivée de cos(½q) : -½ sin(½q) q' dérivée de u² : 2u u' dérivée de (2R cos(½q)-l0)² : 2 (2R cos(½q)-l0) (-2R½ sin(½q)q' ) dérivée de cos q : -sinq q' ½ mR² 2 q' q" + ½ k 2 (2R cos(½q)-l0) (-2R½ sin(½q) q' ) - mgR (-sinq) q' =0 R q' est commun à chaque terme et q' supposée non nulle : mR q" - k(2R cos(½q)-l0) sin(½q) + mgsinq = 0 avec 2 cos(½q)sin(½q) = sinq mR q" - kR sinq +kl0sin(½q)+ mgsinq = 0 q" + ( g/R-k/m)sinq + kl0 / (mR) sin(½q) =0. si q est petit : si l'amplitude est faible autour du point A alors sinq voisin de q radian et sin(½q ) voisin de ½q radian l'équation différentielle ci dessus s'écrit : q" + ( g/R-k/m)q + kl0 / (2mR) q =0. q" + (g/R-k/m + kl0 / (2mR) ) q =0. l'existence d'oscillation impose g/R-k/m + kl0 / (2mR) positif. g /R > k/m( l0 / (2R) -1)
retour - menu |