Mathématiques,
complexes, suites,
bac
S Nlle Calédonie 2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
|
Exercice 4. 3 points
Les questions 1. et 2. de cet exercice pourront être traitées de
manière indépendante.
On considère la suite des nombres complexes (z n) définie
pour tout entier naturel n par
z n =(1+i) / (1−i) n .
On se place dans le plan complexe d’origine O.
1. Pour tout entier
naturel n, on note A n le point d’affixe z n.
a. Démontrer que,
pour tout entier naturel n,
z n+4 / z n est réel.
Soit le nombre complexe 1+i ; son module est égal à 2 ½ et
son argument vaut p/4.
Soit le nombre
complexe 1-i ; son module est égal à 2½ et son argument vaut
-p/4.
Soit le nombre complexe (1-i)n ; son module
est égal à 2½n et son argument vaut -np/4.
Soit le nombre complexe zn ; son module est égal à 2½(1-n)
et son argument vaut (n+1)p/4.
Soit le nombre complexe
z n+4
; son module est égal à 2½(1-n-4) et son argument vaut
(n+4+1)p/4.
Soit le nombre complexe
z n+4 / z n ; son module est égal à 2½(1-2n-4)
et son argument vaut (n+4+1-n-1)p/4 soit.p.
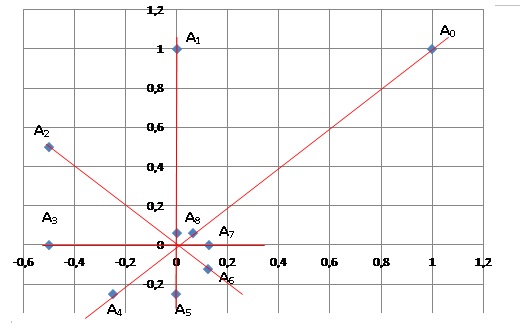
b. Démontrer alors
que, pour tout entier naturel n, les points O, A n et A n+4
sont alignés.
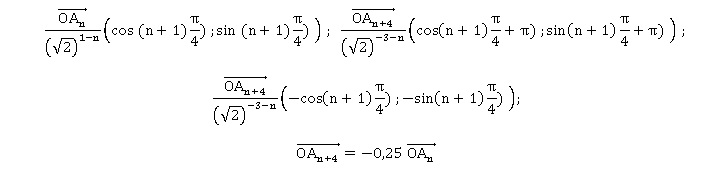 2.
2. Pour quelles
valeurs de n le nombre z n est-il réel ?
L'argument de z n doit être un multiple de p.
(n+1)p/4
= k p avec k
entier relatif.
n+1 = 4 k ; n = 4k-1.
|
|
| .
. |
|
|
|
Exercice 5. 5 points.
Soit (un) la suite définie par u0 = 3, u1
=6 et, pour tout entier naturel n :
un+2 =5 /4un+1−1 /4un.
Le but de cet exercice est d’étudier la limite éventuelle de la suite (un).
Partie A :
On souhaite calculer les valeurs des premiers termes de la suite (un)
à l’aide d’un tableur.
On a reproduit ci-dessous une partie d’une feuille de calcul, où
figurent les valeurs de u0 et de u1.
|
A
|
B
|
1
|
n
|
un
|
2
|
0
|
3
|
3
|
1
|
6
|
4
|
2
|
6,750
|
5
|
3
|
6,938
|
6
|
4
|
6,984
|
7
|
5
|
6,996
|
1. Donner une
formule qui, saisie dans la cellule B4, puis recopiée vers le bas,
permet d’obtenir des valeurs de la suite (un) dans la
colonne B.
=5/4*B3-0,25*B2
2. Recopier et
compléter le tableau ci-dessus. On donnera des valeurs approchées à 10−3
près de un pour n allant de 2 à 5.
3. Que peut-on
conjecturer à propos de la convergence de la suite (un) ?
On conjecture
que la suite (un) converge vers 7.
Partie B :
Étude de la suite
On considère les suites (vn) et (wn) définies
pour tout entier naturel n par :
vn =un+1 −0,25 un et wn
=un −7.
1. a. Démontrer que
(vn) est une suite constante.
Initialisation : v0
=u1 −0,25 u0 = 6-0,75 =5,25.
v1 =u2 −0,25 u1 =
6,75-1,5 =5,25.
La propriété est vraie au rang 1.
Hérédité :
vp = vp+1 est supposée vraie.
vp+2= up+3−0,25 up+2
= 1,25up+2−0,25up+1 −0,25
up+2
vp+2= up+2−0,25up+1 =vp+1.
La propriété est vraie au rang p+1.
Conclusion :
la propriété est vraie au rang 1 et héréditaire, donc elle est vraie
pour tout n.
.
|
|
|
|
b. En déduire que, pour tout entier naturel n, un+1
=0,25 un +21 / 4.
vn =un+1
−0,25 un = v0.
v0
=u1 −0,25 u0 =6-0,25x3=21 / 4.
Par
suite un+1 =0,25 un + 21 / 4.
2. a. En
utilisant le résultat de la question 1. b., montrer par récurrence que,
pour tout entier naturel n, un
<un+1 < 15.
Initialisation
: u0
<u1 < 15. La propriété est vraie au rang zéro.
Hérédité :
up <up+1 < 15 est
supposé vraie.
up+2= 0,25 up+1 +21 / 4.
up+2 < 0,25 x15 +21 /
4 ; up+2
<
0,25 x15 +21 / 4 ; up+2 < 9 soit up+2 <
15.
up+1= 0,25 up +21 /
4 ; up+1 < 0,25 x9 +21/4 ; up+1 < 30 / 4.
Par suite up+1 <up+2 < 15.
Conclusion
: la
propriété est vraie au rang 1 et héréditaire, donc elle est vraie pour
tout n.
b. En déduire que la suite (un)
est convergente.
un -un<un+1
-un< 15-un.
0 < un+1
-un< 15-un.
Or un est inférieur à 15, donc un+1 -un
>0.
La suite (un) est croissante et bornée par 15, donc elle
converge.
3. a. Démontrer que (wn) est une suite géométrique
dont on précisera le premier terme et
la raison.
wn
=un −7.
wn+1
=un+1 −7=0,25 un +21 / 4 -7 = 0,25 un -7 / 4
=0,25 (un-7) = 0,25 wn.
La suite est géométrique de raison q = 0,25.
w0 = u0-7 =3-7= -4.
b. En
déduire que, pour tout entier naturel n, un = 7−(1/4)n-1.
un =wn+7 ; wn = w0 x(1/4)n
= -4 x(1/4)n
; un =7 -4 x(1/4)n =7−(1/4)n-1.
c. Calculer la
limite de la suite (un).
-1 conséquent < 1/4 < 1 ; par (1/4)n-1 tend vers zéro quand n tend
vers l'infini.
La limite de la suite (un) est égale à 7.
|
|
|