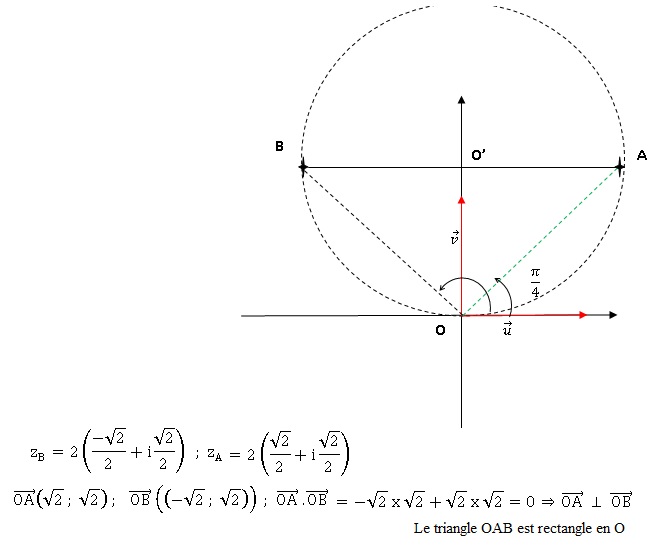
Mathématiques, nombres complexes, suite bac S Amérique du Sud 2017. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Exercice 4. 3 points Dans le plan complexe muni d’un repère orthonormé direct ; on considèreles points A et B d’affixes respectives zA = 2eiπ / 4 et zB = 2ei 3π / 4. 1. Montrer que OAB est un triangle rectangle isocèle. OA = 2 ; OB = 2. Le triangle OAB est isocèle en O. 2. On considère l’équation (E) : z2 −6½z +2 = 0. Montrer qu’une des solutions de (E) est l’affixe d’un point situé sur le cercle circonscrit au triangle OAB. Equation du cercle circonscrit au triangle OAB ( centre O' (0 ; 2½) et rayon R = O'A = 2½ cm). x2 +(y-2½)2 =2. Solutions de (E) : D = 6-4 x2 = -2 = 2 i2. . . 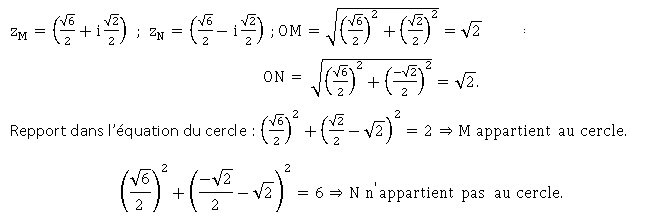Exercice 5. 5 points. Un biologiste souhaite étudier l’évolution de la population d’une espèce animale dans une réserve. Cette population est estimée à 12 000 individus en 2016. Les contraintes du milieu naturel font que la population ne peut pas dépasser les 60 000 individus. Partie A : un premier modèle. Dans une première approche, le biologiste estime que la population croît de 5% par an. L’évolution annuelle de la population est ainsi modélisée par une suite (vn) où vn représente le nombre d’individus, exprimé en milliers, en 2016+n. On a donc v0 = 12. 1. Déterminer la nature de la suite (vn) et donner l’expression de vn en fonction de n. On passe d'un terme au suivant en multipliant ce treme par 1,05. Il s'agit d'une suite géométrique de raison 1,05 et de premier terme 12. vn = 12 x 1,05n. 2. Ce modèle répond-il aux contraintes du milieu naturel ? -1 < 1,05 < 1, donc 1,05n tend vers l'infini quand n tend vers l'infini. La population dépassera les 60 000 individus en : 60 = 12 x1,05 n  n= ln (5) / ln(1,05) ~33 En 2016 +33 = 2049, la population dépasse 60 000 individus. Ce modèle ne convient pas. Partie B : un second modèle Le biologiste modélise ensuite l’évolution annuelle de la population par une suite (un) définie par u0 = 12 et, pour tout entier nature n, un+1 = −1,1 /605 u2n +1,1un . 1. On considère la fonction g définie sur R par g (x)= −1,1 /605 x2 +1,1x . a. Justifier que g est croissante sur [0; 60]. g'(x) = -2,2 / 605 x +1,1. g'(x) = 0 pour x =302,5. g'(x) est positive sur [0 ; 302,5[ et g(x) est donc strictement croissante sur cet intervalle. b. Résoudre dans R l’équation g (x) = x. −1,1 /605 x2 +1,1x = x. −1,1 /605 x2 +0,1x =0. x (0,1-1,1 / 605x) = 0. x =0 ; x =60,5 /1,1 = 55. 2. On remarquera que un+1 = g (un). a. Calculer la valeur arrondie à 10−3 de u1. Interpréter. u1 = g(u0)= g(12)= -1,1 / 605 x122+1,1 x12 ~12,938. En 2017, la population atteindra 12938 individus. b. Démontrer par récurrence que, pour tout entier naturel n, 0 < un  < 55. Initialisation : u0 =12. La propriété est vraie au rang zéro. Hérédité : on supose la propriété vraie au rang p :  0 < up  < 55. Par conséquence g(0) < g(un) < g(55), car g est croissante sur [0 ; 60 ]. 0 <  g(un)   < −1,1 /605 x552 +55 x1,1. 0 <  g(un)   < −1,1 /605 x552 +55 x1,1. 0 <  g(un)   < −5,5 +60,5. 0 <  g(un)   < 55. Conclusion : la propriété est vraie au rang zéro et héréditaire, elle est vraie pour tout entier n. c. Démontrer que la suite (un) est croissante. un+1-un= g(un)-un. un+1-un=−1,1 /605 u2n +0,1un. un+1-un=un(−1,1 /605 un +0,1). D'une part, un étant compris entre 0 et 55 est positif. D'autre part,  0 < un < 55 soit 0 > -1,1 / 605 un > -1,1 /605 x55 0 > -1,1 / 605 un > -0,1 0 +1,1> -1,1 / 605 un +1,1 > -0,1+1,1 1,1 > -1,1 / 605 un +1,1 > 1, donc -1,1 / 605 un +1,1 est positif. Par suite un+1-un est positif ; un+1 > un  ; la suite (un) est croissante. d. En déduire la convergence de la suite (un). La suite (un) est croissante et majorée par 55. Elle converge donc vers l < 55. e. On admet que la limite ℓ de la suite (un) vérifie g (ℓ) = ℓ. En déduire sa valeur et l’interpréter dans le contexte de l’exercice. g(l)=l ; la suite étant croissante et son premier terme étant égal à 12, l = 55. 3. Le biologiste souhaite déterminer le nombre d’années au bout duquel la population dépassera les 50 000 individus avec ce second modèle. Il utilise l’algorithme suivant. Variables : n entier naturel u réel Traitement : n prend la valeur 0 u prend la valeur 12 Tant que  u < 50 u prend la valeur −1,1 /605 u2+1,1u n prend la valeur n+1 Fin Tant que. Sortie : Afficher n Recopier et compléter cet algorithme afin qu’il affiche en sortie le plus petit entier r tel que ur >50.  .

menu