Mathématiques, fonction, géométrie dans l'espace, probabilités bac S Amérique du Sud 2017.

Exercice 1. 5 points
La chocolaterie Delmas décide de commercialiser de nouvelles confiseries : des palets au chocolat en forme de goutte d’eau.
Pour cela, elle doit fabriquer des moules sur mesure qui doivent répondre à la contrainte suivante : pour que cette gamme de bonbons soit rentable, la chocolaterie doit pouvoir en fabriquer au moins 80 avec 1 litre de pâte liquide au chocolat.
Partie A : modélisation par une jonction
Le demi contour de la face supérieure du palet sera modélisé par une portion de la courbe de la fonction f définie sur ]0 ; +∞[ par :
f (x) =(x² −2x −2−3ln x) / x.
La représentation graphique de la fonction f est donnée ci-dessous.

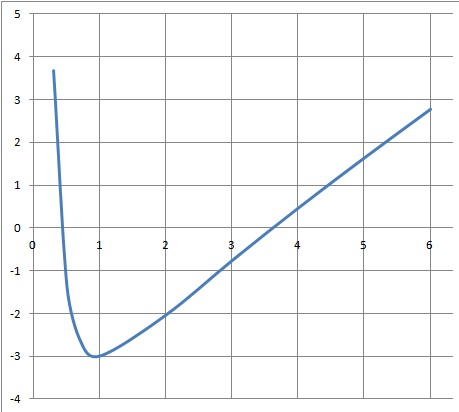
Le repère est orthogonal d’unité 2 cm en abscisses et 1 cm en ordonnées.
1. Soit ϕ la fonction définie sur ]0 ; +∞[ par :
ϕ(x) = x² −1+3lnx.
a. Calculer ϕ(1) et la limite de ϕ en 0.
F(1) = 1²-1+3ln(1) = 0.
Quand x tend vers zéro :
x²-1 tend vers -1 et ln(x) tend vers moins l'infini. F(x) tend donc vers moins l'infini.
b. Étudier les variations de ϕ sur ]0 ; +∞[.
En déduire le signe de ϕ(x) selon les valeurs de x.
La dérivée 2x +3 / x est positive sur ]0 ; +∞[.
F(x) est strictement croissante sur ]0 ; +∞[.
F(x) est négative sur ]0 ; 1[, nulle pour x=1 et positive sur ]1 ; +oo[.

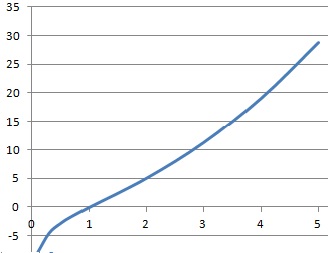
2. a. Calculer les limites de f aux bornes de son ensemble de définition.
f (x) =x −2 −(2+3ln (x)) / x.
Quand x tend vers zéro : x-2 tend vers -2 ; (2+3ln (x)) / x tend vers moins l'infini et -(2+3ln (x)) / x tend vers plus l'infini.
Par suite f(x) tend vers plus l'infini.
Quand x tend vers plus l'infini : x-2 tend vers plus l'infini ; (2+3ln (x)) / x tend vers zéro.
Par suite f(x) tend vers plus l'infini.
b. Montrer que sur ]0 ; +∞[ : f ′(x) = ϕ(x) / x² .
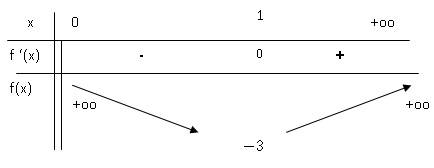
En déduire le tableau de variation de f .
On pose u =x² −2x −2−3ln x et v = x.
u' = 2x-2-3 / x = (2x²-2x-3) / x et v' = 1.
Dérivée d'un quotient : (u'v -v'u) / v² =[ (2x²-2x-3)-(x² −2x −2−3ln x) ] / x²=(x²-1+3ln x) / x²=F(x) / x².

c. Prouver que l’équation f (x) = 0 admet une unique solution α sur ]0; 1].
Déterminer à la calculatrice une valeur approchée de α à 10⁻² près.
Sur ]0 ; 1], f(x) est strictement décroissante.
De plus f(1) est négatif et f(0,1) est positif.
D'après le corolaire du théorème des valeurs intermédiaires, f(x) = 0 admet une unique solution sur ]0 ; 1].
Solution de f(x)=0, x ~ 0,41.
On admettra que l’équation f (x) = 0 a également une unique solution β sur [1 ; +∞[ avec β ≈ 3,61 à 10⁻² près.
d. Soit F la fonction définie sur ]0 ; +∞[ par :
F(x) =0,5 x² -2x -2ln(x) -1,5( ln(x))².
Montrer que F est une primitive de f sur ]0 ; +∞[.
Dériver F : F ' = 0,5 *2 x-2-2 / x-1,5*2 ln(x) / x = x-2-2 / x -3ln(x) / x = (x²-2x-2-3ln(x) ) / x = f(x).

Partie B : résolution du problème.
Dans cette partie, les calculs seront effectués avec les valeurs approchées à 10⁻² près de α et β de la partie A.
Pour obtenir la forme de la goutte, on considère la courbe représentative C de la fonction f restreinte à l’intervalle [α ; β] ainsi que son symétrique C′ par rapport à l’axe des abscisses. Les deux courbes C et C′ délimitent la face supérieure du palet. Pour des raisons
esthétiques, le chocolatier aimerait que ses palets aient une épaisseur de 0,5 cm.
Dans ces conditions, la contrainte de rentabilité serait-elle respectée ?
Aire du palet : 2 | F(ß)-F(a) |.
F(3,61) ~0,5*3,61²-2*3,61-2 ln(3,61)-1,5*(ln(3,61))² ~2 (5,743-0,142) ~11,2 unités d'aire soit 11,2 x2 =22,4 cm².
Volume du palet : 22,4 x0,5 = 11,2 cm³.
Volume de 80 palets : 896 cm³ = 0,896 L. La contrainte de rentabilité est respectée.