Mathématiques,  bac S Antilles 09 /2017 . En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Exercice 1. 7 points. Romane utilise deux modes de déplacement pour se déplacer entre son domicile et son lieu de travail : le vélo ou les transports en commun. Partie A. Lorsque la journée est ensoleillée, Romane se déplace en vélo 9 fois sur 10. Lorsque la journée n’est pas ensoleillée, Romane se déplace en vélo 6 fois sur 10. La probabilité qu’une journée soit ensoleillée, dans la ville où habite Romane, est notée p. Pour une journée donnée, on note : • E l’évènement « La journée est ensoleillée » ; • V l’évènement« Romane se déplace en vélo ». 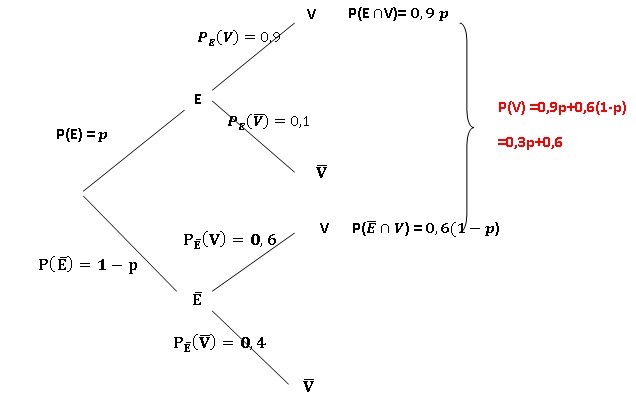1. Construire l’arbre pondéré représentant la situation. 2. Montrer que la probabilité que Romane se déplace en vélo lors d’une journée donnée est P(V ) = 0,3p +0,6. 3. On constate que dans 67,5% des cas, c’est en vélo que Romane se déplace entre son domicile et son lieu de travail. a. Calculer la valeur de p. 0,675=0,3p+0,6 ; 0,3p = 0,075 ; p = 0,25. b. Sachant que Romane s’est déplacée en vélo, montrer que la probabilité que la journée soit ensoleillée est 1/ 3. PV(E)=P(V n E) / P(V) = 0,9 p / 0,675 = 0,9 x0,25 / 0,675 = 1 /3. Partie B. Lorsque Romane se déplace en vélo, on modélise son temps de trajet, exprimé en minutes, entre son domicile et son lieu de travail par une variable aléatoire TV suivant une loi normale d’espérance μV et d’écart-type 1 minute. Lorsqu’elle effectue ce trajet en transports en commun, on modélise son temps de trajet, exprimé en minutes, par une variable aléatoire TC suivant une loi normale d’espérance μC et d’écart-type 3 minutes. 1. On nomme CC et CV les courbes représentatives des fonctions de densité des variables aléatoires TV et TC représentées dans la figure ci-dessous. Déterminer, en justifiant votre réponse, μV et μC . Les courbes sont symétriques par rapport aux droites d'équation t = 14 et t = 16. µV = 14 ; µC=16. L'écart type est un paramètre de dispersion autour de l'espérance. Plus l'écart type est petit, plus la courbe est étroite. 2. Calculer la probabilité que pour Romane un trajet domicile-travail en vélo dure entre 10 et 15 minutes. Arrondir la réponse à 10−4. P(10 < TV < 15)=P(15 < TV )-P(10 < TV ) =0,841345-3,16 10-5 =0,8413. 3. Quel mode de déplacement Romane doit-elle privilégier si elle souhaite mettre moins de 15minutes pour se rendre au travail ? P(15 < TV ) =0,8413 ; P(15 < TC )=0,3694. Le vélo est privilégié. Partie C. En hiver, Romane roule en vélo de nuit. Son vélo est visible grâce à une ampoule dont la durée de fonctionnement en heures peut être modélisée par une variable aléatoire, notée X, suivant une loi exponentielle de paramètre λ, réel strictement positif. La fonction de densité associée est donc la fonction f définie sur [0 ; +∞[ par f (t ) = λe−λt . 1. Soit b un réel positif. Démontrer, à l’aide d’une intégrale, que P(X < b) = 1−eλb. 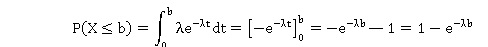2. On sait que la probabilité que l’ampoule fonctionne encore après 50 heures d’utilisation est 0,9. a. En déduire la valeur exacte de λ. P(X >50)=exp(-50 l)=0,9 ; exp(-50 l) =0,9 ; -50 l = ln(0,9) ; l = -ln(0,9) / 50. b. Calculer la probabilité que la durée de fonctionnement de l’ampoule soit supérieure à 250 heures sachant que l’ampoule a déjà fonctionné 200 heures. La loi exponentielle est sans mémoire. PX>200(X >250)=P( X < 250-200) =P(X >50) =0,9. . . .... ..... Exercice 2. 3 points. Soit la suite de nombres complexes (zn) définie par z0 = 100 zn+1 = i /3 zn  pour tout entier naturel n. Le plan est muni d’un repère orthonormé direct Pour tout entier naturel n, on note Mn le point d’affixe zn. 1. Démontrer que, pour tout entier naturel n, les points O, Mn et Mn+2 sont alignés. zn+2 =  i /3 zn+1 = i / 3 ( i / 3 zn )= i2 / 9 zn = -zn / 9. 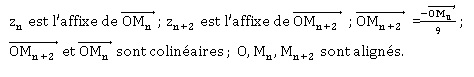2. On rappelle qu’un disque de centre A et de rayon r , où r est un nombre réel positif, est l’ensemble des points M du plan tels que AM < r . Démontrer que, à partir d’un certain rang, tous les points Mn appartiennent au disque de centre O et de rayon 1. OMn = |zn|. Les points M appartiennent au disque de centre O et de rayon r < 1 si |zn| < 1. zn+1= i / 3 zn ; |zn+1|=|zn| / 3 avec z0 = 100. La suite ( |zn|) est géométrique de premier terme 100 et de raison q = 1 / 3. -1 < q <1 : la suite est convergente et sa limite est nulle. |zn| = 100 x(1 /3) n ;  100 x(1 /3) n < 1. n ln(1 / 3 ) < ln (1 / 100) ; n >ln(100) / ln(3) ; n >5. Exercice 3. ( 5 points ). Partie A. Soit la fonction f définie et dérivable sur [1 ; +∞[ telle que, pour tout nombre réel x supérieur ou égal à 1, f (x) =1 / x ln(x). On note C la courbe représentative de f dans un repère orthonormé. 1. Démontrer que la courbe C admet une asymptote horizontale. Quand x tend vers l'infini, la limite de ln(x) / x est égale à zéro ; la droite d'équation y = 0 est asymptote à la courbe C. 2. Déterminer la fonction dérivée f ′ de la fonction f sur [1 ; +∞[. On pose u = ln(x) et v = x ; u' = 1/x et v' = 1. f '(x) = (u'v-v'u) / v2 = (1-ln(x)) / x2. 3. Étudier les variations de la fonction f sur [1 ; +∞[. Le signe de f '(x) est celui de 1-ln(x). 1-ln(x) est nul pour x =e. 1-ln(x) est négatif sur ]e ; +oo[ ; f(x) est strictement décroissante sur ]e ; +oo[. 1-ln(x) est positif sur [ 1 ; e[ ; f(x) est strictement croissante sur [ 1 ; e[. f(x) présente un maximum pour x = e avec  f(e) = 1 / e. Partie B. On considère la suite (un) définie pour tout en tier naturel par : 1. Démontrer que u0 =(ln2)2 / 2. Interpréter graphiquement ce résultat. 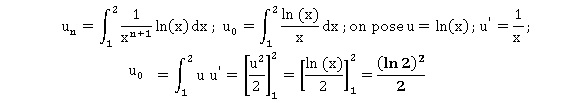La fonction f étant positive sur [1 ; 2), u0 représente l'aire ( en unité d'aire) du domaine compris entre la courbe C, l'axe des abscisses et les droitres d'équation x=1 et x = 2. 2. Prouver que, pour tout entier naturel n et pour tout nombre réel x de l’intervalle [1; 2], on a la relation suivante. 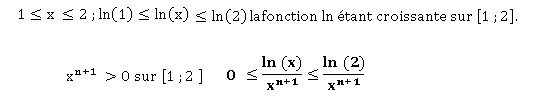3. 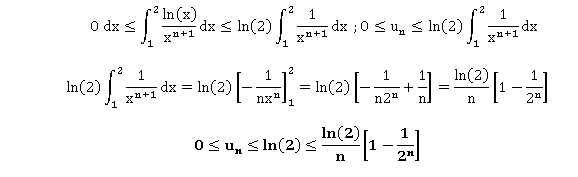En déduire que, pour tout entier naturel  n, on ala relation suivante : 4. Déterminer la limite de la suite (un). Quand n tend vers l'infini :  ln(2) / n tend vers zéro ; 1 /2n tend vers zéro ; 1-1/2n tend vers 1. ln(2) / n (1-1/2n ) tend vers zéro. D'après le théorème des gendarmes la suite (un) converge et tend vers zéro. Exercice 4. 5 points. On note R l’ensemble des nombres réels. L’espace est rapporté à un repère orthonormé On considère les points A(1; 1; 14), B(0 ; 1 ; 8) et C(−2 ; 2 ; 4) ainsi que le vecteur n de coordonnées : (6 ; 8 -1). 1. a. Justifier que les points A, B et C définissent un plan. b. Démontrer que le vecteur  n est orthogonal aux vecteurs AB et AC. c. Démontrer que le plan (ABC) a pour équation cartésienne 6x+8y−z = 0. L'équation du plan (ABC) est de la forme 6x+8y-z+d=0. A appartient à ce plan : 6*1 +8*1-14+d = 0 soit d = 0. 2. On considère la droite D des points M dont les coordonnées (x ; y ; z) sont données par : x = 2t-3 ; y = t-0,5 ; z = 4t+2 avec t réel. a. Donner un vecteur directeur de la droite D. Le vecteur de coordonnées (2 ; 1 ; 4) est un vecteur directeur de cette droite. b. La droite D et le plan (ABC) sont-ils sécants ? 6(2t-3)+8(t-0,5-(4t+2)=0. 12t-18+8t-4-4t-2=0 ; 16t =24 ; t = 1,5. La solution du système constitué par l'équation du plan et la représentation paramétrique de la droite, étant unique, la droite D et le plan (ABC) sont sécants au point de coordonnées ( 0 ; 1 ; 8). 3. Dans cette question, on considère l’ensemble (E) des points M dont les coordonnées (x ; y ; z) sont données par x = t 3 +t ; y = t +1 ; z = 2t avec t réel. Démontrer qu’il existe un unique point M qui appartient à la fois à (E) et à (ABC). Il n’est pas demandé de déterminer ses coordonnées. L'équation 6( t 3 +t) +8(t+1)-2t=0 doit avoir une solution réelle unique. 6t3+6t+8t+8-2t=0. 6t3+12t+8=0. t3+2t+4/3=0. On pose f(x) = x3+2x+4/3=0 définie sur R. f '(x) = 3x2+2. La dérivée étant positive sur R, f(x) est sttrictement croissante sur R. Quand x tend vers moins l'infini, la fonction tens vers moins l'infini. Quand x tend vers plus l'infini, la fonction tens vers plus l'infini. D'après le théorème des valeurs intermédiaire, f(x)=0 a une solution unique sur R. .

menu