Mathématiques, fonction, suite, géométrie, nombres complexes, bac S Métropole 2017 . En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Exercice 1. Partie A. On considère la fonction h définie sur l’intervalle 0;+∞ par :h(x)= x e-x. 1. Déterminer la limite de la fonction h en +∞. Par croissance comparée, la limite de ex /x, quand x tend vers l'infini, est égale plus l'infini. Donc la limite de 1 / (ex /x), quand x tend vers l'infini, est égale à zéro. Or h(x) = x / ex = 1 /(ex/x); par suite la limite de h(x) en plus l'infini est égale à zéro. 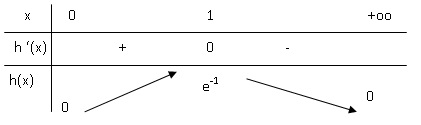2. Étudier les variations de la fonction h sur l’intervalle 0;+∞ et dresser son tableau de variations. Calculer la dérivée h' en posant u = x et v = e-x; u' = 1 ; v' = -e-x. h'(x) = u'v +v'u = e-x -xe-x=e-x(1-x). e-x est toujours positif. Le signe de h'(x) est celui de (1-x). Si x appartient à [0 ; 1], h'(x) est strictement positive et h(x) est strictement croissante. Si x appartient à ]1 ; +oo [, h'(x) est strictement négative et h(x) est strictement décroissante. Si x =1, h'(x) est nulle est h(x) présente un maximum h(1) = 1/e. 3. L’objectif de cette question est de déterminer une primitive de la fonction h. a. Vérifier que pour tout nombre réel x appartenant à l’intervalle 0;+∞ , on a : h(x) =e-x -h'(x). h(x) = xe-x ; h'(x) = e-x -xe-x ; ajouter : h(x) + h'(x) = e-x soit h(x) = e-x-h'(x). b. Déterminer une primitive sur l’intervalle 0;+∞ de la fonction e-x. -e-x. c. Déduire des deux questions précédentes une primitive de la fonction h sur l’intervalle 0;+∞ . H(x) = -e-x -h(x) = -e-x - xe-x =- e-x(x+1). Partie B On définit les fonctions f et  g sur l’intervalle 0;+∞ par : f(x) = xe-x+ln(x +1) ; g(x) = ln(x+1). On note Cf et Cg les représentations graphiques respectives des fonctions f et g dans un repère orthonormé. 1. Pour un nombre réel x appartenant à l’intervalle 0;+∞ , on appelle M le point de coordonnées (x ; f(x)) et N le point de coordonnées (x ; g(x)). M et N sont donc les points d’abscisse x appartenant respectivement aux courbes Cf et Cg. a. Déterminer la valeur de x pour laquelle la distance MN est maximale et donner cette distance maximale. MN =| g(x) - f(x) |= |ln(x+1) - xe-x-ln(x +1)| = |-xe-x|. xe-x étant positif, MN = x e-x. MN = h(x) ; MN est maximal pour x = 1 et vaut MNmax = e-1. 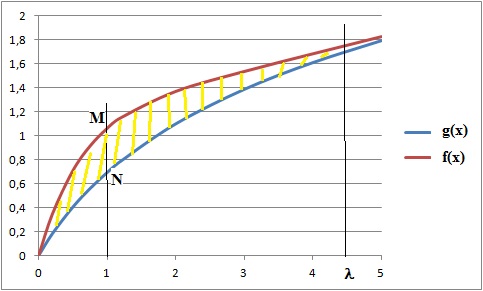b. Placer sur le graphique les points M et N correspondant à la valeur maximale de MN. . . .... ..... 2. Soit l un réel appartenant à l’intervalle 0;+∞ . On note Dl le domaine du plan délimité par les courbes Cf et Cg et par les droites d’équations x= 0 et x=l. a. Hachurer le domaine Dl correspondant à la valeur l proposée sur le graphique. b. On note Al l’aire du domaine Dl, exprimée en unités d’aire. Démontrer que : Al = 1-(l+1) / el. f(x) -g(x) = xe- : . Primitive de x e-x  : H(x) = - e-x(x+1). Al = [ - e-x(x+1)]0l = -e-l(1+l)+1 c. Calculer la limite de Al lorsque l tend vers +∞ et interpréter le résultat. Par croissance comparée (l+1) / el tend vers zéro quand l tend vers l'infini. En conséquence Al tend vers 1. L'aire du domaine compris entre les deux courbes est égale à 1. 3. On considère l’algorithme suivant : Variables : l est un réel positif S est un réel strictement compris entre 0 et 1. Initialisation : Saisir S l prend la valeur 0 Traitement : Tant Que 1 -(l+1)e-l < S faire l prend la valeur l+ 1 Fin Tant Que Sortie : Afficher l a. Quelle valeur affiche cet algorithme si on saisit la valeur S=0,8 ? A0 = 0 ; A1 = 0,264 ; A2 = 0,594 ; A3 = 0,8009. Cet algorithme affiche 3. b. Quel est le rôle de cet algorithme ? Cet algorithme donne le plus petit entier l pour lequel Al > S Exercice 2. L’espace est muni d’un repère orthonormé (O, i, j, k). Soit P le plan d’équation cartésienne : 2x −z − 3 = 0. On note A le point de coordonnées (1 ; a ; a2), où a est un nombre réel. 1. Justifier que, quelle que soit la valeur du réel a, le point A n’appartient pas au plan P. Si A appartient au plan P, ces coordonnées vérifient l'équation cartésienne de ce plan. 2-a2-3 =0 ; a2 = -1 ; impossible.  A n'appartient pas au plan P. 2. a. Déterminer une représentation paramétrique de la droite D (de paramètre noté t) passant par le point A et orthogonale au plan P. Coordonnées d'un vecteur directeur de cette droite : (2 ; 0 ; -1). Représentation paramétrique de cette droite ; x = 2t +xA =2t +1. y = 0 +yA = a ; z = -t +zA = -t +a2. b. Soit M un point appartenant à la droite D, associé à la valeur t du paramètre dans la représentation paramétrique précédente. Exprimer la distance AM en fonction du réel . AM2 = (2t+1-1)2 +(a -a)2 +(-t+a2-a2)2. AM2 =4t2+t2=5t2. AM= 5½|t|. On note H le point d’intersection du plan P et de la droite D orthogonale à P et passant par le point A. Le point H est appelé le projeté orthogonal du point A sur le plan P, et la distance AH est appelée distance du point A au plan P. 3. Existe-t-il une valeur de a pour laquelle la distance AH du point A de coordonnées (1 ;a ; a2) au plan P est minimale ? Justifier la réponse. H appartient à la fois au plan P et à la droite D. Les coordonnées de H vérifient : xH = 2t+1 ; yH = a ; zH = -t+a2. 2xH-zH-3 = 0 ; 4t+2+t-a2-3=0 ; 5t =a2 +1 ; t =(a2+1) /5. D'après la question précédente AH = 5½|t| soit. AH= |a2+1| /5½ =(a2+1) /5½ . AH est minimum si a = 0 ; AHmini = 5-½. Exercice 3. Dans une vaste plaine, un réseau de capteurs permet de détecter la foudre et de produire une image des phénomènes orageux. Ces données servent en particulier aux services météorologiques pour améliorer leurs prévisions et pour permettre des interventions plus rapides sur les lieux, notamment en cas d’incendie. Le but de l’exercice est d’étudier les impacts de foudre détectés par un capteur. 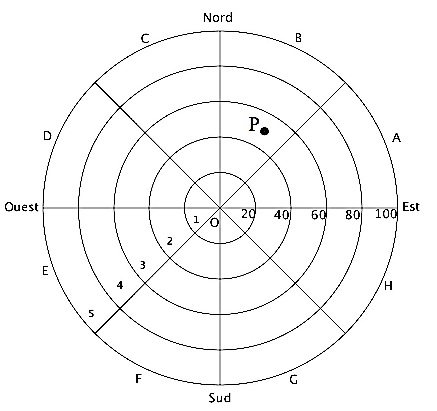L’écran radar, sur lequel les points d’impact de foudre sont observés, a l’allure suivante : Le capteur de foudre étant représenté par le centre de l’écran, cinq cercles concentriques correspondant aux rayons respectifs 20, 40, 60, 80 et 100 kilomètres délimitent dans l’ordre cinq zones, numérotées de 1 à 5, définies par leur distance au capteur. De plus, huit segments partant du capteur délimitent huit portions, de même ouverture angulaire, nommées dans le sens trigonométrique de A à H. L’écran est ainsi partagé en quarante secteurs dénommés par une lettre et un nombre entre 1 et 5. Par exemple, le point P positionné sur la figure est situé dans le secteur B3. On assimile l’écran radar à une partie du plan complexe en définissant un repère orthonormé (O; u, v) de la manière suivante : • l’origine O marque la position du capteur ; • l’axe des abscisses est orienté d’Ouest en Est ; • l’axe des ordonnées est orienté du Sud au Nord ; • l’unité choisie est le kilomètre. Dans la suite, un point de l’écran radar est associé à un point d’affixe z. Partie A. 1. On note zP l’affixe du point P situé dans le secteur B3 sur le graphique précédent. On appelle r le module de zP et q son argument dans l’intervalle ]-p ; +p]. Parmi les quatre propositions suivantes, déterminer la seule qui propose un encadrement correct pour r et pour q (aucune justification n’est demandée) : 40 < r <60 et p /4 < q < ½p. Proposition C. 2. Un impact de foudre est matérialisé sur l’écran en un point d’affixe z. Dans chacun des deux cas suivants, déterminer le secteur auquel ce point appartient : a. z = 70 e-t p/3. r =70 et q = -p/3. Secteur G4. b. z = -45 x3½ +45 i. r=[(-45 x3½)2 +452 ]½ =90 km. z / r = -3½/2 +i / 2 = cos(5p/6) + i sin (5p / 6) ; q = 5p /6. Secteur D5. Partie B. On suppose dans cette partie que le capteur affiche un impact au point P d’affixe 50eip/3. En raison d’imprécisions de mesures, le point d’impact affiché ne donne qu’une indication approximative du point d’impact réel de la foudre. Ainsi, lorsque le capteur affiche le point d’impact P d’affixe 50eip/3, l’affixe z du point d’impact réel de la foudre admet : • un module qui peut être modélisé par une variable aléatoire M suivant une loi normale d’espérance µ = 50 et d’écart type s = 5 ; • un argument qui peut être modélisé par une variable aléatoire T suivant une loi normale d’espérance p/3 et d’écart type p/12. On suppose que les variables aléatoires M et T sont indépendantes, c’est à dire que quels que soient les intervalles I et J, les événements (M appartient à I) et (T appartient à J) sont indépendants. Dans la suite les probabilités seront arrondies à 10-3 près. 1. Calculer la probabilité P(M< 0) et interpréter le résultat obtenu. La calculatrice donne P(M< 0) =0. Le module d'un nombre complexe ne peut pas être négatif. 2. Calculer la probabilité P(M appartient à ]40; 60[ ). P(M inférieur à 40 ) = 0,02275 ; P(M inférieur à 60 ) = 0,97725 ; P(M appartient à ]40; 60[ ) =0,97725-0,02275 ~0,954. 3. On admet que : P(T apartient à ] p/4 ; p /2[ )=0,819. En déduire la probabilité que la foudre ait effectivement frappé le secteur B3 selon cette modélisation.. Les événements (M appartient à I) et (T appartient à J) sont indépendants. P(la foudre frappe le secteur B3) = P(T apartient à ] p/4 ; p /2[ ) x P(M appartient à ]40; 60[ ) P(la foudre frappe le secteur B3) =0,819 x 0,954 =0,781. Exercice 4. On étudie un modèle de propagation d’un virus dans une population, semaine après semaine. Chaque individu de la population peut être, à l’exclusion de toute autre possibilité : • soit susceptible d’être atteint par le virus, on dira qu’il est « de type S » ; • soit malade (atteint par le virus) ; • soit immunisé (ne peut plus être atteint par le virus). Un individu est immunisé lorsqu’il a été vacciné, ou lorsqu’il a guéri après avoir été atteint par le virus. Pour tout entier naturel n, le modèle de propagation du virus est défini par les règles suivantes : • Parmi les individus de type S en semaine n, on observe qu’en semaine n + 1 : 85 % restent de type S, 5 % deviennent malades et 10 % deviennent immunisés ; • Parmi les individus malades en semaine n, on observe qu’en semaine n+ 1 : 65 % restent malades, et 35 % sont guéris et deviennent immunisés. • Tout individu immunisé en semaine n reste immunisé en semaine n + 1. On choisit au hasard un individu dans la population. On considère les événements suivants : Sn : « l’individu est de type S en semaine n » ; Mn : « l’individu est malade en semaine n » ; In : « l’individu est immunisé en semaine n ». En semaine 0, tous les individus sont considérés « de type S », on a donc les probabilités suivantes : P (S0)= 1, P(M0) = 0 et P(I0) = 0. Partie A. On étudie l’évolution de l’épidémie au cours des semaines 1 et 2. 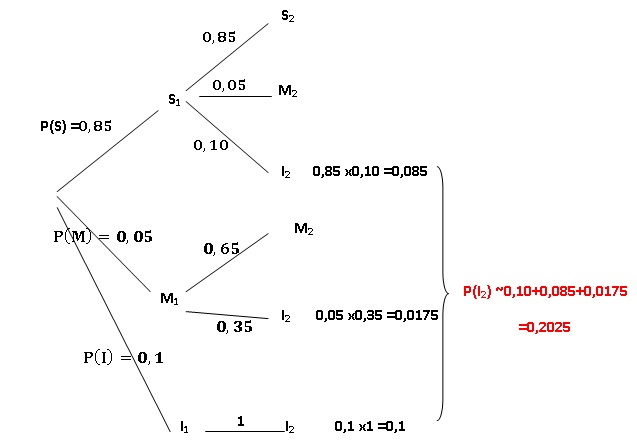1. Reproduire sur la copie et compléter l’arbre de probabilités donné ci-dessous. 2. Montrer que P(I2) = 0,2025. 3. Sachant qu’un individu est immunisé en semaine 2, quelle est la probabilité, arrondie au millième, qu’il ait été malade en semaine 1 ? PI2(M1) = P(I2 n M1) / P(I2) = 0,05 x0,35 / 0,2025 = 7 / 81 ~0,086. Partie B. On étudie dans cette partie l’évolution à long terme de l’épidémie. Pour tout entier naturel n, on note un = P(Sn) , vn = P(Mn) et wn=P(In) les probabilités respectives des événements Sn, Mn et In. 1. Justifier que, pour tout entier naturel n, on a : un + vn + wn = 1. Chaque semaine un individu est soit de type S, soit malade , soit immunisé.. P(Sn) +P(Mn) +P(In) = 1 ; soit un + vn + wn = 1. On admet que la suite (vn) est définie par v0 = 0 et, pour tout entier naturel n : vn+1 = 0,65vn + 0,05un. 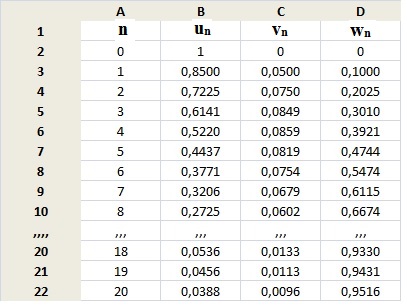2. À l’aide d’un tableur, on a calculé les premiers termes des suites (un), (vn) et (wn) : Pour répondre aux questions a et b suivantes, on utilisera la feuille de calcul reproduite ci-dessus. a. Quelle formule, saisie dans la cellule C3, permet, par recopie vers le bas, de calculer les termes de la suite (vn) ? =0,65*C2+0,05*B2 b. On admet que les termes de (vn) augmentent, puis diminuent à partir d’un certain rang N, appelé le « pic épidémique » : c’est l’indice de la semaine pendant laquelle la probabilité d’être malade pour un individu choisi au hasard est la plus grande. Déterminer la valeur du pic épidémique prévue par le modèle. v3=0,0849 ; v4 =0,0859 ; N = 4 ;v5 =0,0819. 3. a. Justifier que, pour tout entier naturel n, on a : un+1 = 0,85 un. En déduire l’expression de un en fonction de n. Parmi les individus de type S en semaine n, on observe qu’en semaine n + 1 : 85 % restent de type S. Donc un+1 = 0,85 un. La suite (un) est géométrique de raison 0,85 et de premier terme u0 =1. un = u0 x0,85n=0,85n. b. Montrer, à l’aide d’un raisonnement par récurrence, que pour tout entier naturel n on a : vn = 0,25(0,85n-0,65n). Initialisation : v0=0 ; u0 =1 ; v1 = 0,65v0 + 0,05u0 =0,05 ;  v0 = 0,25(0,850-0,650)=0,25 x 0 = 0.  v1 = 0,25(0,851-0,651)=0,25 x0,20 = 0,05. La propriété est vraie au rang 0 et au rang 1. Hérédité : on suppose la propriété vraie au rang n ; vn = 0,25(0,85n-0,65n). vn+1 = 0,65vn + 0,05un = 0,65 x0,25(0,85n-0,65n)+0,05 x0,85n. vn+1=0,25 [0,65 x 0,85n-0,65n+1)+0,85n /5]. 0,65+1/5 = 0,85 ; 0,65 x 0,85n+0,85n /5=0,85 x0,85n = 0,85n+1. Conclusion : la propriété est vraie au rang zéro et héréditaire. Elle est donc vraie pour tout entier n. 4. Calculer les limites de chacune des trois suites (un), (vn) et (wn). Que peut-on en déduire quant à l’évolution de l’épidémie prévue à long terme par ce modèle ? -1 <0,85 <1, donc la limite quand n tend vers l'infini de 0,85n est égale à zéro. -1 <0,65 <1, donc la limite quand n tend vers l'infini de 0,65n est égale à zéro. Donc un et vn tendent vers zéro quand n tend vers l'infini. or un +vn +wn = 1. Donc wn tend vers un quand n tend vers l'infini. A long terme tous les individus seront immunisés d'après ce modèle.

menu