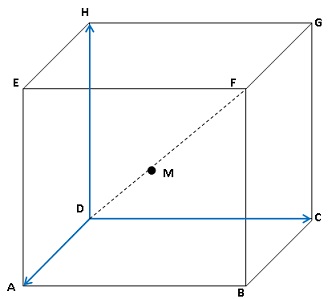
Mathématiques : loi normale, fonction, géométrie, cube. Bac S Liban 2017 . En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Exercice 1. On considère un cube ABCDEFGH dont la représentation en perspective cavalière est donnée ci-dessous. Les arêtes sont de longueur 1. L’espace est rapporté au repère orthonormé.   Partie A. 1. Montrer que le vecteur DF est normal au plan (EBG). 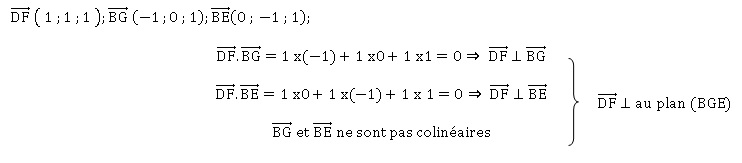2. Déterminer une équation cartésienne du plan (EBG). x+y+z+d=0. Le point E(1 ; 0 ; 1) appartient à ce plan : 1+0+1+d=0 soit d = -2. x+y+z-2=0. 3. En déduire les coordonnées du point I intersection de la droite (DF) et du plan (EBG). Equation paramétrique de la droite (DF) : x = t +xD = t ; y =t+yD = t ; z = t +zD = t. I appartient à la droite (DF)  et au plan(EBG) : t+t+t-2 = 0 soit t = 2/3. I(2/3 ; 2/3 ; 2/3). On démontrerait de la même manière que le point J intersection de la droite (DF) et du plan (AHC) a pour coordonnées J(1/3 ; 1/3 ; 1/3). .Partie B. 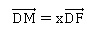À tout réel x de l’intervalle [0 ; 1], on associe le point M du segment [DF] tel que  On s’intéresse à l’évolution de la mesure q en radian de l’angle EMB lorsque le point M parcourt le segment [DF]. On a 0 < q < p. 1. Que vaut q si le point M est confondu avec le point D ? avec le point F ? M confondu avec D : le triangle EDB est équilatéral : les trois côtés sont égaux à la diagonale d'un carré de côté 1. q = p/3. M confondu avec F : q = p/2. 2.a) Justifier que les coordonnées du point M sont (x ;x ;x). Equation paramétrique de la droite (DF) : x=t ; y = t ; z = t. M appartient à cette droite : xM = yM =zM = t. b) Montrer que cos(q) =(3x2-4x+1) / (3x2-4x+2) . 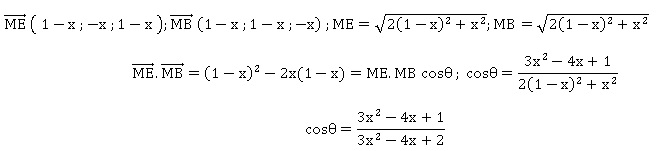3. On a construit ci-dessous le tableau de variations de la fonction f(x) =(3x2-4x+1) / (3x2-4x+2). 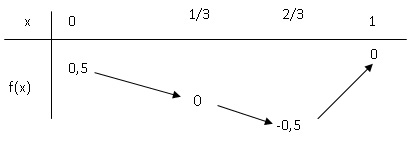Pour quelles positions du point M sur le segment [DF] : a) le triangle MEB est-il rectangle en M ? cosq = 0 ; 3x2-4x+1=0 ; D = 16-12=4 ; x1 =(4+2)/2=1 ; M confondu avec F.  x2=(4-2)/6=1/3. M est confondu avec J. b) l’angle q est-il maximal ? q est maximal quand cos q est minimal ; f(x) est minimal pour x = 2/3 ; M est en I. . . .... ..... Exercice 2. Dans cet exercice, on étudie quelques grandeurs caractéristiques du fonctionnement des parkings d’une ville. Dans tout l’exercice, les probabilités seront données avec une précision de 10-4. Partie A.Durée d’attente pour entrer dans un parking souterrain. On appelle durée d’attente le temps qui s’écoule entre le moment où la voiture se présente à l’entrée du parking et le moment où elle franchit la barrière d’entrée du parking. Le tableau suivant présente les observations faites sur une journée. Durée (min) [0 ; 2[ [2 ; 4[ [4 ; 6[ [6 ; 8[ Nombre de voitures 75 19 10 5 1. Proposer une estimation de la durée d’attente moyenne d’une voiture à l’entrée du parking. (75 +3 x19 +5 x10 +7 x5) / (75 +19 +10 +5) =217 /109 ~1,991 min. 2. On décide de modéliser cette durée d’attente par une variable aléatoire T suivant une loi exponentielle de paramètre  l (exprimé en minute). a) Justifier que l’on peut choisir l= 0,5 min. l=1/1,991 =109 / 217 ~0,50 min. b) Une voiture se présente à l’entrée du parking. Quelle est la probabilité qu’elle mette moins de deux minutes pour franchir la barrière ? P(T < 2)=1- exp(-0,50 x2) =0,6321. c) Une voiture attend à l’entrée du parking depuis une minute.Quelle est la probabilité qu’elle franchisse la barrière dans la minute suivante ? La loi exponentielle est sans mémoire ; P(T < 1)=1- exp(-0,50 ) =0,3935. Partie B - Durée et tarifs de stationnement dans ce parking souterrain. Une fois garée, la durée de stationnement d’une voiture est modélisée par une variable aléatoire D qui suit la loi normale d’espérance µ= 70 min et d’écart-type s= 30 min. 1.a) Quelle est la durée moyenne de stationnement d’une voiture ? 70 min. b) Un automobiliste entre et se gare dans le parking. Quelle est la probabilité que sa durée de stationnement dépasse deux heures ? P(D >120) = 1-P(D<120) = 1-0,9522 =0,0478. c) À la minute près, quel est le temps maximum de stationnement pour au moins 99 % des voitures ? La touche inverse loi normale de la calculatrice donne 140 min. 2. La durée de stationnement est limitée à trois heures. Le tableau donne le tarif de la première heure et chaque heure supplémentaire est facturée à un tarif unique. Toute heure commencée est due intégralement. Durée Inférieure à 15 min Entre 15 min et 1 heure heure supplémentaire Tarif (€) Gratuit 3,5 t Déterminer le tarif t de l’heure supplémentaire que doit fixer le gestionnaire du parking pour que le prix moyen de stationnement d’une voiture soit de 5 euros. P(D < 15) = 0,033376. P(15 < D < 60) =P(D <60) -P(D <15)=0,36944-0,033376=0,33606. P(60 < D < 120) =P(D <120) -P(D <60)=0,95221-0,36944=0,5828. P(120 < D < 180) =P(D <180) -P(D <120)=0,99988-0,95221=0,04466. E(D) = 5 = 0,33606 x 3,5 +0,5828( 3,5+t) +0,04466(3,5 +2t). 5 =1,176 +2,040 +0,1563 +0,67212 t. 1,627 =0,67212 t ; t = 2,42 €. Partie C.Temps d’attente pour se garer dans un parking de centre-ville La durée de stationnement d’une voiture dans un parking de centre-ville est modélisée par une variable aléatoire T ' qui suit une loi normale d’espérance µ' et d’écart-type s'. On sait que la moyenne du temps de stationnement dans ce parking est égale à 30 minutes et que 75% des voitures ont un temps de stationnement inférieur à 37minutes. Le gestionnaire du parking vise l’objectif que 95 % des voitures aient un temps de stationnement entre 10 et 50 minutes. Cet objectif est-il atteint ? µ' = 30 et P(T ' < 37) = 0,75. On pose X = ( T '-30) / s' =7 / s' suit la loi normale centrée réduite. P(X < 7 / s')=0,75 ; 7 / s' =0,675 ; s' = 7 /0,675 ~10,4. P( 10 < T ' < 50) = P(T '  < 50) -P(T ' < 10) =0,945, inférieur à 0,95.. L'objectif n'est pas atteint. Exercice 3. Soit k un réel strictement positif. On considère les fonctions fk définies sur R par : fk(x) = x +k e-x . On note Ck la courbe représentative de la fonction fk dans un plan muni d’un repère orthonormé. On a représenté ci-dessous quelques courbes Ck pour différentes valeurs de k. 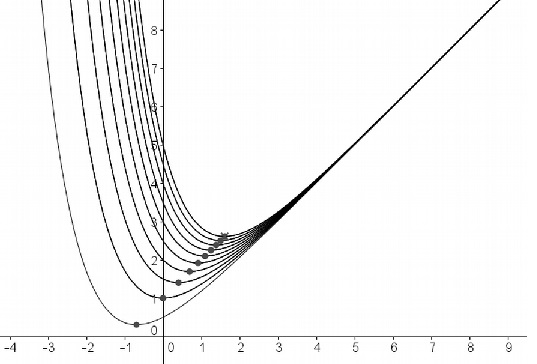Pour tout réel k strictement positif, la fonction fk admet un minimumsur R. La valeur en laquelle ce minimum est atteint est l’abscisse du point noté Ak de la courbe Ck. Il semblerait que, pour tout réel k strictement positif, les points Ak soient alignés. Est-ce le cas ? f 'k =1 -ke-x =0 ; ex = k ; x = ln k. fk (ln k) = lnk +1. Coordonnées des points Ak : (ln k ; ln k+1). Ces points appartiennent à la droite d'équation y = x+1. Ils sont donc alignés. Exercice 4. L’épicéa commun est une espèce d’arbre résineux qui peut mesurer jusqu’à 40 mètres de hauteur et vivre plus de 150 ans. L’objectif de cet exercice est d’estimer l’âge et la hauteur d’un épicéa à partir du diamètre de son tronc mesuré à 1,30 m du sol. Partie A -Modélisation de l’âge d’un épicéa Pour un épicéa dont l’âge est compris entre 20 et 120 ans, on modélise la relation entre son âge (en années) et le diamètre de son tronc (en mètre) mesuré à 1,30 m du sol par la fonction f définie sur l’intervalle ]0 ;1[ par : f (x) = 30ln((20x) / (1-x)) où x désigne le diamètre exprimé en mètre et f (x) l’âge en années. 1. Démontrer que la fonction f est strictement croissante sur l’intervalle ]0 ;1[. On pose u = 20 x et v = 1-x ; u' = 20 ; v' = -1 ; (u'v-v'u) /v2 =(20(1-x)+20x) /  (1-x)2=20 / (1-x)2. f '(x) =30 [20 / (1-x)2.] / [20x) / (1-x ] =30 /((1-x)x). x étant compris entre ]0 ;1[., f 'x) est positive sur cet intervalle ; f(x) est strictement croissante sur cet intervalle. 2. Déterminer les valeurs du diamètre x du tronc tel que l’âge calculé dans ce modèle reste conforme à ses conditions de validité, c’est-à-dire compris entre 20 et 120 ans. 20 = 30 ln(20x /(1-x)) ; e2/3 = 20x /(1-x) ; e2/3 (1-x)= 20x. x(20 e-2/3+1)=1 ; x = 1 / (20 e-2/3+1) =0,0887 ~0,09 m. 120 = 30 ln(20x /(1-x)) ; e4 = 20x /(1-x) ; e4 (1-x)= 20x. x(20 e-4+1)=1 ; x = 1 / (20 e-4+1) =0,7318 ~0,74 m. Le diamètre doit être compris entre 0,09 m et 0,73 m. Partie B. On a relevé la hauteur moyenne des épicéas dans des échantillons représentatifs d’arbres âgés de 50 à 150 ans. Le tableau suivant, réalisé à l’aide d’un tableur regroupe ces résultats et permet de calculer la vitesse de croissance moyenne d’un épicéa. A B C D E F G H I J K L M 1 Ages ( années) 50 70 80 85 90 95 100 105 110 120 130 150 2 Hauteur (m) 11,2 15,6 18,05 19,3 20,55 21,8 23 24,2 25,4 27,6 29,65 33 3 Vitese de croissance m/années 0,22 0,245 0,25 0,25 0,25 0,24 0,24 0,24 0,22 0,225 0,17 1.a) Interpréter le nombre 0,245 dans la cellule D3. Chaque année de la période  [70 ; 80ans ), la hauteur croît de 0,245 m b) Quelle formule doit-on entrer dans la cellule C3 afin de compléter la ligne 3 en recopiant la cellule C3 vers la droite ? =(C2-B2)/(C1-B1) 2. Déterminer la hauteur attendue d’un épicéa dont le diamètre du tronc mesuré à 1,30 m du sol vaut 27 cm. f (0,27) = 30ln((20x0,27) / (1-0,27))~60 ans. Entre 50 et 70 ans la hauteur croît de 0,22 m par an. 11,2 +10 x0,22=13,4 m. 3. La qualité du bois est meilleure au moment où la vitesse de croissance est maximale. a) Déterminer un intervalle d’âges durant lequel la qualité du bois est la meilleure en expliquant la démarche. On complète le tableau ci-dessus. la croissance est maximale entre 80 et 95 ans. b) Est-il cohérent de demander aux bûcherons de couper les arbres lorsque leur diamètre mesure environ 70 cm ? f (0,7) = 30ln((20x0,7) / (1-0,7))~115 ans. La vitesse de croissance n'est plus maximale ; la qualité du bois n'est plus la meilleure. Il est cohérent de couper ces arbres. .

menu