Mathématiques, nombres complexes, bac S 2017 .

Mathématiques, nombres complexes , bac S 2017 .

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

Antilles
On muni le plan complexe d'un repère orthonormé direct. On considère l'équation (E) :
z⁴ +2z³ -z-2=0
ayant pour inconnue le nombre complexe z.
1. Donner une solution entière de (E).

1⁴+2 x1³ -1-2 = 0 est vérifiée.z = 1.
2. Démontrer que pour tout complexe z :
z⁴ +2z³ -z-2=(z²+z-2)(z²+z+1).
(z²+z-2)(z²+z+1)= z⁴ +z³+z²+z³ +z²+z-2z²-2z-2 = z⁴ +2z³ -z-2.
3. Résoudre (E) dans l'ensemble des nombres complexes.
z²+z-2=0 ; discriminant D =1²+4 x 2=9 ; racine carrée du discriminant : 3.
Solutions z₁ = (-1+3) / 2 =1 et z₂ =(-1-3)/2 = -2.
z²+z+1=0 ; discriminant D =1²-4 =-3 =3i² ; racine carrée du discriminant : 3^½i.
Solutions z₃ = (-1+3^½i) / 2 et z₄ =(-1-3^½i)/2 .
4. Les solutions de l'équation (E) sont les affixes de 4 points A, B, C, D du plan complexe tes que ABCD est un quadrilatère non croisé.
Le quadrilatère est-il un losange ? Justifier.
Soient Les pointys :
A d'affixe 1, B d'affixe (-1+3^½i) / 2, C d'affixe -2 et D d'affixe (-1-3^½i) / 2.
Les nombres complexes (-1+3^½i) / 2 et (-1-3^½i) / 2 sont conjugués ; donc la droite (BD) est perpendiculaire à l'axe des réels.
Les nombres complexes 1 et -2 appartiennent à l'axe des réels ; donc la droite (AC) est perpendiculaire à la droite (BD).
Les diagonales du quadrilatère ABCD sont perpendiculaires.
Affixe du milieu du segment [AC] : [(-1+3^½i) / 2 +(-1-3^½i) / 2] / 2 = -0,5.
Affixe du milieu du segment [BD] : (1-2) / 2 = -0,5.
Les diagonales du quadrilatère se coupent en leur milieu.
Le quadrilatère ABCD est donc un losange.

.
.

....

.....
Métropole.
Dans une vaste plaine, un réseau de capteurs permet de détecter la foudre et de produire une image des phénomènes orageux. Ces données servent en particulier aux services météorologiques pour améliorer leurs prévisions et pour permettre des interventions plus rapides sur les lieux, notamment en cas d’incendie.
Le but de l’exercice est d’étudier les impacts de foudre détectés par un capteur.
L’écran radar, sur lequel les points d’impact de foudre sont observés, a l’allure suivante :

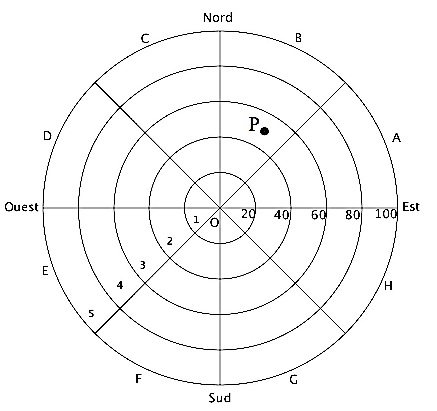
Le capteur de foudre étant représenté par le centre de l’écran, cinq cercles concentriques
correspondant aux rayons respectifs 20, 40, 60, 80 et 100 kilomètres délimitent dans l’ordre cinq
zones, numérotées de 1 à 5, définies par leur distance au capteur. De plus, huit segments partant du capteur délimitent huit portions, de même ouverture angulaire, nommées dans le sens
trigonométrique de A à H.
L’écran est ainsi partagé en quarante secteurs dénommés par une lettre et un nombre entre 1 et 5. Par exemple, le point P positionné sur la figure est situé dans le secteur B3.
On assimile l’écran radar à une partie du plan complexe en définissant un repère orthonormé (O; u, v) de la manière suivante :
• l’origine O marque la position du capteur ;
• l’axe des abscisses est orienté d’Ouest en Est ;
• l’axe des ordonnées est orienté du Sud au Nord ;
• l’unité choisie est le kilomètre.
Dans la suite, un point de l’écran radar est associé à un point d’affixe z.
Partie A.
1. On note z_P l’affixe du point P situé dans le secteur B3 sur le graphique précédent. On appelle r
le module de z_P et q son argument dans l’intervalle ]-p ; +p].
Parmi les quatre propositions suivantes, déterminer la seule qui propose un encadrement correct
pour r et pour q (aucune justification n’est demandée) :
40 < r <60 et p /4 < q < ½p. Proposition C.
2. Un impact de foudre est matérialisé sur l’écran en un point d’affixe z. Dans chacun des deux cas
suivants, déterminer le secteur auquel ce point appartient :
a. z = 70 e^{-t p/3}.
r =70 et q = -p/3. Secteur G4.
b. z = -45 x3^½ +45 i.
r=[(-45 x3^½)² +45² ]^½ =90 km.
z / r = -3^½/2 +i / 2 = cos(5p/6) + i sin (5p / 6) ; q = 5p /6. Secteur D5.

Métropole septembre.
Le plan complexe est rapporté à un repère orthonormé. À tout point M d’affixe z, on associe le
point M′ d’affixe z'= −z² + 2z. Le point M′ est appelé image du point M.
1. Résoudre dans l’ensemble C des nombres complexes l’équation : −z² + 2z − 2 = 0..
En déduire les affixes des points dont l’image est le point d’affixe 2.
Discriminant D =2²-4(-2)(-1) =-4 = 4 i².
z₁ = (-2 +2i)/(-2) = 1-i ; z₂ = 1+i.Les points dont l'image est le point d'affixe 2 vérifient :
z'=2 = -z²+2z soit -z²+2z-2=0.
Ce sont les points d'affixe 1+i et 1-i.
2. Soit M un point d’affixe z et M′ son image d’affixe z′.
On note N le point d’affixe z_N = z².
Montrer que M est le milieu du segment [NM′].
Soit P le milieu du segment [NM'] ; l'affixe de P est :
z_P = (z_N +z_M') / 2 = (z²−z² + 2z) /2 = z.
Donc M est le milieu du segment [NM′].
3. Dans cette question, on suppose que le point M ayant pour affixe z, appartient au cercle C de centre O et de rayon 1. On note q un argument de z.
a. Déterminer le module de chacun des nombres complexes z et z_N, ainsi qu’un argument de z_N en
fonction de q.
Module de z : |z| = 1. Argument de z : q ; z = 1 exp(iq).
z_N = z² = 1 exp(2iq).
Le module de z_N vaut 1 et son argument 2q.
b. Sur la figure donnée ci-dessous, on a représenté un point M sur le cercle C.
Construire sur cette figure les points N et M′ en utilisant une règle et un compas (on laissera les traits de construction apparents).

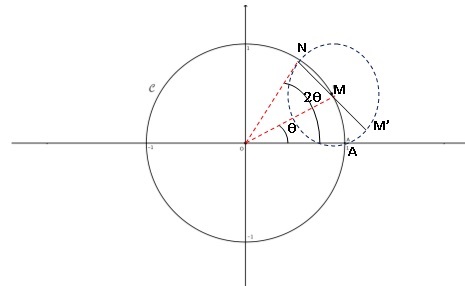
c. Soit A le point d’affixe 1. Quelle est la nature du triangle AMM′ ?
M est le milieu du segment [NM'] ; MN=MM'.
N appartient au cercle de centre M et de rayon MA. ; MA = MN.
Par suite, MA = MM'; le triangle AMM' est isocèle en M. .

Nlle Calédonie
Les questions 1. et 2. de cet exercice pourront être traitées de manière indépendante.
On considère la suite des nombres complexes (z_n) définie pour tout entier naturel n par
z_n =(1+i) / (1−i)ⁿ .
On se place dans le plan complexe d’origine O.
1. Pour tout entier naturel n, on note A_n le point d’affixe z_n.
a. Démontrer que, pour tout entier naturel n,
z_n+4/z_nest réel.
Soit le nombre complexe 1+i ; son module est égal à 2^½ et son argument vaut p/4.
Soit le nombre complexe 1-i ; son module est égal à 2^½ et son argument vaut -p/4.
Soit le nombre complexe (1-i)ⁿ ; son module est égal à 2^½n et son argument vaut -np/4.
Soit le nombre complexe z_n ; son module est égal à 2^½(1-n) et son argument vaut (n+1)p/4.
Soit le nombre complexe z_n+4 ; son module est égal à 2^½(1-n-4) et son argument vaut (n+4+1)p/4.
Soit le nombre complexe z_n+4/z_n ; son module est égal à 2^½(1-2n-4) et son argument vaut (n+4+1-n-1)p/4 soit.p.

b. Démontrer alors que, pour tout entier naturel n, les points O, A_n et A_n+4 sont alignés.

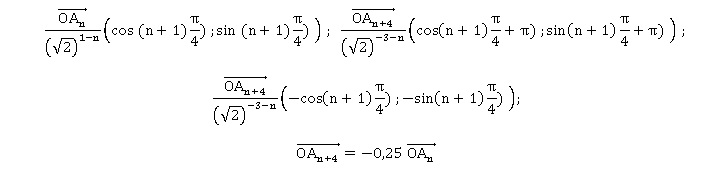
2. Pour quelles valeurs de n le nombre z_n est-il réel ?
L'argument de z_n doit être un multiple de p.
(n+1)p/4 = k p avec k entier positif.
n+1 = 4 k ; n = 4k-1.

Amérique du Sud
Dans le plan complexe muni d’un repère orthonormé direct ; on considèreles points A et B d’affixes respectives
z_A = 2e^{iπ / 4}et z_B = 2e^{i 3π / 4}.
1. Montrer que OAB est un triangle rectangle isocèle.
OA = 2 ; OB = 2. Le triangle OAB est isocèle en O.

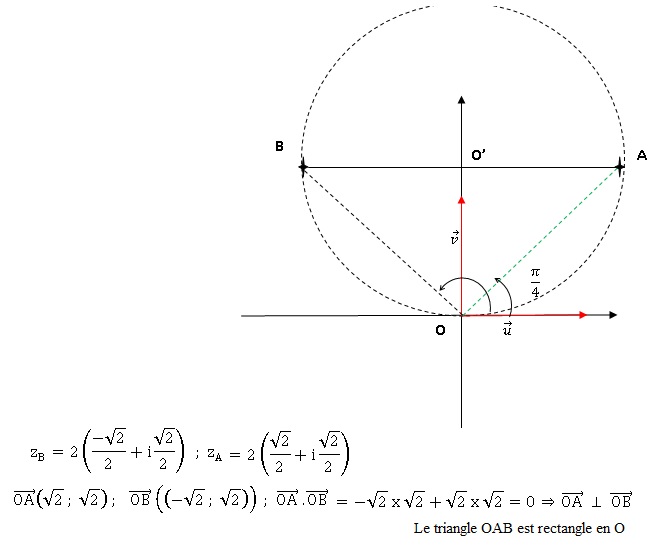
2. On considère l’équation (E) : z² −6^½z +2 = 0.
Montrer qu’une des solutions de (E) est l’affixe d’un point situé sur le cercle circonscrit au triangle OAB.
Equation du cercle circonscrit au triangle OAB ( centre O' (0 ; 2^½) et rayon R = O'A = 2^½ cm).
x² +(y-2^½)² =2.
Solutions de (E) : D = 6-4 x2 = -2 = 2 i².

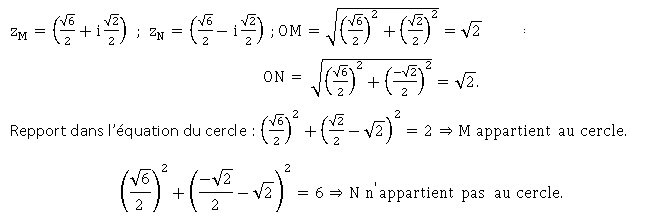
menu