Mathématiques,
suites, algorithme , bac S 2017 .
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Liban
Soit
k un réel strictement positif. On considère les fonctions fk
définies sur R par :
fk(x) = x +k e-x .
On note Ck la courbe représentative de la fonction fk
dans un plan muni d’un repère orthonormé.
On a représenté ci-dessous quelques courbes Ck pour
différentes valeurs de k.
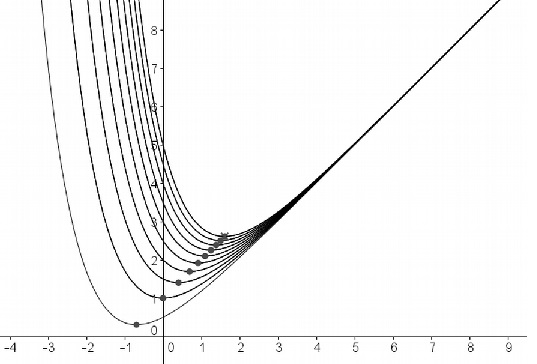
Pour tout réel k strictement positif, la fonction fk admet
un minimumsur R. La valeur en laquelle
ce minimum est atteint est l’abscisse du point noté Ak de la
courbe Ck. Il semblerait que, pour
tout réel k strictement positif, les points Ak soient
alignés. Est-ce le cas ?
f 'k =1 -ke-x =0 ; ex = k ; x = ln k.
fk (ln k) = lnk +1.
Coordonnées des points Ak : (ln k ; ln k+1).
Ces points appartiennent à la droite d'équation y = x+1. Ils sont donc
alignés.
Exercice 4.
L’épicéa commun est une espèce d’arbre résineux qui peut mesurer
jusqu’à 40 mètres de hauteur
et vivre plus de 150 ans. L’objectif de cet exercice est d’estimer
l’âge et la hauteur d’un épicéa à partir du diamètre de son tronc
mesuré à 1,30 m du sol.
Partie A
-Modélisation de l’âge d’un épicéa
Pour un épicéa dont l’âge est compris entre 20 et 120 ans, on modélise
la relation entre son âge (en
années) et le diamètre de son tronc (en mètre) mesuré à 1,30 m du sol
par la fonction f définie sur
l’intervalle ]0 ;1[ par : f (x) = 30ln((20x) / (1-x))
où x désigne le diamètre exprimé en mètre et f (x) l’âge en années.
1. Démontrer que la
fonction f est strictement croissante sur l’intervalle ]0 ;1[.
On pose u = 20 x et v = 1-x ; u' = 20 ; v' = -1 ; (u'v-v'u) /v2
=(20(1-x)+20x) / (1-x)2=20 / (1-x)2.
f '(x) =30 [20
/ (1-x)2.]
/ [20x)
/ (1-x ] =30 /((1-x)x).
x étant compris entre ]0 ;1[., f 'x) est positive sur cet
intervalle ; f(x) est strictement croissante sur cet intervalle.
2.
Déterminer les valeurs du diamètre x du tronc tel que l’âge calculé
dans ce modèle reste conforme à ses conditions de validité,
c’est-à-dire compris entre 20 et 120 ans.
20 = 30 ln(20x /(1-x)) ; e2/3 =
20x /(1-x) ; e2/3 (1-x)= 20x.
x(20 e-2/3+1)=1 ; x = 1 / (20 e-2/3+1)
=0,0887 ~0,09 m.
120 = 30
ln(20x /(1-x)) ; e4 = 20x /(1-x) ; e4
(1-x)= 20x.
x(20 e-4+1)=1 ; x = 1 / (20
e-4+1) =0,7318 ~0,74 m.
Le diamètre doit être compris entre 0,09 m et 0,73 m.
|
| .
. |
....
.....
|
Amérique du Nord.
Le
but de cet exercice est d’étudier les suites de termes positifs dont
le premier terme u0 est strictement supérieur à 1 et
possédant la propriété suivante : pour tout entier naturel n > 0, la
somme des n premiers termes consécutifs est égale au produit des n
premiers termes consécutifs. On admet qu’une telle suite existe et on
la note (un). Elle vérifie donc trois propriétés :
u0 > 1,
pour tout n >
0, un >
0.
pour tout n > 0, sn=u0 +u1+...+un-1= u0 xu1x...xun-1.
1. On choisit u0
= 3. Déterminer u1 et u2.
3+u1=3u1 ; u1=1,5.
3+1,5 +u2=3x1,5 u2
; u2=4,5 /3,5=9 / 7.
2.
a) Vérifier que
pour tout entier n > 0, sn+1 = sn +un
et sn > 1.
sn+1
=u0 +u1+...+un-1+un=sn +un.
sn+1 -sn =un avec un
>0.
sn+1 >sn , la
suite est croissante et le premier terme est strictement supérieur à 1.
b)
En déduire que pour tout entier n >0, un =sn /
(sn -1).
sn+1 =sn xun =sn +un ; un ((sn -1) =sn ; un =sn / (sn
-1).
c)
Montrer que pour tout n >
0 , un > 1.
sn >1, donc sn-1 >0. Par suite sn >sn-1.
Or un =sn / (sn
-1)>0.
3.
À l’aide de l’algorithme suivant, on veut calculer le terme un
pour une valeur de n donnée.
a) Recopier et
compléter la partie traitement de l’algorithme.
Entrée : saisir n ; saisir u.
Traitement : s prend la valeur u.
Pour i allant de 1 à n :
u prend la valeur s /(s-1)
s prend la valeur s+u
Fin pour
Sortie : afficher u.
b) Le tableau
ci-dessous donne des valeurs arrondies au millième de un
pour différentes
valeurs de l’entier n :
n
|
0
|
5
|
10
|
20
|
30
|
40
|
un
|
3
|
1,140
|
1,079
|
1,043
|
1,030
|
1,023
|
Quelle conjecture
peut-on faire sur la convergence
de la suite (un) ?
La suite (un) converge vers1.
4.a) Justifier que
pour tout entier n > 0, sn>n.
Initialisation
: s1=u0 >1. La propriété est vraie au rang 1.
Hérédité ;
on supose la propriété vraie au rang p : sp>p.
sp+1 = sp +up avec up >1.
sp +up > p+up
> p+1. La propriété est vraie au rang p+1.
Conclusion
: la propriété est vraie au rang 1 et héréditaire.
Donc
pour tout entier n > 0, sn>n.
b) En
déduire la limite de la suite (sn) puis celle de la suite (un).
Quand n tend vers l'infini, sn tend vers l'infini.
un = sn /
(sn -1) = 1 / (1 -1 /sn).
1
/sn tend vers zéro quand n tend vers l'infini. Donc un
tend vers 1
|
|
|
Centres
étrangers.
Partie C. Etude
de la suite (rn).
On considère la fonction f définie pour tout réel x de l'intervalle ]0
; p[ par f(x) = x / sin(x).
Ainsi rn = [1 /p
f(2p/n)]½.
On admet que f est strictement croissante sur ]0 ; p[.
Montrer que la suite (rn) est décroissante. On pourra
commencer par démontrer que pour n >4, 0 < 2p/(n+1) <p.
pour n >4, 0 < 2 < n < n+1 équivalent à : 0 <1
/ (n+1) < 1 / n < 0,5.
0 <2p
/ (n+1) < 2p / n < p.
f étant strictement croissante et strictement positive sur cet
intervalle : 0 <f(2p /
(n+1)) < f((2p / n).
0 < 1 / p
f(2p /
(n+1)) < 1 / p f((2p / n).
La fonction racine carrée est croissante sur [0 ; +oo[.
Par suite : 0 < [1 / p
f(2p /
(n+1))]½ < [1 / p f((2p / n)]½.
Soit 0 < rn+1 < rn. La suite (rn)
est donc décroissante.
2. En déduire que
cette suite converge. On ne demande pas de déterminer sa limite L et on
admet que L = p-½.
Cette suite est décroissante et de plus elle est
minorée par zéro. Cette suite converge donc.
3. On considère
l'algorithme suivant :
Variable : n est un nombre entier.
Traitement : n prend la valeur 4.
Tant que [2 / (n sin(2p
/n))]½ <0,58 faire
n prend la
valeur n+1
Fin Tant que
Sortie : Afficher n.
Quelle valeur numérique de n affiche cet algorithme ?
 . .
|
|
|
|
Métropole.
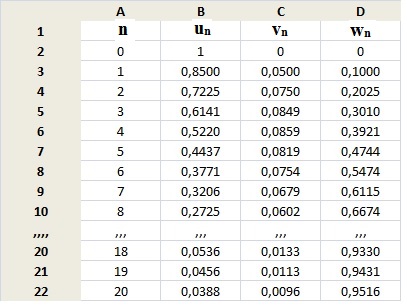
Pour
répondre aux questions a et b suivantes, on utilisera la feuille de
calcul reproduite ci-dessus.
a. Quelle formule, saisie dans la cellule C3,
permet, par recopie vers le bas, de calculer les termes de la suite (vn)
?
=0,65*C2+0,05*B2
b. On admet que les termes de (vn)
augmentent, puis diminuent à partir d’un certain rang N, appelé le «
pic épidémique » : c’est l’indice de la semaine pendant laquelle la
probabilité
d’être malade pour un
individu choisi au hasard est la plus grande.
Déterminer la valeur du
pic épidémique prévue par le modèle.
v3=0,0849
; v4 =0,0859 ; N = 4 ;v5 =0,0819.
3. a. Justifier que, pour tout entier naturel
n, on a : un+1 = 0,85 un.
En déduire l’expression
de un en fonction de n.
Parmi les
individus de type S en semaine n, on observe qu’en semaine n + 1 : 85 % restent de type S.
Donc un+1 = 0,85 un.
La suite (un) est géométrique de raison 0,85 et de premier
terme u0 =1.
un = u0 x0,85n=0,85n.
b. Montrer, à l’aide d’un
raisonnement par récurrence, que pour tout entier naturel n on a :
vn = 0,25(0,85n-0,65n).
Initialisation
: v0=0 ; u0 =1 ; v1 = 0,65v0 +
0,05u0 =0,05 ;
v0 = 0,25(0,850-0,650)=0,25 x 0 = 0.
v1 = 0,25(0,851-0,651)=0,25
x0,20 = 0,05.
La propriété est vraie au rang 0 et au rang 1.
Hérédité :
on suppose la propriété vraie au rang n ;
vn = 0,25(0,85n-0,65n).
vn+1
= 0,65vn + 0,05un = 0,65
x0,25(0,85n-0,65n)+0,05 x0,85n.
vn+1=0,25 [0,65 x 0,85n-0,65n+1)+0,85n
/5].
0,65+1/5 = 0,85 ; 0,65 x 0,85n+0,85n /5=0,85 x0,85n =
0,85n+1.
Conclusion
: la propriété est vraie au rang zéro et héréditaire. Elle est donc
vraie pour tout entier n.
4.
Calculer les limites de chacune des trois suites (un), (vn)
et (wn).
Que peut-on en déduire quant à l’évolution de l’épidémie prévue à long
terme par ce modèle ?
-1 <0,85 <1, donc la limite quand n tend vers l'infini de 0,85n
est égale à zéro.
-1 <0,65 <1, donc la limite quand n tend
vers l'infini de 0,65n est égale à zéro.
Donc un et vn tendent vers zéro quand n tend vers
l'infini.
or un +vn +wn = 1.
Donc wn tend vers un quand n tend
vers l'infini.
A long terme tous les individus seront immunisés d'après ce modèle.
|
Asie.
On considère la suite ( un) définie
par : u0 =1
et, pour tout entier naturel n, un+1 =(n+1) / (2n+4) un.
On définit la suite (vn ) par : vn =(n+1)un
pour tout entier naturel n,
1. La feuille de calcul
ci-dessous présente les valeurs des premiers termes des suites ( un)
et ( vn) , arrondies au
cent-millième.
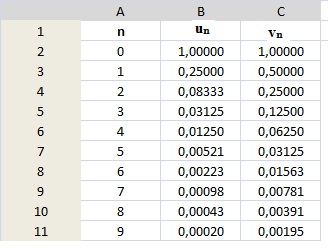
Quelle formule, étirée ensuite vers le bas, peut-on écrire dans la
cellule B3 de la feuille de calcul pour obtenir les
termes successifs de (un ) ?
=(A2+1)/(2*A2+4)*B2 ou =A3/(2*A2+4)*B2
2. a) Conjecturer l’expression de vn
en fonction de n .
vn = 0,5n.
b) Démontrer cette
conjecture.
Initialisation
: v0 = 0,50 = 1 ; v1 = 0,51
= 0,5 ; la propriété est vraie au rang zéro.
Hérédité :
on suppose la propriété vraie au rang p: vp = 0,5p.
vp+1 = (p+2)up+1 =(p+2)(p+1) / (2p+4) up =
(p+1) / 2 up=0,5 vp=0,5 x0,5p =0,5p+1.
La propriété est vraie au rang p+1.
Conclusion
: la propriété est vraie au rang zéro et héréditaire. Pout tout entier
n, vn = 0,5n.
3. Déterminer la limite de la suite
(un).
Pour tout entier n
: un = vn /(n+1) = 0,5n /(n+1).
0 < 0,5 <1, donc quand n tend vers l'infini, 0,5n tend
vers zéro.
1/(n+1) tend vers zéro quand n tend vers l'infini.
La limite de la suite (un) est égale
à zéro quand n tend vers l'infini.
L’objet du problème est l’étude des intégrales I et J définies
ci-dessous:
Partie A : valeur
exacte de l’intégrale I
1. Donner une
interprétation géométrique de l’intégrale I .
2. Calculer la
valeur exacte de I .
L'intégrale I est l'aire du domaine compris entre la courbe C
représentant la fonction f(x) = 1 / (1+x) , l'axe des abscisses et les
droites d'équation x=0 et x=1.
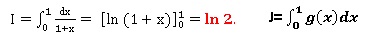
Partie B :
estimation de la valeur de J
Soit g la fonction définie sur l’intervalle [0;1] par g(x) = 1 / (1+x2).
On note Cg sa courbe représentative dans un repère
orthonormé du plan.
Le but de cette partie est d’évaluer l’intégrale J à l’aide de la
méthode probabiliste décrite ci-après.
On choisit au hasard un point M(x, y) en tirant de façon indépendante
ses coordonnées x et y au
hasard selon la loi uniforme sur [0;1] .
On admet que la probabilité p qu’un point tiré de cette manière soit
situé sous la courbe Cg est égale
à l’intégrale J.
En pratique, on initialise un compteur c à 0, on fixe un entier naturel
n et on répète n fois le processus suivant :
- on choisit au hasard et indépendamment deux nombres x et y, selon la
loi uniforme sur [0;1] ;
- si M(x, y) est au-dessous de la courbe Cg , on incrémente
le compteur c de 1.
On admet que f = c / n est une valeur approchée de J . C’est le
principe de la méthode dite de
Monte-Carlo.
Recopier et compléter l’algorithme ci-après pour qu’il affiche une
valeur approchée de J.
Variables : n, c, f, i, s, y sont des nombres.
Traitement :
lire la valeur de n
c prend la valeur 0
Pour i allant de 1 à n faire
x prend une valeur aléatoire entre 0 et 1
y prend une valeur aléatoire
entre 0 et 1
Si 1 /(1+x2) < y alors
c prend la valeur c+1
Fin Si
Fin pour
f prend la valeur c /n.
2.
Pour n =1000 , l’algorithme ci-dessus a donné pour résultat : f = 0,781.
Donner un intervalle de confiance, au niveau de confiance de 95 %, de
la valeur exacte de J.
n = 1000 > 30 ; nf
= 1000 x0,7881 = 781 >
5 ; n(1-f) = 1000 x0,219 = 219 > 5.
Les conditions sont remplies.
1 / n ½ =1 / 1000½ = 0,0316 ;
Intervalle de confiance ; [0,781 -0,0316 ; 0,781 +0,0316 } soit [0,749
; 0,813 ].
3. Quelle
doit-être, au minimum, la valeur de n pour que l’intervalle de
confiance, au niveau de
confiance de 95 %, ait une amplitude inférieure ou égale à 0,02 ?
Amplitude = 0,02 = 2 / n½
; n½ = 2 /0,02 = 100 ; n = 10 000.
Nlle Calédonie
Soit (un) la suite définie par u0 = 3, u1
=6 et, pour tout entier naturel n :
un+2 =5 /4un+1−1 /4un.
Le but de cet exercice est d’étudier la limite éventuelle de la suite (un).
Partie A :
On souhaite calculer les valeurs des premiers termes de la suite (un)
à l’aide d’un tableur.
On a reproduit ci-dessous une partie d’une feuille de calcul, où
figurent les valeurs de u0 et de u1.
|
A
|
B
|
1
|
n
|
un
|
2
|
0
|
3
|
3
|
1
|
6
|
4
|
2
|
6,750
|
5
|
3
|
6,938
|
6
|
4
|
6,984
|
7
|
5
|
6,996
|
1. Donner une
formule qui, saisie dans la cellule B4, puis recopiée vers le bas,
permet d’obtenir des valeurs de la suite (un) dans la
colonne B.
=5/4*B3-0,25*B2
2. Recopier et
compléter le tableau ci-dessus. On donnera des valeurs approchées à 10−3
près de un pour n allant de 2 à 5.
3. Que peut-on
conjecturer à propos de la convergence de la suite (un) ?
On conjecture que la suite (un)
converge vers 7.
Partie B :
Étude de la suite
On considère les suites (vn) et (wn) définies
pour tout entier naturel n par :
vn =un+1 −0,25 un et wn
=un −7.
1. a. Démontrer que
(vn) est une suite constante.
Initialisation : v0
=u1 −0,25 u0 = 6-0,75 =5,25.
v1 =u2
−0,25 u1 = 6,75-1,5 =5,25.
La propriété est vraie au rang 1.
Hérédité :
vp = vp+1 est supposée vraie.
vp+2= up+3−0,25
up+2 = 1,25up+2−0,25up+1 −0,25 up+2
vp+2= up+2−0,25up+1
=vp+1.
La propriété est vraie au rang p+1.
Conclusion :
la propriété est vraie au rang 1 et héréditaire, donc elle est vraie
pour tout n.
b. En déduire que, pour tout entier
naturel n, un+1 =0,25 un +21 / 4.
vn =un+1
−0,25 un = v0.
v0
=u1 −0,25 u0 =6-0,25x3=21 / 4.
Par
suite un+1 =0,25 un + 21 / 4.
2. a. En utilisant le résultat de la
question 1. b., montrer par récurrence que, pour tout entier naturel n, un <un+1
< 15.
Initialisation
: u0
<u1 < 15. La propriété est vraie au rang zéro.
Hérédité :
up <up+1 < 15 est
supposé vraie.
up+2= 0,25 up+1 +21 / 4.
up+2 < 0,25 x15 +21 / 4 ; up+2 < 0,25 x15 +21 / 4 ; up+2 < 9
soit up+2 < 15.
up+1= 0,25 up +21 /
4 ; up+1 < 0,25 x9 +21/4 ; up+1 < 30 / 4.
Par suite up+1 <up+2 < 15.
Conclusion
: la
propriété est vraie au rang 1 et héréditaire, donc elle est vraie pour
tout n.
b. En déduire que la suite (un)
est convergente.
un -un<un+1
-un< 15-un.
0 < un+1
-un< 15-un.
Or un est inférieur à 15, donc un+1 -un
>0.
La suite (un) est croissante et bornée par 15, donc elle
converge.
3. a. Démontrer que (wn) est une suite géométrique
dont on précisera le premier terme et
la raison.
wn
=un −7.
wn+1
=un+1 −7=0,25 un +21 / 4 -7 = 0,25 un -7 / 4
=0,25 (un-7) = 0,25 wn.
La suite est géométrique de raison q = 0,25.
w0 = u0-7 =3-7= -4.
b. En
déduire que, pour tout entier naturel n, un = 7−(1/4)n-1.
un =wn+7 ; wn = w0 x(1/4)n
= -4 x(1/4)n
; un =7 -4 x(1/4)n =7−(1/4)n-1.
c. Calculer la
limite de la suite (un).
-1 conséquent < 1/4 < 1 ; par (1/4)n-1 tend vers zéro quand n tend
vers l'infini.
La limite de la suite (un) est égale à 7.
Amérique du Sud
Un biologiste souhaite étudier
l’évolution de la population d’une
espèce animale dans une réserve.
Cette population est estimée à
12 000 individus en 2016. Les
contraintes du milieu naturel font que la population ne peut pas
dépasser les 60 000 individus.
Partie A : un
premier modèle.
Dans une première approche, le
biologiste estime que la population
croît de 5% par an.
L’évolution annuelle de la
population est ainsi modélisée par une suite
(vn)
où vn représente le nombre d’individus,
exprimé en milliers, en 2016+n. On a donc v0 = 12.
1. Déterminer la
nature de la suite (vn) et donner l’expression de vn
en fonction de n.
On passe d'un terme au suivant
en multipliant ce treme par 1,05. Il
s'agit d'une suite géométrique de raison 1,05 et de premier terme 12. vn = 12 x 1,05n.
2. Ce modèle
répond-il aux contraintes du milieu naturel ?
-1 < 1,05 < 1, donc 1,05n tend vers
l'infini quand n
tend vers l'infini.
La population dépassera les 60
000 individus en :
60 = 12 x1,05 n n= ln
(5) / ln(1,05) ~33
En 2016 +33 = 2049, la
population dépasse 60 000 individus.
Ce modèle ne convient pas.
Partie B : un
second modèle
Le biologiste modélise ensuite
l’évolution annuelle de la population
par une suite (un) définie par u0 = 12 et, pour
tout entier nature n, un+1 = −1,1 /605 u2n +1,1un
.
1. On considère la
fonction g définie sur R par g (x)= −1,1 /605 x2 +1,1x .
a. Justifier que g
est croissante sur [0; 60].
g'(x) = -2,2 / 605 x +1,1.
g'(x) = 0 pour x =302,5.
g'(x) est positive sur [0 ;
302,5[ et g(x) est donc strictement
croissante sur cet intervalle.
b. Résoudre dans R
l’équation g (x) = x.
−1,1 /605 x2
+1,1x = x.
−1,1
/605 x2 +0,1x =0.
x (0,1-1,1 / 605x) = 0.
x =0 ; x =60,5 /1,1 = 55.
2.
On remarquera que un+1 = g (un).
a. Calculer la
valeur arrondie à 10−3 de u1. Interpréter.
u1 = g(u0)= g(12)=
-1,1 / 605 x122+1,1
x12 ~12,938.
En 2017, la population
atteindra 12938 individus.
b. Démontrer
par
récurrence que, pour tout entier naturel n, 0 < un < 55.
Initialisation
: u0 =12. La propriété est vraie au rang zéro.
Hérédité :
on supose la propriété vraie au rang p : 0 < up < 55.
Par conséquence g(0) <
g(un) <
g(55), car g est croissante sur [0 ; 60 ].
0 < g(un)
< −1,1
/605 x552 +55 x1,1.
0 < g(un)
< −1,1
/605 x552 +55 x1,1.
0 < g(un)
< −5,5
+60,5.
0 < g(un)
< 55.
Conclusion :
la propriété est vraie au rang zéro et héréditaire, elle est vraie pour
tout entier n.
c. Démontrer que la
suite (un) est croissante.
un+1-un= g(un)-un.
un+1-un=−1,1 /605 u2n +0,1un.
un+1-un=un(−1,1 /605 un +0,1).
D'une part, un étant compris entre 0 et 55 est positif.
D'autre part, 0 <
un < 55
soit 0 > -1,1 / 605 un
> -1,1
/605 x55
0 > -1,1 / 605 un
> -0,1
0 +1,1> -1,1 / 605 un
+1,1 > -0,1+1,1
1,1 > -1,1 / 605 un +1,1 > 1, donc -1,1 / 605 un +1,1
est positif.
Par suite un+1-un est positif ; un+1
> un ; la suite (un) est croissante.
d. En déduire la
convergence de la suite (un).
La suite (un) est croissante et majorée par 55. Elle
converge donc vers l
< 55.
e. On admet que la
limite ℓ de la suite (un) vérifie g (ℓ) = ℓ. En déduire sa
valeur et l’interpréter dans le contexte de l’exercice.
g(l)=l ; la suite étant
croissante et son premier terme étant égal à 12, l = 55.
3. Le biologiste
souhaite déterminer le nombre d’années au bout duquel la population
dépassera les 50 000 individus avec ce second modèle.
Il utilise l’algorithme suivant.
Variables : n entier naturel
u réel
Traitement : n prend la valeur 0
u prend la valeur 12
Tant que u < 50
u prend la valeur −1,1 /605 u2+1,1u
n prend la valeur n+1
Fin Tant que.
Sortie : Afficher n
Recopier et compléter cet algorithme afin qu’il
affiche en sortie le plus petit entier r tel que ur >50.
|
|