Mathématiques,
probabilités, loi exponentielle, Bac S 2016
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Métropole.
Partie A.
Une usine fabrique un composant électronique. Deux chaînes de
fabrication sont utilisées.
La chaîne A produit 40% des composants et la chaîne B produit le reste.
Une partie des composants fabriqués présentent un défaut qui les
empêche de fonctionner à la vitesse prévue par le constructeur. En
sortie de chaîne A, 20% des composants présentent ce défaut alors qu’en
sortie de chaîne B, ils ne sont que 5%.
On choisit au hasard un composant fabriqué dans cette usine. On note :
A l’évènement « le composant provient de la chaîne A »
B l’évènement « le composant provient de la chaîne B »
S l’évènement « le composant est sans défaut »
1. Montrer que la
probabilité de l’évènement S est P(S) = 0,89.
Probabilité q'un composant issu de A ait un défaut :0,40 x0,20 =0,08.
Probabilité
q'un composant issu de B ait un défaut :0,60 x0,05 =0,03.
P(S)=1-0,08-0,03=0,89.
2. Sachant que le
composant ne présente pas de défaut, déterminer la probabilité qu’il
provienne de la chaîne A. On donnera le résultat à 10−2 près.
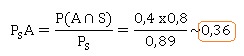
Partie B.
Des améliorations apportées à la chaîne A ont eu pour effet d’augmenter
la proportion p de composants sans défaut. Afin d’estimer cette
proportion, on prélève au hasard un échantillon de 400 composants parmi
ceux fabriqués par la chaîne A. Dans cet échantillon, la fréquence
observée de composants sans défaut est de 0,92.
1. Déterminer un
intervalle de confiance de la proportion p au niveau de confiance de
95%.
Taille de l'échantillon n = 400, supérieur
à 30.
Proportion de composants sans défaut p = 0,92 ; q = 1-p = 0,08.
np = 368, valeur supérieure à 5 ; nq = 32, valeur supérieure
à 5.
Les
conditions sont requises pour établir un intervalle de confiance de la
proportion p au seuil de 95 % de l'échantillon de taille n = 400.
1 / 400½= 0,05 ; intervalle de confiance [0,92 -0,05 ; 0,92
+0,05] soit [0,87 ; 0,97].
2.
Quelle devrait être la taille minimum de l’échantillon pour qu’un tel
intervalle de confiance ait une amplitude maximum de 0,02 ?
2
x(1/n)½ =0,02 ;(1/n)½ =0,01 ; 1/n = 10-4
; n=10000.
Partie C.
Loi exponentielle.
La durée de vie, en années, d’un composant électronique fabriqué dans
cette usine est une variable aléatoire T qui suit la loi exponentielle
de paramètre l (où
l est
un nombre réel strictement positif ). On note f la fonction densité
associée à la variable aléatoire T .
1. La courbe
représentative C de la fonction f est donnée ci-dessous.
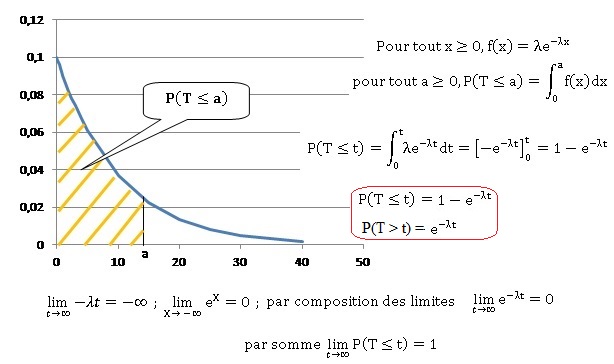 2.
On suppose que P(T <=7) = 0,5. Déterminer l à 10−3 près.
2.
On suppose que P(T <=7) = 0,5. Déterminer l à 10−3 près.
1-exp(-7 l)=0,5 ;
exp(-7
l)
=0,5 ; -7
l
=ln0,5 = -ln2 ; l = ln2 / 7 ~0,099.
3.
Dans cette question on prend λ = 0,099 et on arrondit les résultats des
probabilités au centième.
a. On choisit au
hasard un composant fabriqué dans cette usine. Déterminer la
probabilité que ce composant fonctionne au moins 5 ans.
P(T >=5)=P(t>5) = 1- (1-exp(-5l)) = exp(-5l) = exp(-5x0,099)~0,61.
b.
On choisit au hasard un composant parmi ceux qui fonctionnent encore au
bout de 2 ans.
Déterminer la probabilité que ce composant ait une durée de vie
supérieure à 7 ans.
La loi exponentielle modèlise la durée de vie d'un phénomène sans
mémoire. Le fait que le phénomène ait duré pendant t heures ne change
rien à son espérance de vie à partir de l'instant t.
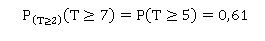
c. Donner
l’espérance mathématique E(T ) de la variable aléatoire T à l’unité
près.
Interpréter ce résultat.
E(T) = 1 / l = 1
/0,099 ~10,1 ans.
La durée de vie moyenne d'un composant est d'environ 10 ans.
|
| .
. |
|
|
Antilles Guyanne
Partie A.
Un fabricant d’ampoules possède deux machines, notées A et B. La
machine A fournit
65 % de la production, et la machine B fournit le reste. Certaines
ampoules présentent un défaut de fabrication :
- à la sortie de la machine A, 8 % des ampoules présentent un défaut ;
- à la sortie de la machine B, 5 % des ampoules présentent un défaut.
On définit les événements suivants :
- A : « l’ampoule provient de la machine A » ;
- B : « l’ampoule provient de la machine B » ;
- D : « l’ampoule présente un défaut ».
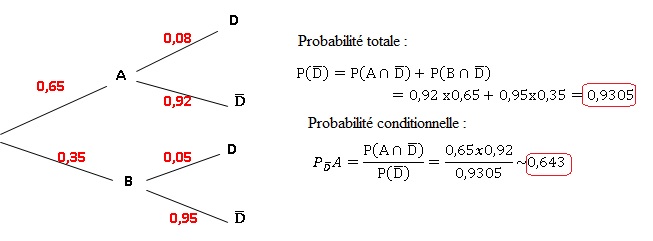
1. On prélève un
ampoule au hasard parmi la production totale d’une journée.
a. Construire un
arbre pondéré représentant la situation.
b. Montrer que la
probabilité de tirer une ampoule sans défaut est égale à 0,930 5.
c. L’ampoule tirée
est sans défaut. Calculer la probabilité qu’elle provienne de la
machine A.
2. On prélève 10
ampoules au hasard parmi la production d’une journée à la sortie de la
machine A. La taille du stock permet de considérer les épreuves comme
indépendantes et d’assimiler les tirages à tirages avec remise.
Calculer la probabilité d’obtenir au moins 9 ampoules sans défaut.
Loi Binomiale de paramètres n=10, p = 0,92
et q = 0,08.
au moins 9 ampoules
sans défaut signifie 9 ampoules ou 10 ampoules sans défaut.
A l'aide de la calculatrice p(X=9) +p(X=10) = 0,8121.
Partie B. Loi exponentielle.
a. Montrer que P(T
> a) = e−λa.
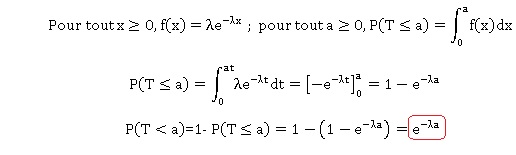
b. Montrer que si T
suit une loi exponentielle alors pour tous les réels positifs t et a on
a :
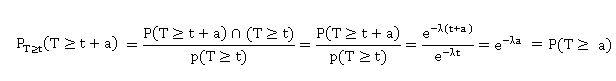
La
loi exponentielle modèlise la durée de vie d'un phénomène sans
mémoire. Le fait que le phénomène ait duré pendant t heures ne change
rien à son espérance de vie à partir de l'instant t.
2. Dans cette
partie, la durée de vie en heures d’une ampoule sans défaut est
une variable aléatoire T qui suit la loi exponentielle d’espérance 10
000.
a. Déterminer la
valeur exacte du paramètre l de
cette loi.
E(T) = 1 / l ; l = 1 / E(T) = 1 / 10000 =
0,0001.
b. Calculer la
probabilité P(T >5000).
P(T >5000) = exp(-5000l) =
exp(-5000x0,0001)=exp(-0,5) ~0,6065.
c.
Sachant qu’une ampoule sans défaut a déjà fonctionné pendant 7 000
heures, calculer la probabilité que sa durée de vie totale dépasse 12
000 heures.
D'après 1.b cette
probabilité est égale à
P(T >5000) ~0,6065.
Partie C.
L’entreprise a cherché à améliorer la qualité de sa production et
affirme qu’il n’y a pas plus de 6 % d’ampoules défectueuses dans sa
production. Une association de consommateurs réalise un test sur un
échantillon et obtient 71 ampoules défectueuses sur 1 000.
1. Dans le cas où
il y aurait exactement 6 % d’ampoules défectueuses, déterminer un
intervalle de fluctuation asymptotique au seuil de 95 % de la fréquence
d’ampoules défectueuses sur un échantillon aléatoire de taille 1 000.
Taille
de l'échantillon n = 1000, supérieur à 30.
Proportion de composants sans défaut p = 0,06 ; q = 1-p = 0,94.
np = 60, valeur supérieure à 5 ; nq = 940, valeur supérieure
à 5.
Les
conditions sont requises pour établir un intervalle de fluctuation
asymptotique au seuil de 95 % 1,96 (pq /n)½ = 1,96 (0,06
x0,94 /1000)½ =0,0147.
L'intervalle de fluctuation est : [ 0,06 -0,0147 ; 0,06 +0,0147) soit
[0,0453 ; 0,0747].
2. A-t-on des raisons de remettre en
cause l’affirmation de l’entreprise ?
71 /1000 =0 071.
Cette valeur appartient à l'intervalle de fluctuation. L'entreprise
n'est pas en cause.
|
|
|
|
Amérique
du sud.
Dans cet exercice, toutes les probabilités demandées seront arrondies à
10−4.
On étudie un modèle de climatiseur d’automobile composé d’un module
mécanique et d’un module électronique.
Si un module subit une panne, il est changé.
Partie A : Étude
des pannes du module mécanique.
Une enseigne d’entretien automobile a constaté, au moyen d’une étude
statistique, que la durée de fonctionnement (en mois) du module
mécanique peut être modélisée par une variable aléatoire D qui suit une
loi normale d’espérance μ = 50 et d’écart-type s :
1. Déterminer
l’arrondi à 10−4 de s
sachant que le service statistique indique que P(D >=48) = 0,7977.
P(D<48) = 1 -0,7977 = 0,2023.
On pose X = (D-µ) / s
; la variable aléatoire X suit la loi centrée réduite.
On cherche le nombre réel ß tel que P(X<ß) = 0,2023.
La calculatrice ou les tables donnent ß = - 0,833434.
(D-50) / s =
(48-50) / s = -2
/ s = -0,833434
; s = 2 /
0,833434 ~2,3997.
Pour la suite de cet exercice, on prendra s= 2,4.
2. Déterminer la
probabilité que la durée de fonctionnement du module mécanique soit
comprise entre 45 et 52 mois.
La calculatrice donne : P(D <45) = 0,01861 et P(D >52)=0,7977.
La probabilité que la durée de fonctionnement du module mécanique soit
comprise entre 45 et 52 mois vaut : 0,7977-0,01861 = 0,7791.
3. Déterminer la
probabilité que le module mécanique d’un climatiseur ayant fonctionné
depuis 48 mois fonctionne encore au moins 6 mois.
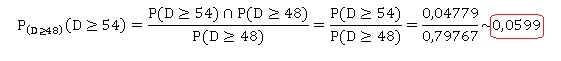
Partie B. Étude des pannes
d’origine électronique
Sur le même modèle de climatiseur, l’enseigne d’entretien automobile a
constaté que la durée de fonctionnement (en mois) du module
électronique peut être modélisée par une variable aléatoire T qui suit
une loi exponentielle de paramètre l.
1. Déterminer la
valeur exacte de l,
sachant que le service statistique indique que P(0<=T <=24) =
0,03.
P(0<=T <=24) = e0 -e-24l = 1-e-24l =0,03 ; e-24l =0,97 ; -24l = ln0,97 ; l = ln0,97 / 24 =0,00127.
Pour la suite de cet exercice, on prendra l = 0,00127.
2. Déterminer la
probabilité que la durée de fonctionnement du module électronique soit
comprise entre 24 et 48 mois.
e-24l -e-48l = e-24 x0,00127
-e -48 x0,00127=0,96997 -0,94086=0,0291.
3. a. Démontrer
que, pour tous réels t et a positifs, on a :
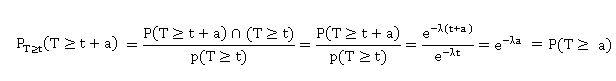
La
loi exponentielle modèlise la durée de vie d'un phénomène sans
mémoire. Le fait que le phénomène ait duré pendant t heures ne change
rien à son espérance de vie à partir de l'instant t.
b. Le module
électronique du climatiseur fonctionne depuis 36 mois. Déterminer la
probabilité qu’il fonctionne encore les 12 mois suivants.
P(T >12)= e-24l
=e -12 x0,00127=0,9849.
Partie C : Pannes
d’originemécanique et électronique
On admet que les évènements (D >48) et (T >48) sont indépendants.
Déterminer la probabilité que le climatiseur ne subisse aucune panne
avant 48 mois.
P(D >=48) x P(T >=48) = 0,79767 x e-48l =0,79767 x0,94086 = 0,7505.
Partie D : Cas
particulier d’un garage de l’enseigne
Un garage de l’enseigne a étudié les fiches d’entretien de 300
climatiseurs de plus de 4 ans. Il constate que 246 d’entre eux ont leur
module mécanique en état de fonctionnement depuis 4 ans.
Ce bilan doit-il remettre en cause le résultat donné par le service
statistique de l’enseigne, à savoir que P(D >48) = 0,7977 ?
Justifier la réponse.
n = 300 ; p =0,7977 ; 1-p = q = 0,2023 ;
n est supérieur à 30 ; np =300 x0,7977 ~ 239, valeur supérieure à 5 ;
nq = 300 x0,2023 ~60,7, valeur supérieure à 5.
Les conditions sont requises pour déterminer un intervalle de
fluctuation au seuil de 95 %.
1,96 ( p q / n)½= 1,96( 0,7977 x0,2023 / 300)½=0,04546.
Intervalle de fluctuation : [0,7977-0,04546 ; 0,7977 +0,04546] soit
[0,7522 ; 0,8432 ].
246 / 300 = 0,82 appartient à cet intervalle. Le bilan n'est pas remis
en cause.
|
|
Polynésie.
Partie A.
Un
astronome responsable d’un club d’astronomie a observé le ciel un soir
d’août 2015 pour voir des étoiles filantes. Il a effectué des relevés
du temps d’attente entre
deux apparitions d’étoiles filantes. Il a
alors modélisé ce temps d’attente, exprimé en minutes, par une variable
aléatoire T qui suit une loi exponentielle de paramètre l. En exploitant les données
obtenues, il a établi que l
= 0,2. Il prévoit d’emmener un groupe de nouveaux adhérents de son club
lors du mois d’août 2016 pour observer des étoiles filantes. Il suppose
qu’il sera dans des conditions d’observation analogues à celles d’août
2015. L’astronome veut s’assurer que le groupe ne s’ennuiera pas et
décide de faire quelques calculs de probabilités dont les résultats
serviront à animer la discussion.
1.
Lorsque le groupe voit une étoile filante, vérifier que la probabilité
qu’il attende moins de 3 minutes pour voir l’étoile filante suivante
est environ 0,451.
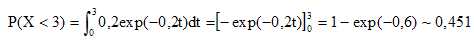
2.
Lorsque le groupe voit une étoile filante, quelle durée minimale
doit-il attendre pour voir la suivante avec une probabilité supérieure
à 0,95 ? Arrondir ce temps à la minute près.
On note T cette durée minimale. P(X<T) > 0,95 ; 1-exp(-0,2 T)
>0,95 ; exp(-0,2 T) < 0,05 ; -0,2 T < ln0,05
; T > - ln 0,05 /0,2 ; T > 15
minutes.
3.
L’astronome a prévu une sortie de deux heures. Estimer le nombre moyen
d’observations d’étoiles filantes lors de cette sortie.
Espérance de cette variable aléatoire E(T) = 1 / l = 1 /0,2 = 5 minutes.
En deux heures on peut espérer voir 120 / 5 = 24 étoiles filantes.
Partie B.
Ce responsable adresse un questionnaire à ses adhérents pour mieux les
connaître.
Il obtient les informations suivantes :
• 64% des personnes interrogées sont des nouveaux adhérents ;
• 27% des personnes interrogées sont des anciens adhérents qui
possèdent un télescope personnel ;
• 65% des nouveaux adhérents n’ont pas de télescope personnel.
1. On choisit un
adhérent au hasard. Montrer que la probabilité que cet adhérent possède
un télescope personnel est 0,494.
On
note les événements : T : l'adhérent interrogé possède un
télescope ; N : l'adhérent interrogé est un nouvel adhérent.
2.
On choisit au hasard un adhérent parmi ceux qui possèdent un télescope
personnel. Quelle est la probabilité que ce soit un nouvel adhérent ?
Arrondir à 10−3 près.
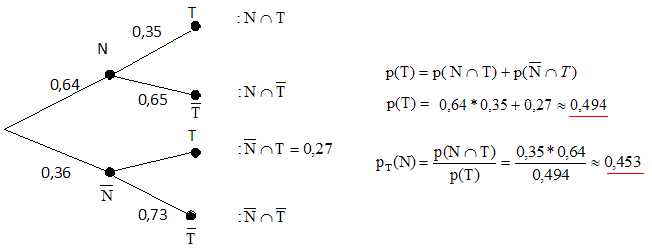
Partie C.
Pour
des raisons pratiques, l’astronome responsable du club souhaiterait
installer un site d’observation sur les hauteurs d’une petite ville de
2
500 habitants. Mais la pollution lumineuse due à l’éclairage public
nuit à la qualité des observations. Pour tenter de convaincre la mairie
de couper l’éclairage nocturne pendant les nuits d’observation,
l’astronome réalise un sondage aléatoire auprès de 100 habitants et
obtient 54 avis favorables à la coupure de l’éclairage nocturne.
L’astronome fait l’hypothèse que 50% de la population du village est
favorable à la
coupure de l’éclairage nocturne. Le résultat de ce sondage l’amène-t-il
à changer d’avis ?
Pour valider cette hypothèse on détermine
un intervalle de fluctuation au seuil de risque de 95 %.
p = 0,5 ; q=1-p=0,5 et n = 100.
n est
supérieur ou égal à 30 ; np = nq =50, valeurs supérieure à 5 : on peut
utiliser l'intervalle de fluctuation suivant :
(pq / n)½ =(0,5*0,5 / 100)½ =0,05 ; [0,5-0,05 ;
0,5 +0,05 ] soit [0,45 ; 0,55 ].
La valeur 0,54 appartient à cet intervalle, l'hypothèse est validée.
|
|