Mathématiques,
fonction, suite numérique, algorithme, Bac S 2016
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Centres
étrangers.
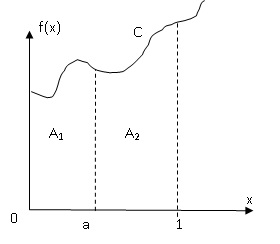
Soit
f une fonction définie sur l’intervalle [0 ; 1], continue et positive
sur cet
intervalle, et a une réel tel que 0< a < 1.
On note C la courbe représentative de la fonction f dans un repère
orthogonal, A1
l’aire du domaine plan limité par l’axe des abscisses et la courbe C
d’une part, les droites d’équations x = 0 et x = a d’autre part et A2
l’aire du domaine plan limité par l’axe des abscisses et la courbe C
d’une part, les droites d’équations x = a et x = 1 d’autre part.
Le but de cet exercice est de déterminer, pour différentes fonctions f
, une valeur du réel a vérifiant la condition (E) : « les aires A1
et A2 sont égales ».
On admet l’existence d’un tel réel a pour
chacune des fonctions considérées.
Partie A : Étude de
quelques exemples
1. Vérifier que
dans les cas suivants, la condition (E) est remplie pour un unique réel
a et déterminer sa valeur.
a. f est une
fonction constante strictement positive.
f(x )= k = constante.
A1 =a k ; A2
=(1-a) k ; ak = (1-a)k ; a = 1-a ; a = 0,5.
b.
f est définie sur [0 ; 1] par f (x) = x.
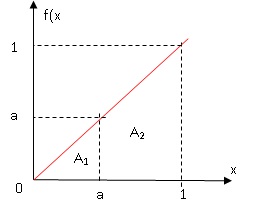
aire
du triangle A1 =a2/2 ; aire du trapèze A2 =(1+a)(1-a)
/2 =(1-a2) / 2 ; a2 = 1-a2 ; a = 2-½~0,707.
2. a.
À l’aide d’intégrales, exprimer, en unités d’aires, les aires A1
et A2.
b. On note F une
primitive de la fonction f sur l’intervalle [0 ; 1].Démontrer que si le
réel a satisfait la condition (E), alors F(a) =(F(0)+F(1))/2.
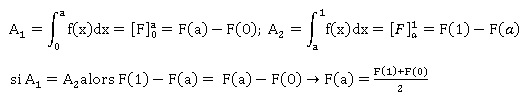
La
réciproque est-elle vraie ?
Soit F une primitive de f(x) telle que
F(a) = 0,5 F(0) +0,5 F(1).
A1 = F(a)-F(0) =0,5
F(0) +0,5 F(1)-F(0) =0,5 [F(1)-F(0)].
et A2=F(1)-F(a) =F(1)-0,5
F(0)-0,5F(1) = =0,5 [F(1)-F(0)].
La
condition A1 =A2
est vérifiée ; la réciproque est vraie.
3.
Dans cette question, on envisage deux autres fonctions particulières.
a. La fonction f
est définie pour tout réel x de [0 ; 1] par f (x) = ex .
Vérifier que la condition (E) est vérifiée
pour un unique réel a et donner sa valeur.
F
= ex ; A1
= F(a)-F(0) =ea-1 ; A2=F(1)-F(a) =e-ea.
A1 = A2=ea-1=e-ea ; ea
= (e+1)/2 ; a =[ ln(1+a) / 2].
b.
La fonction f définie pour tout réel x de [0 ; 1] par f (x) =1/(x +2)2
.
Vérifier que la valeur a =2/5 = 0,4 convient.
F = -1
/(2+x) ; F(a) = 0,5[ F(0) + F(1)] ; -1/(2+a)= 0,5 [-0,5-1/3)= -5 / 12 ;
5(2+a)=12 ; 10+5a=12 ; a = 2/5.
Partie B : Utilisation d’une suite
pour déterminer une valeur approchée de a.
Dans cette partie, on considère la fonction f définie pour tout réel x
de [0 ; 1] par
f (x) = 4−3x2.
1. Démontrer que si
a est un réel satisfaisant la condition (E), alors a est solution de
l’équation :
x =x3 /4 +3/8.
Primitive de f(x) : F = 4x-x3.
F(a)
= 0,5[ F(0) + F(1)] ; 4a-a3=0,5(0+4-1)
=3 /2 ; a =a3/4
+3/8.
Si a est un réel satisfaisant à la condition E, alors a est solution de
l'équation x =x3 /4 +3/8.
Dans
la suite , on admettra que cette équation a une unique solution dans
l’intervalle [0 ; 1]. On note a cette solution.
2. On considère la
fonction g définie pour tout réel x de [0 ; 1] par g (x)=x3
/4 +3/8 et la suite (un)
définie par : u0 = 0 et, pour tout entier naturel n, un+1
= g (un).
a. Calculer u1.
u1=g(u0)=g(0)=3/8.
b. Démontrer que la
fonction g est croissante sur l’intervalle [0 ; 1].
g est dérivable sur [0 ; 1] ; g'(x) = 0,75 x2.
g' est positive, donc g(x) est strictement croissante sur cet
intervalle.
c. Démontrer par
récurrence que, pour tout entier naturel n, on a :

d. Prouver que la
suite (un) est convergente. À l’aide des opérations sur les
limites, prouver que la limite est a.
La suite (un) est croissante et majorée par 1 : donc elle
converge.
un+1 = g(un) ; quand n tend vers l'infini, par
unicité des limites : la limite de un+1 est égale à la
limite de un, soit a.
g(un) = 0,25 un3
+3/8 ;
par produit et somme des limites, la limite de g(un)
est égale a 0,25 a3 +3/8.
e. On admet que le réel a vérifie
l’inégalité 0 < a−u10 < 10−9. Calculer u10
à10−8 près.
La calculatrice donne : u10 = 0,38980784.
|
| .
. |
|
|
Polynésie
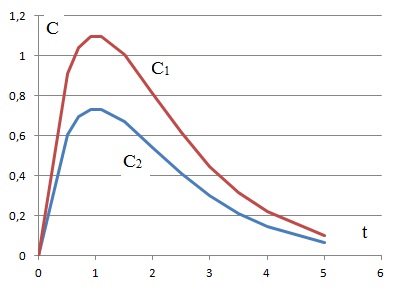
Voici deux courbes C1 et C2
qui donnent pour deux personnes P1 et P2
de corpulences différentes la concentration C d’alcool dans le sang
(taux d’alcoolémie) enfonction du temps t après ingestion de la même
quantité d’alcool. L’instant t = 0correspond aumoment où les deux
individus ingèrent l’alcool. C est exprimée en gramme par litre et t en
heure.
Définition : La corpulence est le nom scientifique correspondant au
volume du corps.
Partie A.
1.
La fonction C est définie sur l’intervalle [0 ; +oo[ et on note C′ sa
fonction dérivée. À un instant t positif ou nul, la vitesse
d’apparition d’alcool dans le sang est donnée par C′(t ).
À quel instant cette vitesse est-elle maximale ?
La vitesse d'apparition de l'alcool dans le sang est maximale à
l'instant t =0; à cet instant le coefficient directeur de la tangente à
la courbe est le plus grand.
On dit souvent qu’une personne de faible corpulence subit plus vite les
effets de l’alcool.
2. Sur le graphique
précédent, identifier la courbe correspondant à la personne la plus
corpulente. Justifier le choix effectué.
A la plus grande vitesse d'apparition de l'alcool dans le sang ( courbe
C1 ), au maximum le plus élevé, correspond la personne
de faible corpulence.
3. Une personne à
jeun absorbe de l’alcool. On admet que la concentration C d’alcool dans
son sang peut être modélisée par la fonction f définie sur [0 ; +oo[
par f (t )= Ate−t où A est une constante positive qui
dépend de la corpulence et de la quantité d’alcool absorbée.
a. On note f ′ la
fonction dérivée de la fonction f . Déterminer f ′(0).
On pose u =A t et v = e-t ; u' = A et v' = -e-t ;
f '(x) =u'v+v'u= Ae-t -Ate-t = Ae-t(1-t).
f '(0) = A.
b. L’affirmation
suivante est-elle vraie ?
« À quantité d’alcool absorbée égale, plus A est grand, plus la
personne est corpulente. »
L'affirmation est fausse. La plus grande valeur de A correspond la plus
grande vitesse d'apparition d'alcool dans le sang, c'est à dire à la
personne la moins corpulente.
Partie B. Un
cas particulier
Paul, étudiant de 19 ans de corpulence moyenne et jeune conducteur,
boit deux verres de rhum. La concentration C d’alcool dans son sang est
modélisée en fonctiondu temps t , exprimé en heure, par la fonction f
définie sur [0 ; +oo[ par f (t ) = 2te−t .
1. Étudier les
variations de la fonction f sur l’intervalle [0 ; +oo[.
f '(x) = 2e-t(1-t).
f '(x) s'annule pour t = 1 ; f '(x) est positive pour t inférieur à une
heure et négative pour t > 1.
f(x) est croissante sur [0 ; 1 [, décroissante sur ]1 ; +oo[ et passe
par un maximum pour t =1.
2. À quel instant la concentration
d’alcool dans le sang de Paul est-elle maximale ? Quelle est alors sa
valeur ? Arrondir à 10−2 près.
f(1) = 2 e-1 = 2 / e ~0,74 g / L.
3. Rappeler la
limite de et / t lorsque t tend vers +oo et en déduire celle
de f (t ) en +oo.
Interpréter le résultat dans le contexte de l’exercice.
Par croissance comparée la limite de et / t est l'infini
lorsque t tend vers l'infini.
A l'inverse la limite de t / et est égale à zéro lorsque t
tend vers l'infini.
f(t) tend vers zéro au bout d'u temps très long. L'alcool est éliminé
du sang au bout d'un temps suffisamment grand.
4. Paul veut savoir
au bout de combien de temps il peut prendre sa voiture.
On rappelle que la législation autorise une concentration maximale
d’alcool dans le sang de 0,2 g.L−1 pour un jeune conducteur.
a. Démontrer qu’il
existe deux nombres réels t1 et t2 tels que f (t1)
= f (t2) = 0,2.
f
est continue et croissante sur [0 ; 1 ] et prend des valeurs comprises
entre 0 et 2 /e.
De plus 0,2 appartient à [0 ; 2 / e], d'après le théorème des valeurs
intermédiaires, l'équation f(t) = 0,2 admet une solution unique sur cet
intervalle.
f est continue et décroissante sur [1 ;
+oo ] et prend des valeurs comprises entre 0 et 2 /e.
De plus 0,2 appartient à [0 ; 2 / e], d'après le théorème des valeurs
intermédiaires, l'équation f(t) = 0,2 admet une solution unique sur cet
intervalle.
b. Quelle durée minimale Paul
doit-il attendre avant de pouvoir prendre le volant en toute légalité ?
Donner
le résultat arrondi à la minute la plus proche.
f(3,5) = 0,211 ; f(3,58) =0,199 g/L.
3,58 h = 3 h 35 min.
5. La concentration
minimale d’alcool détectable dans le sang est estimée à 5×10−3
g.L−1.
a. Justifier qu’il
existe un instant T à partir duquel la concentration d’alcool dans le
sang n’est plus détectable.
On pose e =
5 x 10-3. Par définition de la limite, il existe un nombre
réel T, tel que pour tout t > T, f(t) appartient à l'intervalle ] -e ; +e [.
b. On donne
l’algorithme suivant où f est la fonction définie par f (t ) = 2te−t
.
Initialisation : t prend la valeur 3,5
p prend la valeur 0,25
C prend la valeur 0,21
Traitement : Tant que C > 5×10−3 faire :
t prend la valeur t +p
C prend la valeur f (t )
Fin Tant que
Sortie : Afficher t
Recopier et compléter le tableau de valeurs suivant en exécutant cet
algorithme. Arrondir les valeurs à 10−2 près.
|
Initialisation
|
Etape
1
|
Etape
2
|
p
|
0,25
|
0,25
|
0,25
|
t
|
3,5
|
3,75
|
4,00
|
C
|
0,21
|
0,18
|
0,15
|
Cet algorithme affiche le temps en heures,
au bout duquel l'alcool n'est plus détectable dans le sang.
Suite numérique.
Soit u la suite définie par u0 = 2 et, pour tout entier
naturel n, par un+1 = 2un +2n2 −n.
On considère également la suite v définie, pour tout entier naturel n,
par vn = un +2n2 +3n +5.
Voici un extrait de feuille de tableur :
|
A
|
B
|
C
|
1
|
n
|
u
|
v
|
2
|
0
|
2
|
7
|
3
|
1
|
4
|
14
|
4
|
2
|
9
|
28
|
5
|
3
|
24
|
56
|
6
|
4
|
63
|
|
Quelles formules a-t-on écrites dans les cellules C2 et B3 et copiées
vers le bas pour afficher les termes des suites u et v ?
Cellule C2 : = B2+2*A2*A2+3*A2+5
Cellule B3 : = 2*B2+2*A2*A2-A2
2. Déterminer, en
justifiant, une expression de vn et de un en fonction de n
uniquement.
D'après le tableau : vn= 7 x2n.
Démonstration
par récurrence :
Initialisation
: pour n = 0, u0 = 2, v0 = 7 x20=7,
propriété vraie au rang 0.
Hérédité :
soit p un entier naturel : up
= 7x2p
-2p2 −3p-5.
Par suite up+1=2up
+2p2 −p=2(7x2p -2p2 −3p-5)+2p2 −p ;
up+1=7x2p+1
-4p2
−6p-10+2p2 −p ;
up+1=7x2p+1
-2p2
−7p-10=7x2p+1
-2[(p+1)2-2p-1]
−7p-10 ;
up+1=7x2p+1
-2(p+1)2-3p-8
;
up+1=7x2p+1
-2(p+1)2-3(p+1-1)-8
;
up+1=7x2p+1
-2(p+1)2-3(p+1)+5.
La propriété est donc héréditaire.
Conclusion
: quel que soit n entier naturel, un = 7x2n -2n2
−3n-5 et vn=
7 x2n.
|
|
|
|
Métropole.
Soit f la fonction définie sur R par f (x) = x −ln(x2 +1)
1. Résoudre dans R l’équation : f (x) = x.
x = x-ln(1+x2) ; ln(1+x2) = 0 = ln 1 ; x2
= 0 ; x = 0.
2. Justifier tous
les éléments du tableau de variations ci-dessous à l’exception de la
limite de la fonction f en +oo que l’on admet.
f ' (x) = 1 -2x / (1+x2) = (1+x2-2x) / (1+x2)
= (1-x)2 / (1+x2).
La dérivée s'annule pour x = 1 ; f '(x) est positive sur R : f(x) est
strictement croisssante sur R..
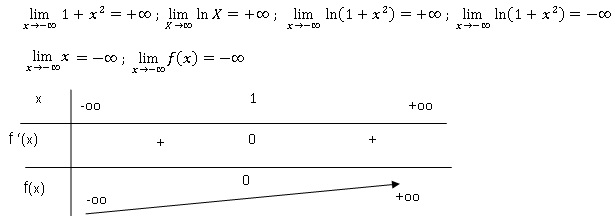
3. Montrer que,
pour tout réel x appartenant à [0 ; 1], f (x) appartient à [0 ; 1].
f(0) = 0 ; f(1) = 1-ln2 <1.
De plus la fonction est strictement croissante : donc pour tout réel x
appartenant à [0 ; 1], f (x) appartient à [0 ; 1].
4. On considère
l’algorithme suivant :
Variables N et A des entiers naturels ;
Entrée Saisir la valeur de A
Traitement N prend la valeur 0
Tant que N −ln(N2 +1)< A
N prend la valeur N +1
Fin tant que
Sortie Afficher N
a. Que fait cet
algorithme ?
Il affiche la plus petite valeur de N pour laquelle N −ln(N2
+1) est supérieur ou égal à A.
b. Déterminer la
valeur N fournie par l’algorithme lorsque la valeur saisie pour A est
100.
L'algorithme affiche 110 pour A = 100.
Partie B.
Soit (un) la suite définie par u0 = 1 et, pour
tout entier naturel n, un+1 = un−ln(u2n+1)
1. Montrer par
récurrence que, pour tout entier naturel n, un appartient à
[0 ; 1].
Initialisation
: u0=1, la propriété est vraie au rang 0.
Hérédité :
supposons la propriété vraie pour un.
Si un appartient à [0 ; 1], alorsd'après la question
3, f(un) appartient à [0 ; 1].
Or f(un) = un+1 ; donc un+1 appartient
à [0 ; 1]. La propriété est donc héréditaire.
Conclusion
: la propriété est vraie au rang 0 et héréditaire, donc pour tout
entier naturel n, un appartient à [0 ; 1].
2. Étudier les
variations de la suite (un).
un+1 - un = −ln(u2n+1).
La fonction carrée est croissante sur [0 ; 1] ; un
appartient à [0 ; 1), donc u2n appartient à [0 ;
1 ].
En conséquence 1 + u2n appartient à [1 ; 2 ].
De plus la fonction logarithme est croissante , donc ln(1 + u2n
) est supérieure ou égale à ln1.
ln(1 + u2n ) est positif ou nul ; -ln(1 + u2n
) est négatif.
un+1 - un est négatif : la suite est décroissante.
3. Montrer que la
suite (un) est convergente.
La suite est décroissante et minorée par zéro, elle converge donc vers
une limite..
4. On note ℓ sa limite, et on admet que ℓ vérifie l’égalité f (ℓ)= ℓ.
En déduire la valeur de ℓ.
L'équation f(x) = x admet une solution unique x=0 ; donc ℓ = 0.
|
|
Asie
Une
société produit des bactéries pour l’industrie. En laboratoire, il a
été mesuré que, dans un milieu nutritif approprié, la masse de ces
bactéries, mesurée en grammes,
augmente de 20% en un jour. La société met en place le dispositif
industriel suivant.
Dans une cuve de milieu nutritif, on introduit initialement 1 kg de
bactéries. Ensuite, chaque jour, à heure fixe, on remplace le milieu
nutritif contenu dans la cuve. Durant
cette opération, 100 g de bactéries sont perdus. L’entreprise se fixe
pour objectif de produire 30 kg de bactéries.
Partie A : premie
rmodèle – avec une suite
On modélise l’évolution de la population de bactéries dans la cuve par
la suite (un) définie de la façon suivante :
u0 = 1000 et, pour tout entier naturel n, un+1 =
1,2un −100.
1. a. Expliquer en
quoi ce modèle correspond à la situation de l’énoncé. On précisera en
particulier ce que représente un.
un représente la masse des bactéries contenues dans la
cuve le jour n.
La masse des bactéries croît d'un facteur 1,2 chaque jour et 100 g de
bactéries sont perdues chaque jour en changeant de milieu nutritif.
b. L’entreprise
souhaite savoir au bout de combien de jours la masse de bactéries
dépassera 30 kg. À l’aide de la calculatrice, donner la réponse à ce
problème.
Chercher le plus petit entier n tel que un > 30 000.
u22 ~28100 ; u23 ~ 33600. On retient n = 23 jours.
c. On peut
également utiliser l’algorithme suivant pour répondre au problème posé
dans la question précédente.
Recopier et compléter cet algorithme.
Variables u et n sont des nombres
u prend la valeur 1 000
n prend la valeur 0
Traitement Tant que u < 30000
faire
u prend la valeur 1,2 u-100
n prend la valeur n +1
Fin Tant que
Sortie Afficher n
2. a. Démontrer par
récurrence que, pour tout entier naturel n, un est supérieur
ou égal à 1000.
Initialisation
: u0 = 1000, la propriété est vraie au rang 0.
Hérédité :
supposons la propriété vraie pur un.
un+1 = 1,2 un -100 ; un supérieur ou
égal à 1000, donc 1,2 un est supérieur ou égal à 1200 et 1,2
un -100 est supérieur ou égal à 1100.
1,2 un -100 est supérieur ou égal à 1000. La propriété est
vraie au rang n+1. La propriété est héréditaire.
Conclusion
: la propriété est vraie au rang 0 et héréditaire, donc pour tout
entier naturel n, un est supérieur ou égal à 1000.
b. Démontrer que la
suite (un) est croissante.
un+1 -un= 0,2 un -100 ;
un supérieur ou égal à 1000, donc 0,2 un est
supérieur ou égal à 200 et 0,2 un -100 est supérieur ou égal
à 100.
un+1 -un est positif, la suite est donc
croissante.
3. On définit la
suite (vn) par : pour tout entier naturel n, vn =
un −500.
a. Démontrer que la
suite (vn) est une suite géométrique.
v0 = u0 −500 = 1000-500 = 500.
un+1=1,2 un-100 ; vn+1 = un+1
−500 =1,2 un-100-500= 1,2(un-500)= 1,2 vn.
Il s'agit d'une suite géomètrique de premier terme 500 et de raison q =
1,2.
b. Exprimer vn,
puis un, en fonction de n.
vn=500 x1,2n.
c. Déterminer la
limite de la suite (un).
Le premier terme est positif et la raison est supérieure à 1. La suite
tend vers l'infini quand n tend vers l'infini.
Partie B. second modèle – avec une
fonction.
On constate qu’en pratique, la masse de bactéries dans la cuve ne
dépassera jamais 50 kg. Cela conduit à étudier un second modèle dans
lequel la masse de bactéries
est modélisée par la fonction f définie sur 0 ; +oo par : f (t )=50 /
[1+49exp(−0,2t)]
où t représente le temps exprimé en jours et où f (t ) représente la
masse, exprimée en kg, de bactéries au temps t .
1. a. Calculer f
(0).
f(0)=50 / (1+49)=1.
b. Démontrer que,
pour tout réel t0, f (t ) < 50.
exp(−0,2t) est positif ; 1+49exp(−0,2t)
est supérieur à1 ; son inverse 1 /
[1+49exp(−0,2t)] est inférieur à1.
par suite f(t) est inférieur à 50.
c. Étudier le sens de variation
de la fonction f .
On pose u = 1+49exp(−0,2t) ; u' = -0,2 x49exp(−0,2t)
= -9,8exp(−0,2t)
f '(t) = 50(-u'/u2) = 490exp(−0,2t)
/ [1+49exp(−0,2t)]2.
La dérivée étant toujours positive, la fonction f(t) est strictement
croissante sur [0 ; +oo[.
d. Déterminer
la limite de la fonction f en +oo.
Si t tend vers l'infini : exp(−0,2t)
tend vers zéro ; 49exp(−0,2t) tend vers
zéro ; 1+49exp(−0,2t) tend vers 1 ; f(t) tend
vers 50.
2.
Interpréter les résultats de la question 1 par rapport au contexte.
f(t) correspond à la masse de bactéries.
La masse initiale de bactéries est égale à 1 kg.
La masse de bactéries est croissante au cours du temps tout en restant
inférieure à 50 kg.
Au bout d'un temps suffisamment long, la masse des bactéries se
rapproche de 50 kg.
3. En utilisant ce
modèle, on cherche à savoir au bout de combien de jours la masse de
bactéries dépassera 30 kg.
Résoudre l’inéquation d’inconnue t : f (t )> 30. En déduire la
réponse au problème.
50 / [1+49exp(−0,2t)] > 30 ; 1+49exp(−0,2t)<
5 /3 ; 49exp(−0,2t)< 2 /3 ; exp(−0,2t)
< 2 / (3x49).
-0,2t < ln(2/ (3x49)) ; t >5 ln(3 x49 / 2) ; t > 21,5 jours.
Au bout de 22 jours, la masse des bactéries dépasse 30 kg.
Partie C. Un
contrôle de qualité
Les bactéries peuvent être de deux types : le type A, qui produit
effectivement une protéine utile à l’industrie, et le type B, qui ne la
produit pas et qui est donc inutile
d’un point de vue commercial. L’entreprise affirme que 80% des
bactéries produites sont de type A.
Pour vérifier cette affirmation, un laboratoire analyse un échantillon
aléatoire de 200 bactéries en fin de production. L’analyse montre que
146 d’entre elles sont de type A.
L’affirmation de l’entreprise doit-elle être remise en cause ?
Taille de l'échantillon n = 200.
Proportion de bactéries utiles p = 0,80 ; q = 1-p = 0,20.
n >50 ; np = 160, valeur supérieure à 5 ; nq = 40, valeur supérieure
à 5.
Les conditions sont requises pour établir un intervalle de fluctuation
au seuil de 95 %.
1,96 (pq/n)½ = 1,96 (0,8 x0,2 / 200)½ =0,055.
Intervalle de fluctuation [0,8 -0,055 ; 0,8 +0,055 ] soit [0,74 ; 0,86]
146 / 200=0,73, cette valeur n'appartient pas à l'intervalle de
fluctuation. L'affirmation de l'entreprise doit être remise en cause,
au risque de 5 %.
|
|