Mathématiques,
Fonction logaritme, exponentielle, Bac S 2016
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Pondichéry.
Soit
f la fonction définie sur ]0 ; 14] par f (x) = 2−ln(x/2)
La courbe représentative Cf de la fonction f est donnée dans
le repère orthogonal d’origine O ci-dessous :
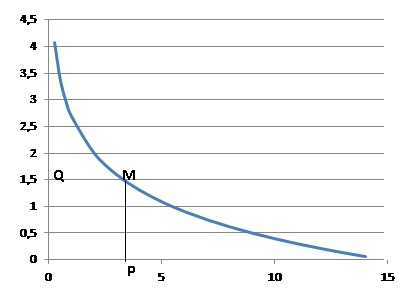
À tout point M appartenant à Cf on associe le
point P projeté orthogonal de M sur l’axe des abscisses, et le point Q
projeté orthogonal de M sur l’axe des ordonnées.
1. L’aire du
rectangle OPMQ est-elle constante quelle que soit la position du point
M sur Cf ?
Aire du rectangle Y = OP x MP = x(2-ln(x/2).
Cette aire n'est pas constante. Elle dépend de la position du point M.
2.
L’aire du rectangle OPMQ peut-elle être maximale ? Si oui, préciser les
coordonnées du point M correspondant. Justifier les réponses.
Dériver Y : on pose u = x et v = 2
-ln(0,5 x) = 2 -ln0,5 - ln x
u' = 1 ; v' = -1/x.
Y' = u'v + v'u = 2-ln(0,5x) -1 = 1-ln(0,5x).
Y' s'annule pour ln(0,5 x) = 1 ; 0,5 x = e ; x = 2e.
Y' est positive pour x < 2e et négative pour
x > 2e3.
Y est croissante pour x < 2e et décroissantee
pour x > 2e.
L'aire est maximale pour x =2e
et vaut Ymax =2e(2-ln(e)) =2e.
Coordonnées du point M : x = 2e ; y = 2-ln(e) = 1.
On souhaite stériliser une
boîte de conserve.
Pour cela, on la prend à la température ambiante T0 = 25 °C
et on la place dans un four à température constante TF = 100
°C. La stérilisation débute dès lors que la température de la boîte est
supérieure à 85 °C.
Partie A :
Modélisation discrète.
Pour n entier naturel, on note Tn la température en degré
Celsius de la boîte au bout de n minutes. On a donc T0 = 25.
Pour n non nul, la valeur Tn est calculée puis affichée par
l’algorithme suivant :
Initialisation : T prend la valeur 25
Traitement : Demander la valeur de n
Pour i allant de 1 à n faire
T prend la valeur 0,85×T +15
Fin Pour
Sortie : Afficher T
1. Déterminer la
température de la boîte de conserve au bout de 3 minutes. Arrondir à
l’unité.
T1 = 0,85 x 25+15 =36,25° ; T2 = 0,85 x
36,25 +15~45,8° ; T3 = 0,85 x45,8 +15 ~53,9°.
2. Démontrer que,
pour tout entier naturel n, on a Tn = 100−75×0,85n.
T0 =100-75 = 25. Cette propriété est vraie pour n=0.
On suppose que cette propriété est vrai au rang p ( positif ou nul) : Tp = 100−75×0,85p.
Tp+1 = 0,85 Tp +15 = 0,85 x(100−75×0,85p) +15.
Tp+1 = 85-75×0,85p+1
+15 = 100-75×0,85p+1
; cette propriété est vrai au rang p+1.
Cette propriété est vrai au rang zéro et elle est héréditaire pour tout
p positif ou nul, elle est donc vraie pour tout n positif ou nul.
3. Au bout de combien deminutes la
stérilisation débute-elle ?
85 = 100−75×0,85n ; 75×0,85n =
15 ; 0,85n =0,2
; n log0,85 = log 0,2 ; n = 9,9 ~ 10 minutes.
Partie B : Modélisation continue
Dans cette partie, t désigne un réel positif.
On suppose désormais qu’à l’instant t (exprimé en minutes), la
température de la boîte est donnée par f (t ) (exprimée en degré
Celsius) avec : f (t )= 100−75exp(−ln5/10 t ).
1. a. Étudier le
sens de variation de f sur [0 ; +∞[.
Dériver : f '(t) = -75 x(-ln5 /10) exp(−ln5/10 t ).
f '(t) = 7,5 ln 5 exp(−ln5/10 t ) positive
quelque soit t.
f est strictement croissante sur [0 ; +∞[.
b. Justifier que si t >10 alors
f (t )>85.
f(10) = 100-75 exp(-ln5) = 100-75 exp (ln0,2)=100-75 x0,2 = 85.
De plus f est strictement croissante sur cet intervalle. Donc pour t
>10, f est supérieure à 85 °.
2. Soit q un réel supérieur ou égal
à 10.
On note A(q) le
domaine délimité par les droites d’équation t = 10, t = q, y = 85 et la courbe
représentative Cf de f . On considère que la stérilisation
est finie au bout d’un temps q,
si l’aire, exprimée en unité d’aire du domaine A(q) est supérieure à 80.
a. Justifier,
à l’aide du graphique donné, que l’on a A(25) > 80.
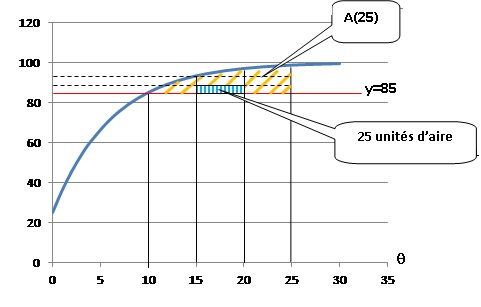
A(25) est hachurée en jaune. le petit rectangle hachuré en bleu
correspond à 25 unités d'aire.
A(25) contient au moins 4 petits rectangles bleus, soit plus de 80
unités d'aire.
b. Justifier que, pour θ supérieur
ou égal à 10 on a :
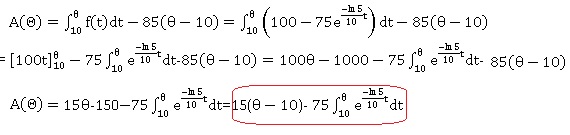
c. La stérilisation
est-elle finie au bout de 20 minutes ?
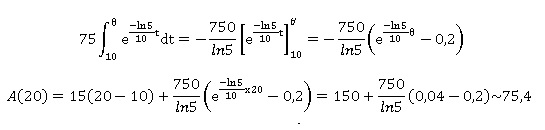
A(20) étant inférieure à 80, la stérélisation n'est pas terminée au
bout de 20 minutes.
|
| .
. |
|
|
Liban.
On considère la fonction f définie sur l’intervalle
[0 ; 1] par : f (x) =1 / [1+exp(1-x)].
Partie A.
1. Étudier le sens
de variation de la fonction f sur l’intervalle [0 ; 1].
On pose u = 1-x ; u' = -1. On pose v = 1+exp(1-x) ; v' = -exp(1-x).
Dériver : f '(x) = -v' / v2 = exp(1-x)/ [1-exp(1-x)]2.
Sur l'intervalle
[0 ; 1], f '(x) est positive ; f(x) est strictement croissante sur cet
intervalle.
2.
Démontrer que pour tout réel x de l’intervalle [0 ; 1], f (x) =ex/
(ex +e)
On multiplie numérateur et dénominateur par ex.
f(x) =ex/ [ ex+ex.e(1-x)]=ex/
[ ex+e(1-x+x)]=ex/ (ex +e).
3.
Montrer alors que :
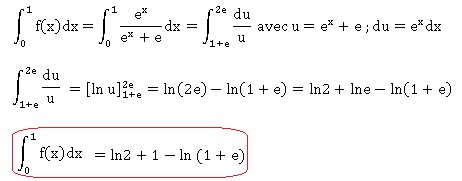
Partie B.
Soit n un entier naturel. On considère les fonctions fn
définies sur [0 ; 1] par :
fn(x) = 1 / [1+n e1−x ].
On note Cn la courbe représentative de la fonction fn
dans le plan muni d’un repère orthonormé.
On considère la suite de terme général 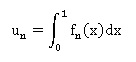
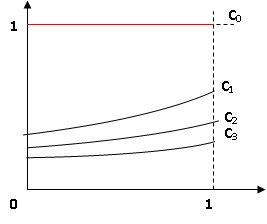
1. On a tracé les
courbes représentatives des fonctions fn pour n variant de 1
à 3. Compléter le graphique en traçant la courbe C0
représentative de la fonction f0.
2. Soit n un entier
naturel, interpréter graphiquement un et préciser la valeur
de u0.
Un représente l'aire comprise entre la courbe, l'axe des
abscisses et les droites d'équation x=0 et x = 1 avec u0 = 1.
3. Quelle
conjecture peut-on émettre quant au sens de variation de la suite (un)
? Démontrer cette conjecture.
Les aires sont de plus en plus petites. La suite est décroissante.
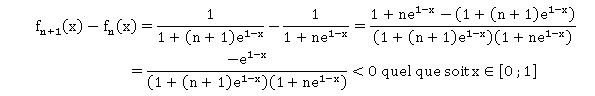
De plus l'intégration sur un intervalle conserve l'ordre. La suite un
est strictement décroissante.
4. La suite (un) admet-elle une limite ?
Pour tout entier naturel de l'intervalle [0 ; 1 ] :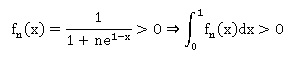
La suite est décroissante et minorée par zéro, elle converge et admet
une limite finie.
|
|
|
|
Amérique
du Nord.
Un
particulier veut faire fabriquer un récupérateur d’eau. Ce récupérateur
d’eau est une cuve qui doit respecter le cahier des charges suivant
elle doit être située à deux mètres de sa maison ; la profondeur
maximale doit être de deux mètres ; elle doit mesurer cinq mètres de
long ;
elle doit épouser la pente naturelle du terrain.
La partie incurvée est modélisée par la courbe Cf de la fonction f sur
l’intervalle [2 ; 2e] définie par :
f (x) = x ln( x/2)−x +2.
La courbe Cf est représentée ci-dessous dans un repère
orthonormé d’unité 1 m et constitue une vue de profil de la cuve.
On considère les points A(2 ; 2), I(2 ; 0) et B(2e ; 2).
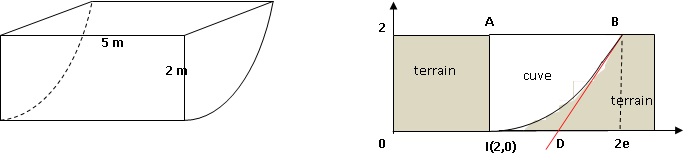
L’objectif de cette partie est d’évaluer le volume de la cuve.
1. Justifier que
les points B et I appartiennent à la courbe Cf et que l’axe
des abscisses est tangent à la courbe Cf au point I.
f(xB)=f(2e) = 2e ln (e)-2e+2=2= yB ; f(xI)=f(2)
=2 ln (1)-2+2=0 = yI.
f '(x) = ln(x/2) +1 -1=ln(x/2) ; coefficient directeur de la tangente à
Cf en I : f '(2) = 0.
La tangente à la courbe est horizontale en I.
2. On note T la
tangente à la courbe Cf au point B, et D le point
d’intersection de la droite T avec l’axe des abscisses.
a. Déterminer une
équation de la droiteT et en déduire les coordonnées de D.
Coefficient directeur de la droite T : f '(2e) = ln(e) = 1.
Equation de cette droite y = x+b avec b une constante.
T passe en B(2e ; 2) : 2 = 2e +b d'où b = 2-2e.
Equation de T : y = x +2-2e.
Coordonnée du point D ( 2e-2 ; 0).
b. On appelle S
l’aire du domaine délimité par la courbeCf , les droites
d’équations y = 2, x = 2 et x = 2e.
S peut être encadrée par l’aire du triangle ABI et celle du trapèze
AIDB. Quel encadrement du volume de la cuve peut-on en déduire ?
Aire du triangle AIB : AI . AB / 2 = 2 x (2e-2) / 2 = 2e-2.
Aire du trapèze ABDI : (AB + ID) . AI / 2 = (2e-2 +2e-4) x 2 / 2 = 4e-6.
Le volume de la cuve est compris entre (2e-2) x5 = 10(e-1) m3
et (4e-6) x5 = 10(2e-3) m3.
3. a. Montrer que,
sur l’intervalle [2 ; 2e], la fonction G définie par
G(x) =0,5 x2 ln (0,5x) -0,25 x2
est une primitive de la fonction g définie par g (x) = x ln(0,5x).
Dériver G(x) ; on pose u = 0,5 x2 et v = ln(0,5x) ; u' = x
et v' = 1/x.
u'v +v'u = x ln(0,5x) +0,5x
G'(x) = x ln(0,5x) +0,5x-0,5 x = x ln(0,5x) = g(x).
b. En déduire une
primitive F de la fonction f sur l’intervalle [2 ; 2e].
F(x) = G(x) -0,5 x2 +2x = 0,5 x2 ln (0,5x) -0,75 x2
+2x.
c. Déterminer la
valeur exacte de l’aire S et en déduire une valeur approchée du volume
V de la cuve au m3 près.
Aire S =2(2e-2)-[ F(2e) -F(2)] =4e-4-[0,5 (2e)2ln(e)-0,75(2e)2
+4e-(2ln(1)-3+4)]= e2 -3.
V =5(e2-3)~22 m3.
Pour tout réel x compris entre 2 et 2e, on note v(x) le volume d’eau,
exprimé en m3, se trouvant dans la cuve lorsque la hauteur
d’eau dans la cuve est égale à f (x). On admet que, pour tout réel x de
l’intervalle [2 ; 2e],
v(x) = 5[0,5x2ln(0,5x) -2xln(0,5x)-0,25x2+2x-3]
1. Quel volume
d’eau, au m3 près, y a-t-il dans la cuve lorsque la hauteur
d’eau dans la cuve est de un mètre ?
f(x) = 1 ; x ln( x/2)−x +2 = 1 ; x ln( x/2)−x +1 =0 ;
f(3) = 0,216 ; f(4) = 0,773 ; f(4,5)=1,15 ; f(4,4) =1,07 ; f(4,3)=0,99.
v(4,3)=5[0,5*4,32 ln(2,15)-8,6ln(2,15)-0,25*4,32+8,6-3]~7,4
~7 m3.
On considère l’algorithme suivant :
Variables : a est un réel
b est un réel
Traitement : a prend la valeur 2
b prend la valeur 2 e
Tant que v(b) − v(a) > 10−3
faire :
c prend la valeur (a +b)/2
Si v(c) <V /2, alors :
a prend la valeur c
Sinon
b prend la valeur c
Fin Si
Fin Tant que
Sortie : Afficher f (c)
Interpréter le résultat que cet algorithme permet d’afficher.
Cet algorithme affiche la hauteur d'eau correspondant au rempissage
égal à la moitié de la capacité totale.
|
|
Antilles Guyanne.
Partie A.
On considère la fonction f définie pour tout réel x par f (x) = x
exp(1−x2)..
1. Calculer la
limite de la fonction f en +oo.
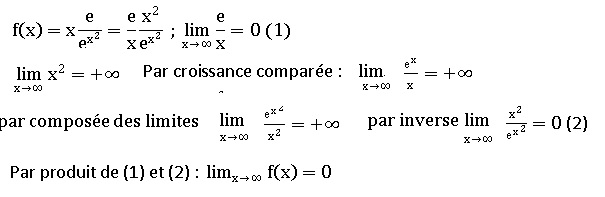
On admettra que la limite de la fonction f en −∞est égale à 0.
2. a. On admet que
f est dérivable sur R et on note f ′ sa dérivée.
Démontrer que pour tout réel x, f ′(x) =(1-2x2) exp(1-x2).
On pose w = 1-x2 ; .u = x ; v = ew ; w' = -2x ;
u' = 1 ; v' = -2x exp(1-x2).
Dérivée d'un produit : u'v +v'u = exp(1-x2) -2x2
exp(1-x2) =(1-2x2) exp(1-x2).
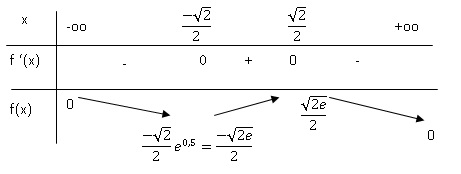
b. En déduire le
tableau de variations de la fonction f .
exp(1-x2) est toujours positif. f '(x) a le signe de (1-2x2).
f '(x) s'annule pour x = ±2-½. f '(x) est positive pour x
appartenant à ]-2-½ ; +2-½ [.
Partie B.
On considère la fonction g définie pour tout réel x par g (x) = e1−x
.
Sur le graphique ci-dessous, on a tracé dans un repère les courbes
représentatives Cf et Cg respectivement des
fonctions f et g.
Le
but de cette partie est d’étudier la position relative de ces deux
courbes.
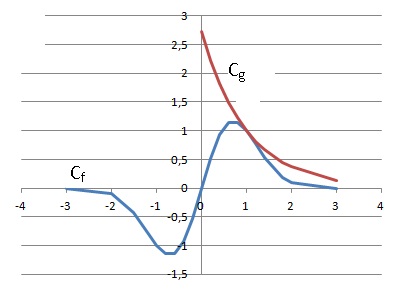
1. Après
observation du graphique, quelle conjecture peut-on émettre ?
Il apparaît que Cg est toujours au dessus de Cf.
2. Justifier que,
pour tout réel x appartenant à ]−oo; 0], f (x) < g (x).
Quel que soit x négatif ou nul exp(1-x) est positif alors que (1-x2)
exp(1-x2) est négatif. Donc f
(x) < g (x) et Cg
est au dessus de Cf.
3.
Dans cette question, on se place dans l’intervalle ]0 ; +∞[.
On pose, pour tout réel x strictement positif, F(x)= lnx −x2 +x.
a. Montrer que,
pour tout réel x strictement positif, f (x) inférieur ou égal à g
(x) équivaut à F(x) inférieur ou égal à zéro.
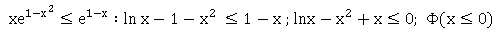
On admet pour la suite que f (x) = g (x) équivaut à F(x)
= 0.
b. On admet que la
fonction F(x)est
dérivable sur ]0 ; +∞[. Dresser le tableau de variation de la fonction F(x).
(Les limites en 0 et +∞ ne sont pas attendues.)
Dériver : F'(x) =
1 /x -2x+1 = (-2x2+x+1) / x.
x étant positif le signe de F'(x) est celui de
(-2x2+x+1).
-2x2+x+1= 0 ; discriminant D = 1+8=9 ; racines : x1
= (-1-3) / (-4) = 1 et x2 = (-1+3) / (-4) = -0,5.
-2x2+x+1 est positif pour x
appartenant à ]-0,5 ; 1[.
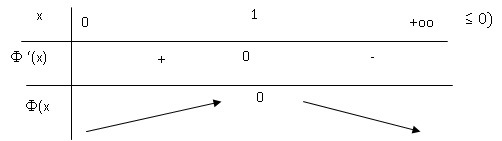
c.
En déduire que, pour tout réel x strictement positif, F(x)
est négatif ou nul.
Ce tableau de variation montre que F(x) possède un maximum nul
pour x = 1. Donc, pour tout réel x
strictement positif, F(x)
est négatif ou nul.
4. a.
La conjecture émise à la question 1. de la partie B est-elle valide ?
Pour tout réel x strictement positif, f
(x) inférieur ou égal à g (x) équivaut à F(x) inférieur ou égal à zéro.
La conjecture est valide.
b.
Montrer que Cf et Cg ont un unique point commun,
noté A.
Sur ]-oo ; 0[, Cf et Cg
n'ont aucun point commun.
Sur[0 ; +oo [ , g(1) = f(1) ; Cf
et Cg ont un seul point commun d'abscisse 1.
c.
Montrer qu’en ce point A, ces deux courbes ont la même tangente.
f(1) = g(1) = 1.
f ′(x) =(1-2x2) exp(1-x2) ; .f
'(1) = -1 ; g' (x) =- e1−x ; g'(1) =
-1.
Au point A, les tangentes aux deux courbes passent par le même point
et, de plus, elles possèdent le même coefficient directeur. Ces
tangentes sont donc confondues.
Partie C.
1. Trouver une
primitive F de la fonction f sur R.
F(x) = -0,5 exp (1-x2).
2. En déduire la
valeur de :
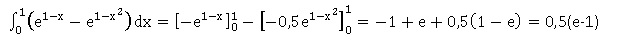
3. Interpréter
graphiquement ce résultat.
C'est l'aire du domaine compris entre les deux courbes et les droites
d'équation x=0 et x=1.
Nlle Calédonie.
On considère la fonction f définie et dérivable sur l’intervalle [0 ;
+oo[ par f (x) = xe−x−0,1.
1. Déterminer la
limite de f en +oo.
Quand x tend vers l'infini ex /x tend vers
l'infini, d'après le cours ; son inverse x /ex tend vers
zéro.
Par suite f(x) tend vers -0,1.
2. Étudier les
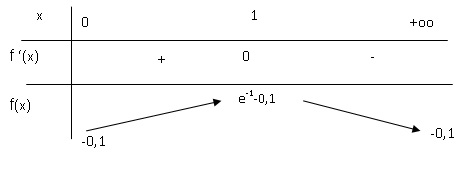
variations de f sur [0 ; +oo[ et dresser le tableau de variations.
Dériver :on pose u =x et v = e-x ; u' =1 et v' = -e-x.
f '(x) = u'v +v'u = e-x -x
e-x = e-x
(1-x).
La dérivée s'annule pour x = 1 ; e-x étant toujours positif,
la dérivée est du signe de (1-x), c'est à dire positive si x est
compris entre 0 et 1 et négative si x est supérieur à 1.
f(x) est croissante sur [0 ; 1[, décroissante sur ]1 ; +oo[ et présente
un maximum pour x= 1.
3.
Démontrer que l’équation f (x) = 0 admet une unique solution notée a sur l’intervalle [0 ; 1].
f(0)=-0,1 est négatif ; f(1) =e-1-0,1
~0,27 ; de plus la fonction est strictement croissante sur [0
; 1]. L’équation f (x) = 0 admet une unique
solution
surcet l’intervalle.
On admet l’existence du nombre réel
strictement positif ß tel que a<
ß et f (ß)= 0.
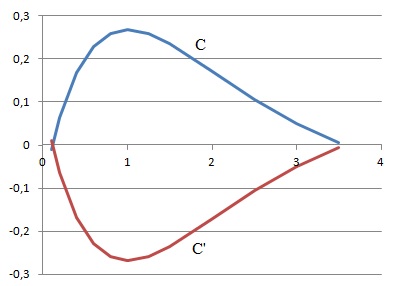
On note C la courbe représentative de la fonction f sur l’intervalle [a ; ß] dans un repère
orthogonal et C ′ la courbe symétrique de C par rapport à l’axe des
abscisses.
L’unité sur chaque axe représente 5 mètres.
Ces courbes sont utilisées pour délimiter un massif floral en forme de
flamme de bougie sur lequel seront plantées des tulipes.
4. Démontrer que la
fonction F, définie sur l’intervalle
[a ; ß]
par F(x) = −(x +1)e−x −0,1x est une primitive de la
fonction f sur l’intervalle
[a ; ß].
Dériver : on pose u = x+1 et v = e-x ; u' = 1 et v' = -e-x
; u'v+v'u =e-x-e-x(1+x) = xe-x.
F '(x) = xe-x-0,1 = f(x).
5.
Calculer, en unités d’aire, une valeur arrondie à 0,01 près de l’aire
du domaine compris entre les courbes C et C ′.
On utilisera les valeurs arrondies à 0,001 près suivantes : a≈ 0,112 et ß ≈ 3,577.
Par raison de symétrie, l'aire cherchée vaut A=2 ( F(ß) -F(a)).
F(3,577) ~-(1+3,577) e-3,577-0,3577 ~ -0,4857 ; F(0,112)
~-(1+0,112) e-0,112-0,0112 ~-1,005 ;
A = 2( -0,4857 +1,005)~1,04 unités d'aire ou 1,04 x25 ~26 m2.
6.
Sachant que l’on peut disposer 36 plants de tulipes par mètre carré,
calculer le nombre de plants de tulipes nécessaire à la réalisation de
ce massif.
26 x36 = 936 tulipes.
|
|