Mathématiques,
nombres complexes, Bac S 2016
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Pondichéry.
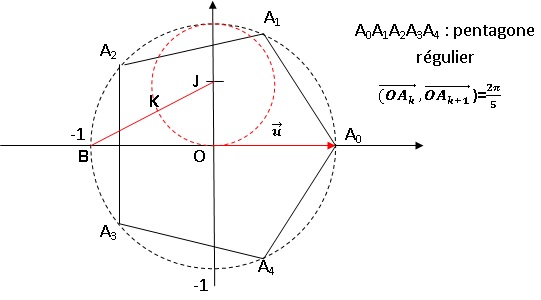
1. On considère le
point B d'affixe -1 et J d'affixe ½i. Le cercle C de centre J et de rayon
½ coupe le segment [BC] en un point K. Calculer BJ puis en déduire BK.
Théorème de Pythagore dans le triangle rectangle OBJ :
BJ2 = OB2 +OJ2= 1 +0,52=1,25=
5 /4 ; BJ =5½ / 2.
BK = BJ -KJ = 5½
/ 2 -½ = (5½-1)
/ 2.
2.a.
Donner sous forme exponentielle l'affixe du point A2.
Justifier brièvement.
A2 appartient au cercle trigonométrique. L'affixe du point A2
a pour module 1 et pour argument 2p/5 +2p/5 = 4p /5 ; zA2 = exp(i 4p/5).
2.b. Démontrer que
BA22 =2 + 2 cos (4p/5).
BA22 = (zA2-zB)2
=( cos(4p/5) + i
sin(4p/5 +1)2
= [ cos(4p/5)+1]2+
sin2(4p/5).
BA22
=cos2(4p/5)+1+2cos(4p/5)+
sin2(4p/5)
=2 + 2 cos (4p/5).
c.
Un logiciel de calcul formel affiche les résultats ci-dessous :
cos(4 p /5)=(-5½-1)
/ 4 ; sqrt((3-sqrt(5)) / 2)=(5½-1) / 2.
"sqrt" signifie racine carrée. En déduire que BA2 = BK.
BA22
=2+(-5½-1)
/ 2=1,5
-5½ / 2 = (3-5½
)/ 2. BA2 =(5½-1) / 2.
3.
Construire à la règle et au compas un pentagone régulier.
Placer le point J sur l'axe des ordonnées et le point B sur l'axe
des abscisses. Construire BJ et le cercle C. Placer le point K à
l'intersection du cercle C
et du segment [BJ].
Le cercle de centre B, de rayon BK, coupe le cercle unitaire en A2
et A3.
Le cercle de centre A2 passant par A3 coupe le
cercle unitaire en A1.
Le cercle de centre A3 passant
par A2 coupe le cercle unitaire en A4.
Amérique
du Nord.
On considère le point A d'affixe 4, le point B d'affixe 4i et les
points C et D tels que ABCD soit un carré de centre O. Pour tout entier
naturel non nul n, on an.ppelle Mn le point d'affixe zn
= (1+i)n.
1. Ecrire le nombre
1 +i sous forme exponentielle.
Module : (12+12)½ = 2½ ;
argument : tan q
= 1 ; q = p /4.
1+i = 2½ exp(i p
/4).
2. Montrer qu'il
existe un entier naturel n0, que l'on précisera, tel que,
pour tout entier supérieur à n0, le point M est à
l'extérieur du carré ABCD.
La distance maximale enre le centre O du carré et un coté du carré est
égale à 4. Le point M est extérieur au carré si OM > 4.
OM = (2½)n >4 ;
½n log 2 >log 4 ; ½n > log 4 / log 2 ; ½n > log 22 / log 2 ; ½n
> 2 ; n >4 ; n0 = 5.
|
| .
. |
|
|
Centre étrangers.
On
veut modéliser dans le plan la coquille d’un nautile à l’aide d’une
ligne brisée en forme de spirale. On s’intéresse à l’aire délimitée par
cette ligne.
On munit le plan d’un repère orthonormal direct.
Soit n un entier supérieur ou égal à 2. Pour tout entier k allant de 0
à n, on définit les
nombres complexes zk =(1+k/n) exp(2 i k p /n) et on note Mk
le point d’affixe zk .
Dans ce modèle, le pourtour du nautile est la ligne brisée reliant tous
les points Mk avec appartenant à [0 ; n].
Partie A : Ligne
brisée formée à partir de sept points
Dans cette partie, on suppose que n = 6. Ainsi, on a zk =(1+k/6) exp(2 i k p /6)
1.
Déterminer la forme algébrique de z1.
z1 =(1+1/6)[
cos( p
/3)+ i sin( p /3) ]= 7 / 6 (0,5 + i 3½
/ 2) =7 / 12 + i 3½ /
12.
2.
Vérifier que z0 et z6 sont des entiers que l’on
déterminera.
z0 =(1+0
/ 6)[ cos( 0)+ i sin(
0) ]=1.
z6 =(1+6/6)[ cos( 6 p /3)+ i sin(
6p /3) ]=2.
3.
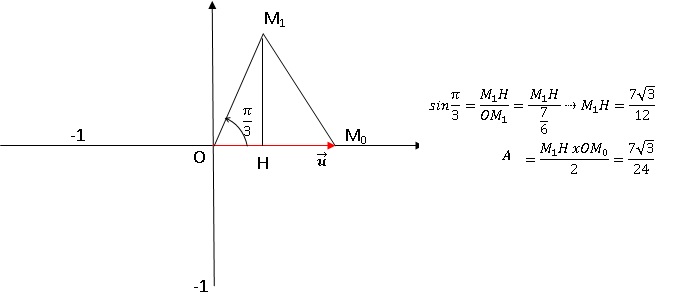
Calculer la longueur de la hauteur issue de M1 dans le
triangle OM0M1 puis établir que l’aire de ce
triangle est égale à 7 x 3½ / 24.
.
Partie B : Ligne brisée formée à
partir de n +1 points.
Dans cette partie, n est un entier supérieur ou égal à 2.
1. Pour tout entier
k tel que k appartenant à [0 ; n], déterminer la longueur OMk
.
OMk est égal au module du
nombre complexe zk, O étant l'origine du repère. OMk
= 1 + k / n.
2. Pour tout entier k tel que k appartenant
à [0 ; n-1], déterminer la mesure des angles suivants :
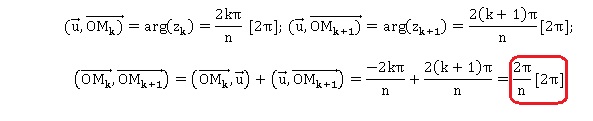
3. Pour
tout entier k tel que k appartenant à [0 ; n-1], et pour tout
entier n supérieur ou égal à 2, démontrer que la longueur de la hauteur
issue de Mk+1 dans le triangle OMkMk+1
est égale à : [1+(k+1) / n] sin ( 2p/n).
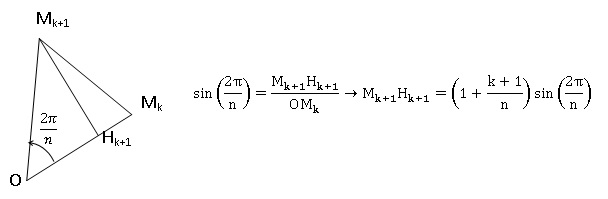
On admet que l’aire du triangle OMkMk+1 est égale
à :
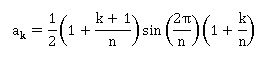
et que l’aire totale délimitée par la ligne brisée est égale à An
= a0 +a1 +···+an−1.
L’algorithme suivant permet de calculer l’aire An lorsqu’on
entre l’entier n :
VARIABLES A est un nombre réel
k est un entier
n est un entier
TRAITEMENT Lire la valeur de n
A prend la valeur 0
Pour k allant de 0 à n-1
A prend la valeur A+0,5 sin ( 2p/n)[1+k/n][1+(k+1)
/ n]
Fin Pour
Sortie Afficher.
On entre dans l’algorithme n = 10
Recopier et compléter le tableau ci-dessous qui illustre le
fonctionnement de l’algorithme.
k
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
A
|
0,323
|
0,711
|
1,17
|
1,705
|
2,322
|
3,027
|
3,826
|
4,726
|
5,731
|
6,848
|
Recopier et compléter les lignes L6 et L13 de l’algorithme ci-après qui
permet
de déterminer le plus petit entier n tel que An supérieur ou
égal à7,2. On ne demande pas de
déterminer n.
L1 VARIABLES : A est un nombre réel
L2 k est un entier
L3 n est un entier
L4 TRAITEMENT : n prend la valeur 2
L5 A prend la valeur 0
L6 Tant que A<7,2
L7 n prend la valeur n +1
L8 A prend la valeur 0
L9 Pour k allant de 0 à n −1
L10 A prend la valeur A+0,5 sin ( 2p/n)[1+k/n][1+(k+1) / n]
Fin Pour
L12 Fin Tant que
L13 SORTIE : Afficher n.
|
|
|
|
Métropole
septembre.
On considère les nombres complexes zn définis pour tout
entier n >0 par la donnée de z0, où z0 est
différent de 0 et de 1, et la relation de récurrence
zn+1 = 1−1 / zn..
1. a. Dans cette
question, on suppose que z0 = 2. Déterminer les nombres z1,
z2, z3, z4, z5 et z6.
z1=1-1/z0=1-0,5 = 0,5.
z2=1-1/z1=1-1/0,5 = -1.
z3=1-1/z2=1+1 =2
= z0.
z4=1-1/z3=1-0,5 =0,5=
z1.
z5=1-1/z4=1-2 =-1= z2.
z6=1-1/z5=1+1 =2=z0.
b. Dans cette
question, on suppose que z0 = i. Déterminer la forme
algébrique des nombres complexes z1, z2, z3,
z4, z5 et z6.
z1=1-1/z0=1-1/i = 1+i.
z2=1-1/z1=1-1/(1+i) =i / (1+i) = i(1-i) / 2= (1+i) / 2.
z3=1-1/z2=1-2/(1+i) =(i-1) / (1+i)= -(1-i)2
/ 2 = i= z0.
z4=1-1/z3=1-1/i =1+i=z1.
z5=1-1/z4=1-1/(1+i) = (1+i) / 2= z2.
z6=1-1/z5=1-2/(1+i) =i= z0.
c. Dans cette
question on revient au cas général où z0 est un complexe
donné.Que peut-on conjecturer pour les valeurs prises par z3n
selon les valeurs de l’entier naturel n ? Prouver cette conjecture.
z3n = z0.
Démonstration par récurrence :
Initialisation
: pour n = 0, on a bien : z3x0 = z0.
Hérédité :
on suppose que pour p entier, z3p =z0, alors :
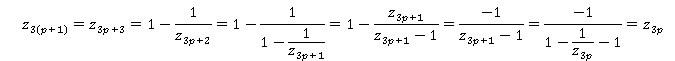
Conclusion
: on a démontré que z3x0 = z0 et que pour tout p
appartenant à N vérifiant z3p =z0, il en résulte
que z3(p+1) = z0 : d'après le principe de
récurrence z3n = z0 quel que soit n entier.
2. Déterminer z2016
dans le cas où z0 = 1+i.
2016 = 3 x 672 = 3 p donc z2016 =z0 = 1+i.
3. Existe-t-il des
valeurs de z0 tel que z0 = z1 ? Que
peut-on dire de la suite (zn) dans ce cas ?
z1 = z0 = 1-1/z0 soit : z02-z0+1=0.
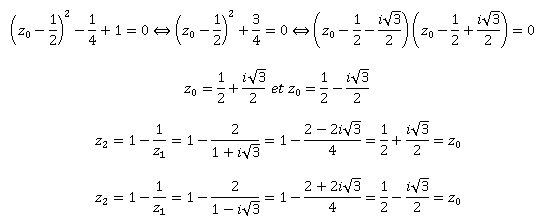
Dans les deux cas, les suites (un) sont constantes.
|
|
Nlle Calédonie.
On se place dans le plan complexe.
Soit f la transformation qui à tout nombre complexe z non nul associe
le nombre complexe f (z) défini par :
f (z) = z +1/z.
On note M le point d’affixe z et M′ le point d’affixe f (z).
1. On appelle A le
point d'affixe a défini ci-dessous..
a. Déterminer la
forme exponentielle de a.
b. Déterminer la
forme algébrique de f (a).
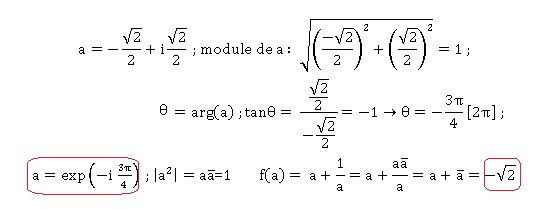
2. Résoudre, dans
l’ensemble des nombres complexes, l’équation f (z)= 1.
z+1 /z = 1 ; z2+1= z ; z2-z
+1= 0 ; D =
1-4=-3 = 3 i2.
L'équation admet deux solutions z1 = (1-i 3½) / 2
et z2 = (1+i 3½) / 2.
3.
Soit M un point d’affixe z du cercle C de centre O et de rayon 1.
a. Justifier que
l’affixe z peut s’écrire sous la forme z = exp( iµ) avec µ un nombre
réel.
Le point M appartient au cercle de rayon 1, son module est donc égal à
1.
Alors la forme exponentielle de z est
z = exp( iµ) avec µ un nombre réel.
b.
Montrer que f (z) est un nombre réel.
f(z) = exp(i µ) + 1 / exp(i µ) =exp(i µ)+exp(-i µ) = cos µ + i
sin µ + cos (-µ) + i sin (-µ) = 2 cos µ +i sin µ-i sin µ = 2 cos µ.
4. Décrire et
représenter l’ensemble des points M d’affixe z tels que f (z) soit un
nombre réel.
On pose z = x +iy.
f(z) = x+iy +1 /(x+iy) = [(x+iy)2 + 1] / ( x+iy) = [x2
-y2+2ixy +1] / (x+iy).
Multiplier numérateur et dénominateur par x-iy :
f(z) = [x2 -y2+2ixy
+1](x-iy) / (x2+y2).
Développer le numérateur et annuler la partie imaginaire :
Numérateur : (x2 -y2+1)x
+2xy2+i[ 2x2y - x2
y +y3-y]
2x2y - x2
y +y3-y = 0 ; y(2x2 - x2
+y2-1 )= 0.
x2
+y2=1. Equation du cercle de centre O et de rayon unité.
y = 0 : axe des abscisses, à l'exception du point O, z ne peut
pas être nul.
|
|