Mathématiques,
géométrie dans l'espace, bac S 2015
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Pondichéry
Soit
un cube ABCDEFGH d’arête 1. Dans le repère indiqué, on considère les
points M, N et P de coordonnées respectives M (1 ; 1 ; 0,75) , N (0 ;
0,5 ; 1) et P( 1 ; 0 ; -1,25).
1. PlacerM, N et P sur la figure donnée en annexe.
2. Déterminer les
coordonnées des vecteurs suivants. En déduire que les points M, N
et P ne sont pas alignés.
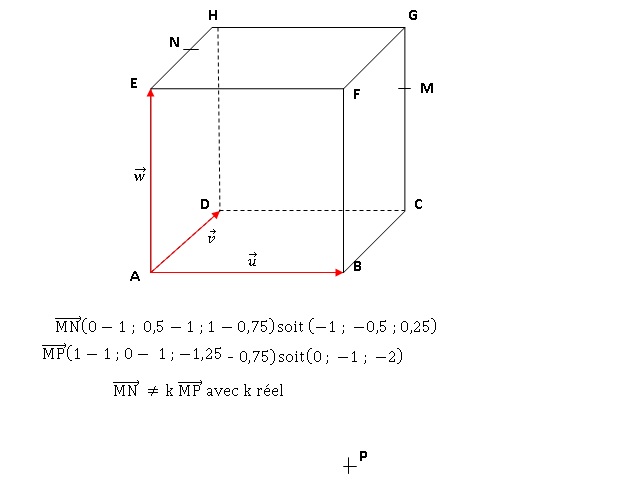
Ces vecteurs ne sont pas colinéaires ; les droites (MN) et (MP) ne sont
pas parallèles ; les points M, N et P ne sont pas alignés.
3. On considère
l’algorithme suivant :
Saisir xM, yM, zM,xN, yN,
zN,xP, yP, zP
d prend la valeur xN −xM
e prend la valeur yN − yM
f prend la valeur zN −zM
g prend la valeur xP −xM
h prend la valeur yP − yM
i prend la valeur zP −zM
k prend la valeur d ×g +e ×h+ f ×i
a. Exécuter à la
main cet algorithme avec les coordonnées des points M, N et P données
ci-dessus.
d
|
e
|
f
|
g
|
h
|
i
|
k
|
-1
|
-0,5
|
0,25
|
0
|
-1
|
-2
|
0
|
b. À quoi
correspond le résultat affiché par l’algorithme ? Qu’en déduire pour le
triangle MNP ?
Cet algorithme calcule le produit scalaire des deux vecteurs cités
ci-dessus. Ce produit scalaire étant nul, ces vecteurs sont
orthogonaux. Le triangle MNP est rectangle en M.
4. On considère
l’algorithme 1. Le compléter pour qu’il teste et affiche si un triangle
MNP est rectangle et isocèle en M.
l prend la valeur d2+e2+f2
m prend la valeur g2+h2+i2
Si k=0 et si l =m
afficher " le triangle MNP est rectangle isocèle en M"
Sinon afficher " le triangle MNP n'est pas rectangle ou n'est pas
isocèle en M".
5. On considère le vecteur n (5 ;
−8 ; 4) normal au plan (MNP).
a. Déterminer une
équation cartésienne du plan (MNP)..
On considère un point Q(x ; y ; z) de ce plan.
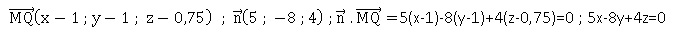
b. On considère la
droite D passant
par F et de vecteur directeur n .
Déterminer une représentation paramétrique de la droite D.
x =5t +a ; y = -8t +b ; z = 4t+c.
La droite passe par F(1 ; 0 1), d'où a = 1 ; b = 0 et c = 1.
x =5t +1 ; y =
-8t ; z = 4t+1.
6. Soit K le point d’intersection du
plan (MNP) et de la droite D.
a. Démontrer que
les coordonnées du point K sont 4 /7 ; 24 /35 ;23 / 35.
K appartient au plan (MNP) : 5xK-8yK+4zK
= 0.
K appartient à la droite D : xK = 5t+1 ; yK =
-8t ; zK = 4t+1.
5(5t+1) +64t+4(4t+1)=0
25t+5+64t+16t+4=0 ; 105t = -9 ; t = -3/35.
xK = 5t+1 =-3/7+1=4/7 ; yK
= -8t=24/35 ; zK = -12/35+1=23/35.
b. On donne FK =(27 /35)½.
Calculer le volume du tétraèdre MNPF.
Base : triangle MNP, rectangle en M.
Hauteur : FK ( la droite (FK) est orthogonale au plan ( MNP).
V = aire de base fois hauteur /3 = MN xMP /2 xFK / 3.
MN= [(-1)2+(-0,5)2+0,252]½=(21/16)½
= 21½/4.
MP= [02+(-1)2+(-2)2]½=5½.
V = (5 x 21 x 27 / 35)½ / 24 = 9 /24 =3 / 8 m3.
Liban.
ABCDEFGH est un
cube.
I
est le milieu du segment [AB], J est le milieu du segment [EH], K est
le milieu du segment [BC] et L est le milieu du segment [CG].
On munit l’espace du repère orthonormé.
1. a. Démontrer que
la droite (FD) est orthogonale au plan (IJK).
b. En déduire une
équation cartésienne du plan (IJK).
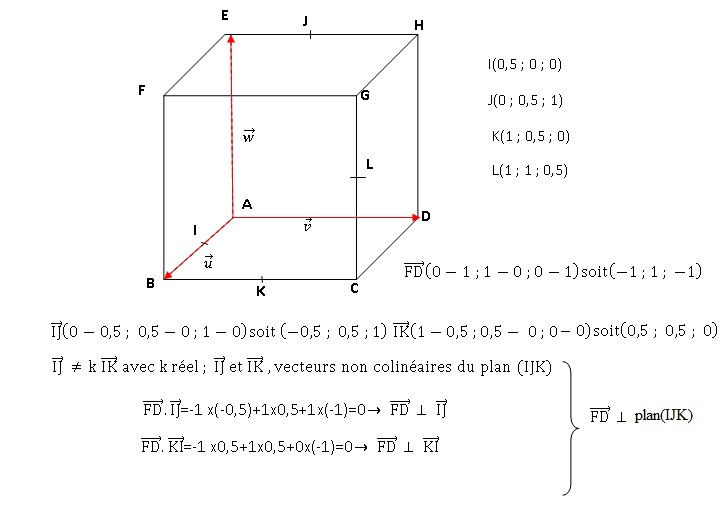
-x +y-z= a ; I(0,5 ; 0 ; 0) appartient au plan (IJK), d'où a = 0,5.
-x+y-z=0,5.
2. Déterminer une
représentation paramétrique de la droite (FD).
La droite (FD) est dirigée suivant le vecteur de coordonnées (-1 ; 1 ;
-1) :
x = -t+a ; y = t+b ; z = -t+c.
Cette droite passe par D(0 ; 1 ; 0) : a=c=0 et b = 1.
x = -t ; y = t+1 ; z = -t.
3. Soit M le point
d’intersection de la droite (FD) et du plan (IJK). Déterminer les
coordonnées du point M.
M appartient au plan (IJK) : -xM+yM+zM=0,5.
M appartient à la droite (FD) : xM=-t ; yM = 1+t
; zM =-t.
t+1+t-t=0,5 ; t=-0,5.
xM=0,5 ; yM = 0,5 ; zM
=0,5.
4. Déterminer la nature du triangle
IJK et calculer son aire.
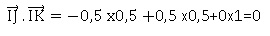
Le triangle IJK est rectangle en I.
IJ = [(-0,5)2+0,52+12]½=6½/2.
IK = [0,52+0,52+02]½=2½/2.
Aire de ce triangle : IJ x IK / 2 = 3½/4.
5. Calculer le
volume du tétraèdre FIJK.
Aire de base = aire du triangle IJK ; hauteur = FM = [(-0,5)2+0,52+(-0,5)2]½=3½/2.
Volume = aire de base x hauteur / 3 = 3½/4 x3½/6=3
/24=1/8..
6. Les droites (IJ) et (KL)
sont-elles sécantes ?
La
droite (IJ) est dirigée suivant le vecteur de coordonnées (-0,5 ; 0,5 ;
1 ) ; de plus elle passe par le point I(0,5 ; 0 ; 0 ). Une
représentation paramétrique de cette droite est :
x = -0,5 t +0,5 ; y = 0,5 t ; z = t.
La droite (KL)
est dirigée suivant le vecteur de coordonnées (0 ; 0,5 ;0,5 ) ;
de
plus elle passe par le point K(1; 0,5 ; 0 ). Une représentation
paramétrique de cette droite est :
x = 1 ; y = 0,5 t'+0,5 ; z =0,5t'.
Dans l'hypothèse où les droites sont sécantes, les coordonnées du point
d'intersection vérifient :
-0,5t+0,5 =1 soit t = -1 ; 0,5t =0,5t'+0,5 ; t = 0,5t' soit t'=-2.
Ces droites sont sécantes au point de coordonnées ( 1 ; -0,5 ; -1).
|
| .
. |
|
|
Polynésie.
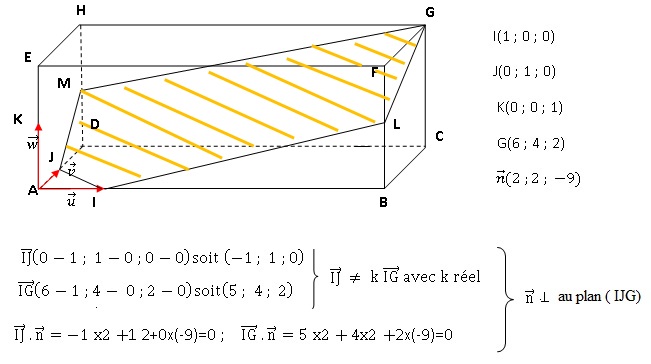
On considère le pavé droit ABCDEFGH ci-dessous, pour
lequel AB = 6, AD = 4 et AE = 2.
I, J et K sont les points définis ci-dessous.
1. Vérifier que le
vecteur de coordonnées(2 ; 2 ; -9) est normal au plan (IJG).
2. Déterminer une
équation du plan (IJG).
Le vecteur de coordonnées (2 ; 2 ; -9) est orthogonal au plan ( IJG) :
2x+2y-9z=a.
Le point I(1 ; 0 ; 0) appartient à ce plan : 2 +0+0=a ;
2x+2y-9z=2.
3. Déterminer les
coordonnées du point d’intersection L du plan (IJG) et de la droite
(BF).
Cette droite est dirigée suivant le vecteur (0 ; 0 ; 2) et passe par la
point B(6 ; 0 ; 0). Une représentantion paramétrique de cette droite
est : x=6 ; y=0 ; z = 2t.
L appartient au plan (IJG) :
2xL+2yL-9zL=2.
L appartient à la droite ( BF) : xL=6 ; yL=0 ; zL = 2t.
2x6 +2x0-9x2t=2 soit t =5 / 9.
L( 6 ; 0 ; 10 /9).
4. Tracer la
section du pavé ABCDEFGH par le plan (IJG).
|
|
|
|
Amérique du Nord.
Dans l’espace, on considère une pyramide SABCE à base carrée ABCE de
centre O.
Soit D le point de l’espace tel que le repère dessiné soit un repère
orthonormé. Le point S a pour coordonnées (0 ; 0 ; 3) dans ce repère.
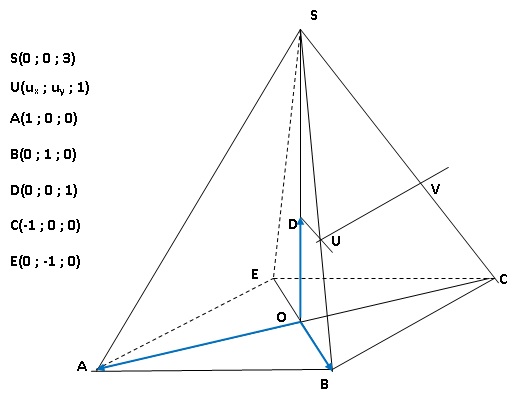
Partie A .
1. Soit U le point
de la droite (SB) de cote 1. Construire le point U sur la figure.
Utiliser le théorème de Thalès dans les triangles OBS et DUS.
D'une part, D et U ont la même cote ( 1) et d'autre part , O et B ont
la même cote (0).
(DU) et (OB) sont parallèles.
OS / OD = BS / BU = 3 ; BU = BS / 3.
2. Soit V le point
d’intersection du plan (AEU) et de la droite (SC).Montrer que les
droites (UV) et (BC) sont parallèles. Construire le point V sur la
figure.
Les plans (AUE) et (BCS) sont sécants selon la droite ( UV) ; la base
étant carrée, (BC), incluse dans le plan ( BCS), est parallèle à (AE),
incluse dans le plan ( AEU).
En appliquer le théorème du toit, on en dédduit que (BC est parallèle à
( UV).
3. Soit K le point
de coordonnées ( 5 / 6 ; -1 /6 ; 0). Montrer que K est le pied de la
hauteur issue de U dans le trapèze AUVE.
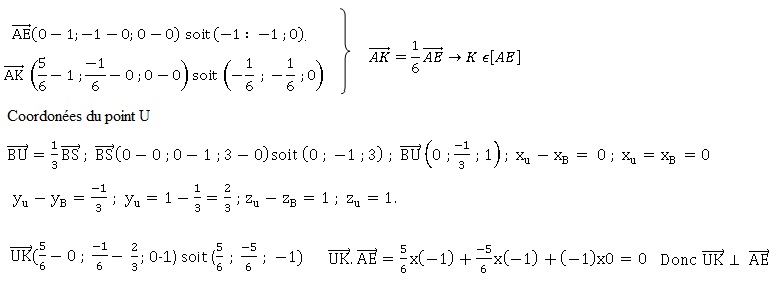
Partie B.
Dans cette partie, on admet que l’aire du quadrilatère AUVE est 5x43½
/18.
1. On admet que le
point U a pour coordonnées (0 ; 2 /3 ;1).
Vérifier que le plan (EAU) a pour équation 3x −3y +5z −3 = 0.
E(0 ; -1 ; 0 ) ; 3xE −3yE +5zE =
0-3(-1)+0 = 3.
Les coordonnées du point E vérifient 3x −3y +5z −3 = 0, donc E
appartient à ce plan.
A(1 ; 0 ; 0 ) ; 3xA −3yA +5zA =
3-3(0)+5x0 = 3.
Les coordonnées du point A vérifient 3x −3y +5z −3 = 0, donc A
appartient à ce plan.
U(0 ; 2/3 ; 1 ) ; 3xU −3yU +5zU =
3x0-3(2/3)+5x1 = 3.
Les coordonnées du point U vérifient 3x −3y +5z −3 = 0, donc U
appartient à ce plan.
2. Donner une
représentation paramétrique de la droite (d) orthogonale au plan (EAU)
passant par le point S.
Coordonnées d'un vecteur orthogonal au plan ( EAU) : 3 ; -3 ; +5.
La droite (d) est dirigée suivant le vecteur de coordonnées (3 ; -3 ;
5) et passe par le point S ( 0 ; 0 ; 3).
Représentaation paramétrique de la droite (d) : x = 3t ; y = -3t ; z =
5t+3 avec t réel.
3. Déterminer les
coordonnées de H, point d’intersection de la droite (d) et du plan
(EAU).
H appartient à la droite (d) : xH = 3t ; yH = -3t
; zH = 5t+3
H appartient au plan ( EAU) : 3xH −3yH +5zH
−3 = 0.
9t +9t+25t+15-3 = 0 ; 43 t = -12 ; t = -12 / 43.
H ( -36 / 43 ; 36 / 43 ; 69/43).
4. Le plan (EAU)
partage la pyramide (SABCE) en deux solides. Ces deux solides ont-ils
le même volume ?
Volume de la pyramide : 1 /3 aire de base x hauteur ;
AC = 2 ; AE = 2 / 2½ ; aire du carré : 2 m2.
Volume de la pyramide : V = 1/3 x2 x3 = 2 m3 ; ½V = 1 m3.
Volume du tétraèdre (SAUVE) : 1 /3 aire de base x hauteur SH.
SH2 =(-36 /43)2 + (36/43)2 +(69 /43 -3)2
=6192 / 1849 ; SH2 = 144 / 43 ; SH = 12 /
43½.
1/3x5x43½ /18 x12 / 43½ =60 /54 = 10 / 9 m3
, différent de 1 m3.
Ce plan ne partage pas la pyramide en deux solides de même volume.
|
|
Polynésie septembre.
ABCDEFGH est un cube. I est le
milieu de [AB], J est le milieu de [HD] et K est le milieu de [HG].
1.
Démontrer que le vecteur CE est un vecteur normal au plan (IJK).
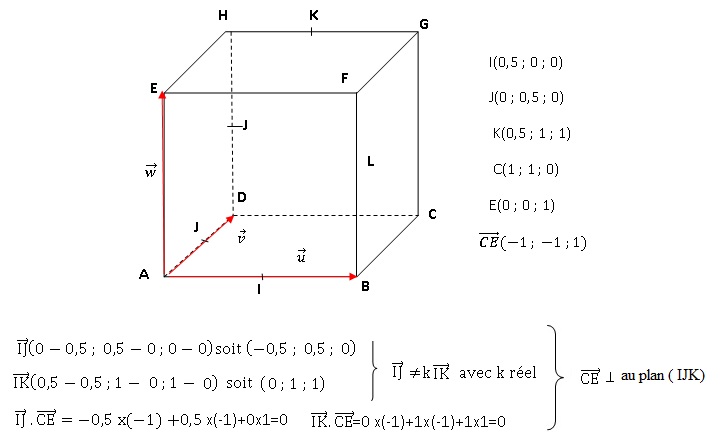
Equation paramétrique de ce plan : -x-y+z = a ; ce plan passe par I(0,5
; 0 ; 0) ; d'où a= -0,5.
2. Démontrer que la
droite (BD) est parallèle au plan (IJK).
cette droite est dirigée suivant le vacteur Bd de coordonnées (1 ; -1 ;
0) et passe par le point B(1 ; 0 ; 0). Une représentation
paramétrique de cette droite est :
x = t+1 ; y = -t ; z = 0.
Dans l'hypothèse où la droite ( BD) et le plan (IJK) sont sécants :
-t-1-(-t) +0 = -0,5 ; -1 diffère de -0,5.
La droite et le plan ne sont pas sécants. La droite et le plan ne sont
pas confondus car, quel que soit t,
-t-1-(-t) +0 diffère de -0,5.
La droite (BD) et le plan (IJK) sont donc parallèles.
3.
Soit M(x, ; y ; z ) un point de la droite (CE). Quelle est la position
du point M sur la droite (CE) pour laquelle le plan (BDM) est parallèle
au plan (IJK) ?
On fait l'hypothèse que ces deux plans sont parallèles, c'est à dire,
tous deux perpendiculaires au vecteur de coordonnées (-1 ; -1 ; 1).

Le point M appartient au plan ( BDM) ; k-1 +k-1+k = -1 soit
k =1/3.
Par suite M( 2/3 ; 2/3 ; 1/3)
Antilles septembre.
On se place dans le repère orthonormé dessiné.
1. a. Montrer que
la droite (DB) admet pour représentation paramétrique
x = s ; y = 1−s, z = 0 , où s décrit l’ensemble R des nombres réels.
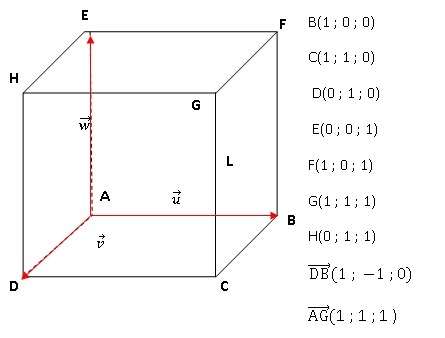
Cette droite est dirigée suivant le vecteur de coordonnées ( 1 ; -1 ;
0) et passe par le point D(0 ; 1 ; 0).
Une représentation paramétrique de cette
droite est : x = s ; y = 1-s ; z = 0.
b.
Montrer que les points de la droite (AG) sont les points de coordonnées
(t ; t ; t ) où t est un réel.
Cette droite est dirigée suivant le vecteur de coordonnées (1 ; 1 ; 1 )
et passe par le point A(0 ; 0 ; 0).
Une représentation paramétrique de cette droite est : x= t ; y=t ; z=t.
Un point N( xN ; yN ; zN) de cette
droite est tel que : xN= t ; yN=t
; zN=t.
2.
Soit M un point quelconque de la droite (DB) et N un point quelconque
de la droite (AG).
Démontrer que la droite (MN) est perpendiculaire aux deux droites (AG)
et (DB) si et seulement si M et N ont pour coordonnées respectives
(0,5 ; 0,5 ; 0) et (1/3 ; 1/3 ; 1/3).
M appartient à la droite (DB) : M(s ; 1-s ; 0). N appartient à la
droite (AG) : N(t ; t ; t ).
par suite M et N ont pour coordonnées respectives
(0,5 ; 0,5 ; 0) et (1/3 ; 1/3 ; 1/3).
3. Soit
s et t deux réels quelconques. On note M(s ; 1−s ; 0) un point de la
droite (DB) et N(t ; t ; t ) un point de la droite (AG).
a. Montrer que MN2
= 3(t − 1/3)2+2(s-0,5)2+1/6.
MN2 =(t-s)2 + (t-1+s)2
+t2 =t2+s2-2ts+t2+1+s2-2t-2s+2ts
+t2=3t2+1-2t
+2s2-2s = 3(t2+1/9-2t
/3)+2(s2-s ) +2/3 = 3(t
− 1/3)2+2(s2-s
+1/4)+1/6= 3(t − 1/3)2+2(s-0,5)2+1/6.
b.
En déduire la position des points M et N pour laquelle la distance MN
est minimale.
Que peut-on dire de la droite (MN) dans ce cas ?
MN2 est la somme detrois nombres positifs. MN2
est minimale si chaque terme de la somme est minimum.
(t − 1/3)2est minimum si t
− 1/3 = 0 soit t = 1/3 ; (s-0,5)2 est
minimum si s − 0,5 = 0 soit s = 0,5.
Pour ces valeurs la droite (MN) est perpendiculaire aux droites ( BD)
et (AG).
Nlle Calédonie.
1. a. Vérifier que
le plan d’équation x + y +z = 1 est le plan (BDE).
b. Montrer que la
droite (AG) est orthogonale au plan (BDE).
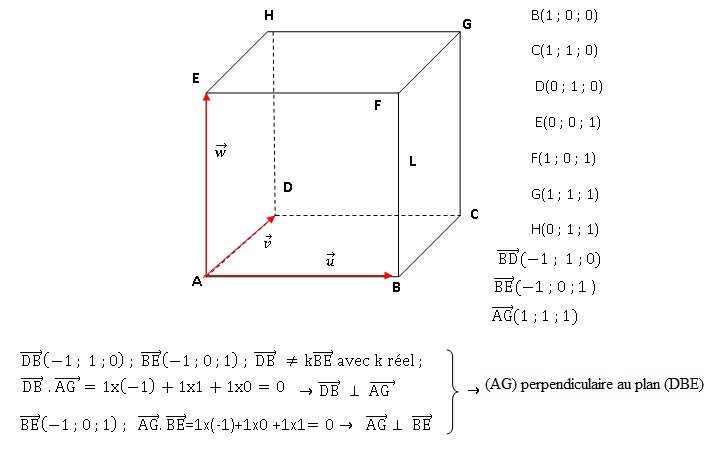
Une représentation paramétrique du plan ( DBE) est x +y +z = a.
Le point B(1 ; 0 ; 0) appartient à ce plan : 1+0+0 = a soit a = 1.
c. Montrer que
l’intersection de la droite (AG) avec le plan (BDE) est le point K de
coordonnées (1/3 ; 1/3 ; 1/3).
La droite (AG) est dirigée suivant le vecteur de coordonnées (1 ; 1 ;
1) et passe par le point A(0 ; 0 ; 0). Une représentation
paramétrique de cette droite est x = t ; y = t ; z =
t avec t réel.
K appartient à cette droite : xK = t ; yK = t ; zK
= t.
K appartient au plan ( BDE) : xK +yK
+zK
= 1 ; t + t +t = 1 soit t = 1/3.
2.
Le triangle BDE est-il équilatéral ?
Ce triangle ayant trois côtés égaux est équilatéral.
3. Soit M un point
de l’espace.
a. Démontrer que si
M appartient au plan (BDE), alors AM2 = AK2+MK2.
M (x ; y ; z) est tel que x+y+z=1. AM2 = x2+y2+z2.
AK2 = 3 (1/3)2 = 1/3. MK2=(1/3-x)2
+(1/3-y)2 +(1/3-z)2=
x2+y2+z2 +1/3-2/3(x+y+z)=x2+y2+z2
+1/3-2/3 = =x2+y2+z2
-1/3.
AK2+MK2 = x2+y2+z2
-1/3 +1/3 = x2+y2+z2
=AM2.
b.
En déduire que si M appartient au plan (BDE), alors AM2 est
supérieur ou égal à AK2.
MK2 >0 donc AM2
est supérieur ou égal à AK2.
c.
Soient x, y et z des réels quelconques. En appliquant le résultat de la
question précédente au point M de coordonnées (x ; y ; z),montrer que
l’implication
(P1) est vraie.
(P1) (x+y+z=1) implique (
x2+y2+z2
supérieur ou égal à 1/3).
Si les coordonnées de M vérifient x+y+z=1, alors M appartient au plan
(BDE) ; donc AM2
est supérieur ou égal à AK2.
AM2 = x2+y2+z2.
AK2 = 1/3 ;
x2+y2+z2
supérieur ou égal à 1/3.
|
|