Mathématiques,
suite numérique, algorithme, bac S 2015
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Pondichéry.
Partie A
Soit (un) la suite définie par son premier terme u0
et, pour tout entier naturel n, par la relation un+1 = aun
+b (a et b réels non nuls tels que a différent de1.
On pose, pour tout entier naturel n, vn = un
−b/(1−a)..
1. Démontrer que,
la suite (vn) est géométrique de raison a.
vn+1 =un+1-b/(1-a) = aun+b-b/(1-a)=
aun-ab/(1-a) = a[un -b/(1-a)]=a vn.
vn+1 =a
vn indique que la suite (vn) est géométrique de
raison a.
2. En déduire que si a appartient à
l’intervalle ]−1 ; 1[, alors la suite (un) a pour limite b
/(1−a).
vn = anv0 ;
a appartient à l’intervalle ]−1 ; 1[, alors an
tend vers zéro si n tend vers l'infini : donc vn tend vers
zéro.
Or vn = un −b/(1−a),
donc un tend vers b/(1-a) quand n tend vers l'infini.
Partie B.
En
mars 2015, Max achète une plante verte mesurant 80 cm. On lui conseille
de la tailler tous les ans, au mois de mars, en coupant un quart de sa
hauteur. La plante poussera alors de 30 cma u cours des douze mois
suivants.
Dès qu’il rentre chez lui,Max taille sa plante.
1. Quelle sera la
hauteur de la plante en mars 2016 avant que Max ne la taille ?
80 x3 / 4 +30 = 90 cm.
2. Pour tout entier
naturel n, on note hn la hauteur de la plante, avant sa
taille, en mars de l’année (2015+n).
a. Justifier que,
pour tout entier naturel n, hn+1 = 0,75hn +30.
La taille correspond à la multiplication par 0,75 et la pousse annuelle
est de 30 cm.
b. Conjecturer à
l’aide de la calculatrice le sens de variations de la suite (hn).
u0 = 80 cm ; u1 = 90 ; u2 = 0,75 x90
+30 = 97,5 ; la suite semble être croissante.
Démontrer cette conjecture (on pourra utiliser un raisonnement par
récurrence).
Initialisation
: h0 < h1 est vraie.
Hérédité :
on suppose que hp < hp+1.
0,75 hp < 0,75 hp+1 entraîne 0,75
hp +30< 0,75 hp+1 +30 entraîne hp+1
<hp+2.
La propriété est donc héréditaire.
Conclusion
: la propriété est vraie au rang zéro et héréditaire : donc hn < hn+1 pour tout n entier.
c. La suite (hn) est-elle
convergente ? Justifier la réponse.
Si la suite converge vers l, par continuité,
l'égalité hp+1=0,75 hp+30 donne en passant aux
limites à l'infini :
l = 0,75 l +30 soit l = 120.
La taille de la plante sera inférieure à 1,20 m.
Liban.
On définit la suite
(un) de la façon suivante, pour tout entier naturel n.
1. Calculer u0.
2. a. Démontrer
que, pour tout entier naturel n, un+1 +un = 1
/(n+1).
b. En déduire la
valeur exacte de u1.
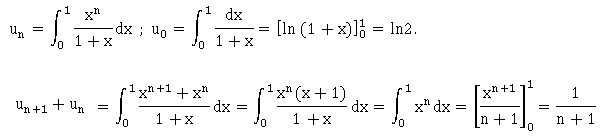
u1+u0=1 ; u1 =1-ln2.
3. a. Recopier et
compléter l’algorithme ci-dessous afin qu’il affiche en sortie le terme
de rang n de la suite (un) où n est un entier naturel saisi
en entrée par l’utilisateur.
Variables : i et n sont des entiers naturels
u est un réel
Entrée : Saisir n
Initialisation : Affecter à u la valeur ln2
Traitement : Pour i variant de 1 à n
Affecter à u la valeur 1/i-u
Fin de Pour
Sortie : Afficher u
b. À l’aide de cet
algorithme, on a obtenu le tableau de valeurs suivant :
n
|
0
|
1
|
2
|
3
|
4
|
5
|
10
|
50
|
100
|
un
|
0,693
|
0,3069
|
0,1931
|
0,1402
|
0,1098
|
0,0902
|
0,0405
|
0,0099
|
0,0050
|
Quelles conjectures
concernant le comportement de la suite (un) peut-on émettre ?
La suite est décroissante et converge vers zéro.
4. a. Démontrer que
la suite (un) est décroissante.
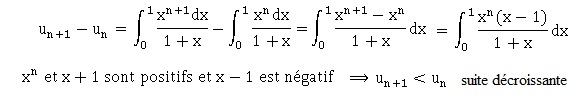
b. Démontrer que la
suite (un) est convergente.
La suite estt décroissante et tous ces termes sont positifs. D'après le
théorème de la convergence monotone, la suite converge.
5. On appelle ℓ la
limite de la suite (un). Démontrer que ℓ = 0.
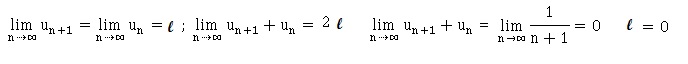
|
| .
. |
|
|
Centres étrangers.
Soit a un nombre réel fixé non nul.
Le but de cet exercice est d’étudier la suite (un) définie par :
u0 = a et, pour tout n de N, un+1 = e2un
−eun .
On remarquera que cette égalité peut aussi s’écrire : un+1 =
eun (eun −1).
1. Soit g la
fonction définie pour tout réel x par :
g (x) = e2x −ex −x.
a. Calculer g ′(x)
et prouver que, pour tout réel x : g ′(x) = (ex −1) (2ex
+1).
g'(x)=2e2x-ex -1= 2e2x-ex -1=2ex
ex-2ex
+ex-1=2ex(ex-1)+ex-1=(ex −1) (2ex +1).
b.
Déterminer les variations de la fonction g et donner la valeur de son
minimum.
(2ex
+1) est toujours positif . Le signe de g'(x) est celui
de ex-1.
si x <0, g'(x) est négative et g(x) est strictement décroissante.
Si x>0, g'(x) >0 et g(x) est strictement croissante.
Si x=1, g'(x)=0 et g(x) présente un minimum égal à 0.
c. En remarquant que un+1
−un = g (un), étudier le sens de variation de la
suite (un).
un+1
−un =e2un
−eun −un est positif pour n entier.
un+1 >un , la
suite est croissante.
2.
Dans cette question, on suppose que a est négatif ou nul.
a. Démontrer par
récurrence que, pour tout entier naturel n, un est négatif
ou nul.
Initialisation
: u0 =a est vrai.
Hérédité :
on suppose la propriété vraie au rang p, up inférieur ou
égal à 0.
up+1=eup(eup-1) ; eup est
positif et eup est compris entre 0 et1 ; (eup-1)est donc négatif ou nul.
up+1est
donc négatif ou nul ; la propriété est vraie au rang p+1.
Conclusion :
la propriété est vraie au rang zéro et héréditaire, donc pour tout entier naturel n, un
est négatif ou nul.
b. Déduire des questions précédentes
que la suite (un) est convergente.
La suite est croissante et majorée par zéro. D'après le théorème de la convergence monotone,
la suite converge
c. Dans le cas où a
vaut 0, donner la limite de la suite (un).
u0=0 et un supérieure ou égale à u0.
De plus un est négatif ou nul ; donc un =0.
La suite est constante, égale à zéro ; sa limite est nulle.
3. Dans cette question, on suppose
que a > 0.
La suite (un) étant croissante, la question 1. permet
d’affirmer que, pour tout entier naturel n, un supérieur ou
égal à a.
a. Démontrer que,
pour tout entier naturel n, on a : un+1 −un
supérieur ou égal à g (a).
un+1
−un = g (un).
Or
a est positif et inférieur ou égal à un ; de plus g
est strictement croissante sur [0 ; +oo[.
Donc g(0) <g(a) <=g(un).
Pour tout n, g(un) est supérieur ou égal à g(a).
un+1
−un
supérieur ou égal à g (a).
b.
Démontrer par récurrence que, pour tout
entier naturel n, on a :
un supérieur ou égal à a +n ×g (a).
Initialisation
: u0 = a est vrai.
Hérédité :
on suppose la propriété vraie au rang p :
up supérieur ou égal à a +p ×g (a).
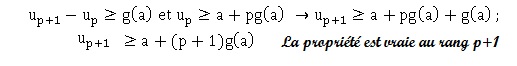
Conclusion
: la propriété est vraie au rang zéro et est héréditaire.
un supérieur ou égal à a +n ×g (a) pour tout n.
c.
Déterminer la limite de la suite (un).
a étant positif et 0 étant le minimum de la fonction g, g(a) est
positif.
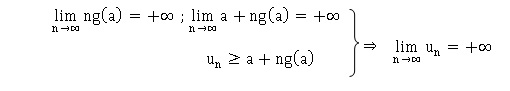
4. Dans cette
question, on prend a = 0,02.
L’algorithme suivant a pour but de déterminer le plus petit entier n
tel queun >M, où M désigne un réel positif. Cet
algorithme est incomplet.
Variables n est un entier,
u et M sont deux réels
u prend la valeur 0,02
Initialisation n prend la valeur 0
Saisir la valeur de M
Traitement Tant que u<=M
u prend la valeur e2u-eu
n prend la valeur n+1
Fin tant que
Sortie Afficher n
a. Sur la copie,
recopier la partie « Traitement » en la complétant.
b. À l’aide de la
calculatrice, déterminer la valeur que cet algorithme
affichera si M = 60.
u35 = 2,13 et u36 = 62,35. L'algorithme affiche : 36.
|
|
|
|
Polynésie.
Soit (vn) la suite définie par v1
= ln(2) et, pour tout entier naturel n non nul, vn+1 = ln(2-e-vn)
On admet que cette suite est définie pour tout entier naturel n non nul.
On définit ensuite la suite (Sn) pour tout entier naturel n
non nul par :
Sn = v1 +v2 +···+vn.
Le but de cet exercice est de déterminer la limite de (Sn).
Partie A.
Conjectures à l’aide d’un algorithme
1. Recopier et
compléter l’algorithme suivant qui calcule et affiche la valeur de Sn
pour une valeur de n choisie par l’utilisateur :
Variables : n, k entiers
S, v réels
Initialisation : Saisir la valeur de n
v prend la valeur ln(2)
S prend la valeur ln(2)
Traitement : Pour k variant de 2.à
n. faire
v prend la valeur ln(2-e-v)
S prend la valeur S +v
Fin Pour
Sortie : Afficher S
2. À l’aide de cet
algorithme, on obtient quelques valeurs de Sn. Les valeurs
arrondies au dixième sont données dans le tableau ci-dessous :
n
|
10
|
100
|
1000
|
10
000
|
100
000
|
Sn
|
2,4
|
4,6
|
6,9
|
9,2
|
11,5
|
En expliquant votre démarche, émettre une conjecture quant au
comportement de la suite (Sn).
Les valeurs du tableau indiquent que la suite (Sn) est
croissante.
Partie B. Étude
d’une suite auxiliaire
Pour tout entier naturel n non nul, on définit la suite (un)
par un = evn .
1. Vérifier que u1
= 2 et que, pour tout entier naturel n non nul, un+1 = 2−1/un.
v1 = ln2 ; u1= eln2 = 2.
un+1 = evn+1 = exp[ ln(2-e-vn)]=2-e-vn
2-1 / evn=2-1/un.
2. Calculer u2,
u3 et u4. Les résultats seront donnés sous forme
fractionnaire.
u2 = 2-1/u1 = 2-1/2=3/2.
u3 = 2-1/u2 = 2-2/3=4/3.
u4 = 2-1/u3 = 2-3/4=5/4.
3. Démontrer que,
pour tout entier naturel n non nul, un =(n +1) / n
Démonstration par récurrence :
Initialisation
: propriété vraie pour n =2.
Héridité :
on suppose la propriété vraie au rang p : up=(p+1) / p.
up+1 = 2-1/up = 2-p/(p+1) = (2p+2-p) /
(p+1)=(p+2) / (p+1). La propriété est vraie au rang p+1.
Conclusion
: la propriété est vraie au rang 2 et héréditaire.
Pour tout entier naturel n non nul, un =(n +1) / n.
Partie C. Étude de
(Sn)
1. Pour tout entier
naturel n non nul, exprimer vn en fonction de un,
puis vn en fonction de n.
un = evn ; vn=ln(un) =ln[
(n +1) / n].
2. Vérifier que S3
= ln(4).
v1 =ln2 ; v2=ln(1,5) ; v3 =ln(4 /3).
S3 = ln(2) +ln(1,5) +ln(4 / 3) = ln (2 x 1,5 x4 /3) =ln(4).
3. Pour tout entier
naturel n non nul, exprimer Sn en fonction de n. En déduire
la limite de la suite (Sn).
Sn = v1 +v2...+vn =ln(2)
+ln(3 / 2) + ln( 4 /3) +...+ln[n+1) / n] =ln [2 x3 / 2 x4 /
3...x(n+1) /n] = ln(n+1).
ln(n+1) tend vers l'infini lorsque n tend vers l'infini. La suite
(Sn) est divergente.
|
|
Antilles.
Soit
n un entier naturel non nul.
Partie A.
On considère l’algorithme suivant :
Variables : k et p sont des entiers naturels
u est un réel
Entrée : Demander la valeur de p
Traitement
Affecter à u la valeur 5
Pour k variant de 1 à p
Affecter à u la valeur 0,5u +0,5(k −1)−1,5
Fin de pour
Sortie : Afficher u
Faire fonctionner cet algorithme pour p = 2 en indiquant les valeurs
des variables à chaque étape.
Quel nombre obtient-on en sortie ?
u
|
k
|
|
5
|
1
|
|
0,5x5-1,5=1
|
2
|
|
0,5x1+0,5(2-1)-1,5=
-0,5
|
|
|
A la sortie, on obtient -0,5.
Partie B.
Soit (un) la suite définie par son premier terme u0
= 5 et, pour tout entier naturel n par : un+1 = 0,5un
+0,5n −1,5.
1. Modifier
l’algorithme de la première partie pour obtenir en sortie toutes les
valeurs de un pour n variant de 1 à p.
On considère l’algorithme suivant :
Variables : k et p sont des entiers naturels
u est un réel
Entrée : Demander la valeur de p
Traitement
Affecter à u la valeur 5
Pour k variant de 1 à p
Affecter à u la valeur 0,5u +0,5(k −1)−1,5
Afficher u
Fin de pour
Sortie : Afficher u
2.
À l’aide de l’algorithme modifié, après avoir saisi p = 4, on obtient
les résultats suivants :
n
|
1
|
2
|
3
|
4
|
un
|
1
|
-0,5
|
-0,75
|
-0,375
|
Peut-on affirmer, à partir de ces résultats, que la suite (un)
est décroissante ? Justifier.
u4 > u3, on ne peut pas affirmer que la suite
est décroissante.
3. Démontrer par
récurrence que pour tout entier naturel n supérieur ou égal à 3, un+1
> un.
Que peut-on en déduire quant au sens de variation de la suite (un)
?
Initialisation : u4
>u3, la propriété est vrai au rang 3.
Hérédité :
on suppose que up+1 >
up.
up+1 = 0,5up
+0,5p −1,5.
up+2 = 0,5up+1
+0,5(p+1) −1,5.
up+2 -up+1
=0,5up+1 -
0,5up +0,5 = 0,5 (up+1
-up +1)
Or up+1 >
up. donc up+2 -up+1
>0 ; up+2 >up+1.
La proprièté est vraie au rang p+1.
Conclusion
: la propriété est vrai au rang3 et héréditaire.
Pour tout entier naturel n supérieur ou
égal à 3, un+1 > un.
La suite est croissante à partir du rang 4.
4.
Soit (vn) la suite définie pour tout entier naturel n par vn
= 0,1un−0,1n+0,5.
Démontrer que la suite (vn) est géométrique de raison 0,5 et
exprimer alors vn en fonction de n.
un+1 = 0,5un +0,5n
−1,5.
vn+1 = 0,1un+1−0,1(n+1)+0,5
= 0,1(0,5un +0,5n −1,5)−0,1(n+1)+0,5=0,05un+0,05n-0,15-0,1n-0,1+0,5=0,05un-0,05n+0,25
vn+1 =0,5(0,1 un
-0,1n+0,5)=0,5 vn.
La suite (vn) est donc géométrique de raison 0,5.
u0=5 ; v0=0,1x5-0,1x 0+0,5=1 et vn
=0,5n.
5.
En déduire que, pour tout entier naturel n, un = 10×0,5n
+n −5.
vn = 0,1un−0,1n+0,5
; 0,1un=vn
+0,1n-0,5 ; un = 10vn+n-5 ;
un = 10x 0,5n+n-5
.
6.
Déterminer alors la limite de la suite (un).
La limite de 0,5n est nulle quand n tend vers l'infini. La
limite de la suite (un) est égale à +oo quand n tend vers
l'inifini.
|
|