Mathématiques,
fonction logarithme, exponentielle bac S 2015
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Pondichéry.
A. Soit f la
fonction définie sur R par f(x) =3 /(1+e-2x), sa courbe
représentative C et la droite D
d'équation y=3.
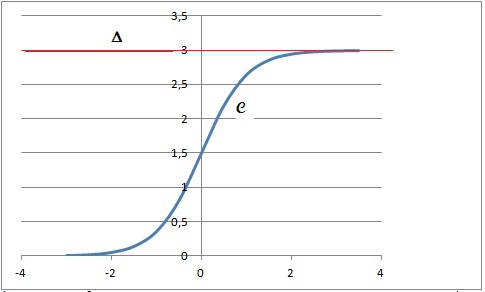
1. Démontrer que la
fonction f est strictement croissante sur R.
On pose u = 1+e-2x ; u'=-2 e-2x ; f '(x) = -u' /
u2 = 6e-2x /(1+e-2x)2.
e-2x est positif, f '(x) est positive sur R. De plus f '(x)
ne s'annule pas.
Donc la fonction f est strictement croissante sur R.
2. Justifier que la
droite D est
asymptote à la courbe C.
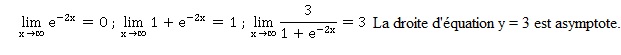
3. Démontrer que
l’équation f (x) = 2,999 admet une unique solution a sur R. Déterminer un
encadrement de a
d’amplitude 10−2.
2,999 (1+e-2x )= 3 ; 1+e-2x
=3/2,999 ; e-2x
=3/2,999 -1 =( 3-2,999) / 2,999 =3,3344 10-4.
-2x = ln(3,3344
10-4) =-8,00604 ; x = 4,003.
a est
compris entre 4,00 et 4,01.
B. Soit h la
fonction définie sur R par h(x) = 3− f (x).
1. Justifier que
la fonction h est positive sur R.
h(x) = 3 [ 1-1 /(1+e-2x) ] = 3 e-2x
/ (1+e-2x).
e-2x étant positif, h(x) est positive sur R.
2.
On désigne par H la fonction définie sur R par H(x) = −1,5ln(1+e-2x)
Démontrer que H est
une primitive de h sur R.
On
dérive en posant u = 1+e-2x ;
u' = -2 e-2x.
H'(x) = -1,5 u' / u = 3e-2x / (1+e-2x) = h(x).
3. Soit a un réel
strictement positif.
a. Donner une
interprétation graphique de l’intégrale I.
Aire positive de la surface comprise entre la courbe C', les
droites d'équation x=0, x=a et l'axe des abscisses.
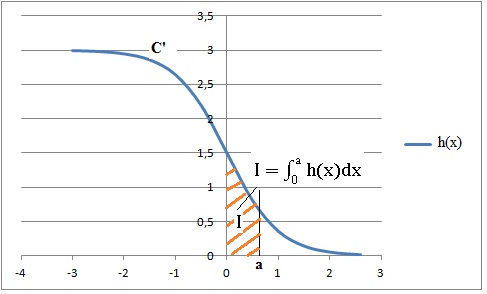
b. I =
H(a)-H(0) = -1,5 ln(1+e-2a) +1,5 ln(1+1) = 1,5 [ ln2 -ln(1+e-2a)]=
1,5 ln [2 / (1+e-2a)].
c. On note D
l’ensemble des points M(x ; y) du plan défini par
x positif ou nul et par y appartenant à [f(x) ; 3 ]
Déterminer l’aire, en unité d’aire, du domaine D.
L'aire du domaine D est la limite en l'infini de I =1,5 ln [2 / (1+e-2a)].
Le terme en exponentielle tend vers zéro quand x tennd vers
l'infini.
L'aire du domaine D est égale à : 1,5 ln 2~1,04 unités d'aire.
Amérique
du Nord.
Partie A
Soit u la fonction définie sur ]0 ; +oo[ par u(x) = ln(x)+x −3.
1. Justifier que la
fonction u est strictement croissante sur l’intervalle ]0 ; +oo[.
u'(x) =1 /x +1 = (1+x) /x.
u'(x) est positive sur ]0 ; +oo[ ; de plus
u'(x) ne s'annule pas sur cet intervalle.
u(x) est strictement croissante sur cet intervalle.
2. Démontrer que l’équation u(x) = 0
admet une unique solution a
comprise entre 2 et 3.
u(2) =ln2 +2+3 = ln 2-1 ~ -0,31 ; u(3) = ln 3 ~1,1.
u(2) <0, u(3) >0, u est continue, le théorème des valeurs
intermédiaires s'applique.
0 possède un antécédent par u dans [2 ; 3 ]. De plus u est strictement
monotone sur cet intervalle, l'antécédent a est unique.
3. En déduire le
signe de u(x) en fonction de x.
u(x) <0 si x appartient à ]0 ; a [ et u(x) >0 si x
appartient à ]a ;
+oo[.
Partie B.
Soit f la fonction définie sur l’intervalle ]0 ; +oo[ par f (x) =(1-1 /
x) ( ln x -2) +2.
On appelle C la courbe représentative de la fonction f dans un repère
orthogonal.
1. Déterminer la
limite de la fonction f en 0.
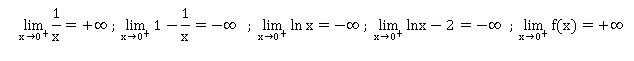
2. a. Démontrer
que, pour tout réel x de l’intervalle ]0 ; +oo[, f ′(x) =u(x) / x2
où u est la fonction définie dans la partie A.
On pose v = 1-1/x et w = ln x -2 ; v' = 1/x2 ; w'=1/x.
v'w +w'v = (ln x-2) / x2 +1/x-1/x2 = (ln x -2
+x-1) / x2 = u(x).
b. En déduire le
sens de variation de la fonction f sur l’intervalle ]0 ; +oo[.
x2 est positif ; le signe de f '(x) est celui de u(x).
u(x) <0 si x appartient à ]0 ; a [ et u(x) >0 si x
appartient à ]a ;
+oo[.
f(x) est strictement décroissante si
x appartient à ]0 ; a
[ et f(x) est strictement croissante si x appartient à ]a ; +oo[.
Partie C
Soit C ′ la courbe d’équation y = ln(x).
1. Démontrer que,
pour tout réel x de l’intervalle ]0 ; +oo[, f (x)−ln(x) =(2−ln(x)) / x.
f (x)−ln(x) =
(1-1 / x) ( ln x -2) +2 -ln x = ln x -ln x
/ x -2 +2 /x +2 -ln x ;
f (x)−ln(x) =
-ln x / x +2 /x = (2-ln x) / x.
En déduire
que les courbes C et C ′ ont un seul point commun dont on déterminera
les coordonnées.
f (x)−ln(x) =0
; 2 = ln x ; solution unique x = e2 ; y = ln( e2)
= 2.
2. On admet que la fonction H
définie sur l’intervalle ]0 ; +oo[ par H(x) =0,5[ ln(x)]2
est une primitive de la fonction h définie sur l’intervalle ]0 ; +oo[
par ln(x) / x..
Calculer l'intégrale I suivante et intrerpréter graphiquement le
résultat.
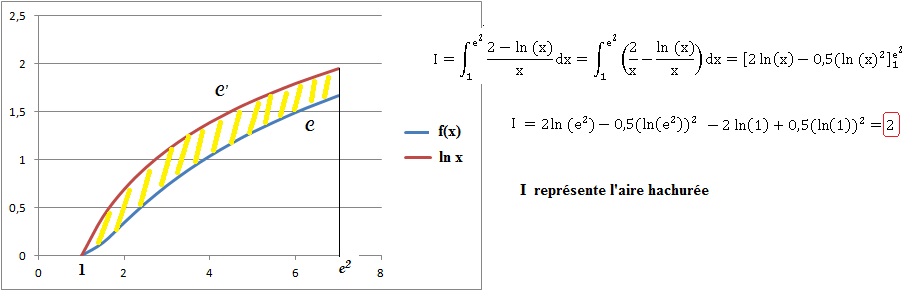
|
| .
. |
|
|
Polynésie.
Le directeur d’un zoo souhaite faire construire un
toboggan pour les pandas.
Partie A.
Modélisation
Le profil de ce toboggan est modélisé par la courbe C représentant la
fonction f définie sur l’intervalle [1 ; 8] par
f (x) = (ax +b)e−x où a et b sont deux entiers naturels.
La courbe C est tracée ci-dessous dans un repère orthonormé dont
l’unité est le mètre.
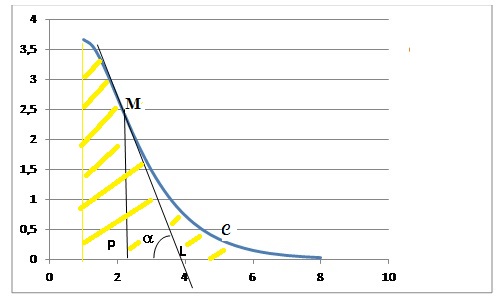
1. On souhaite que
la tangente à la courbe C en son point d’abscisse 1 soit horizontale.
Déterminer la valeur de l’entier b.
Calculer f '(x) et chercher la valeur de b qui annule cette dérivée en
x=1.
On pose u = ax+b et v = e-x ; u' = a ; v' = -e-x
; f '(x)=u'v+v'u = ae-x-(ax+b)e-x =0 pour x=1.
-a-b+a = 0 ; b = 0.
2. On souhaite que
le haut du toboggan soit situé entre 3,5 et 4 mètres de haut.
Déterminer la valeur de l’entier a.
f(1) = a e-1 = 2,718 a , compris entre 3,5 et 4.
a est compris entre 3,5 e et 4e soit entre 9,5 et 10,9.
Le seul entier compris entre ces valeurs est 10.
Partie B Un
aménagement pour les visiteurs
On admet dans la suite que la fonction f introduite dans la partie A
est définie pour tout réel x ∈ [1 ; 8] par
f (x) = 10xe−x .
Le mur de soutènement du toboggan sera peint par un artiste sur une
seule face, hachurée sur le schéma en début d’exercice. Sur le devis
qu’il propose, celui-ci demande un forfait de 300 euros augmenté de 50
euros par mètre carré peint.
1. Soit g la
fonction définie sur [1 ; 8] par g (x) = 10(−x −1)e−x .
Déterminer la fonction dérivée de la fonction g .
On pose u = -x-1 et v = e-x ; u'=-1 ; v'= -e-x ;
u'v +v'u = -e-x+(x+1)e-x = xe-x; g'x)
= 10x e-x=f(x)
g(x) est une primitive de f(x).
2. Quel est le montant du devis de l’artiste ?
f(x) étant positive, l'aire hachurée vaut : A = g(8)-g(1)=10 ( -9
e-8 +2e-1)=10 (0,73576-0,00302)~7,3274 m2.
Coût : 300 + 50 x7,3274 = 666,37 €.
Partie C Une
contrainte à vérifier
Des raisons de sécurité imposent de limiter la pente maximale du
toboggan.
On considère un point M de la courbe C , d’abscisse différente de 1. On
appelle a l’angle
aigu formé par la tangente en M à C et l’axe des abscisses.
Les
contraintes imposent que l’angle a soit inférieur à 55 degrés.
1.
On note f ′ la fonction dérivée de la fonction f sur l’intervalle [1 ;
8].On admet que, pour tout x de l’intervalle [1 ; 8], f ′(x) = 10(1−x)e−x
.
Étudier les variations de la fonction f ′ sur l’intervalle [1 ; 8].
Calcul de f'' (x) : u = 1-x ; v = e-x ; u' = -1 ; v' = -e-x
; u'v +v'u = -e-x+(x-1)e-x =(x-2)e-x ;
f''(x) = 10(x-2)e-x.
e-x est positive, le signe de f''(x) est celui de x-2.
Si x<2, f ''(x) est négative : f '(x) est décroissante.
Si x >2, f ''(x) est positive : f ' (x) est croissante.
si x=2, f '(x) présente un minimum f '(2)= -1,35.
2. Soit x un réel
de l’intervalle ]1 ; 8] et soit M le point d’abscisse x de la courbe C
. Justifier que tan a
=|f '(x)|
Equation de la
tangente à la courbe C : y = f '(x) x + b.
La tangente passe en L(X ; 0) ) ; 0=f '(x) X + b ; b =
-X f '(x).
y = f '(x) (x-X).
tan a =PM
/ |PL| =
f(x) / |X-x| = |f '(x)|.
3. Le toboggan est-il conforme aux contraintes imposées ?
|f '(x)|max =1,35 ; amax = 53,5,
valeur inférieure à 55. Le tobogan est conforme.
|
|
|
|
Métropole.
Une municipalité a décidé d’installer un module de
skateboard dans un parc de la commune.
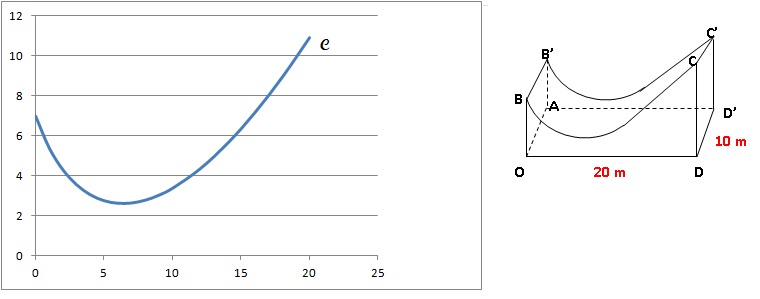
Le profil du module de skateboard a étémodélisé à partir d’une photo
par la fonction f définie sur l’intervalle [0 ; 20] par
f (x) = (x +1) ln(x +1)−3x +7.
On note f ′ la
fonction dérivée de la fonction f et C la courbe représentative de la
fonction f.
Partie 1.
1. Montrer que pour
tout réel x appartenant à l’intervalle [0 ; 20], on a f ′(x) = ln(x
+1)−2.
On pose u = x+1 et v = ln (x+1) ; u' = 1 ; v' = 1/(1+x). ; u'v
+v'u = ln(x+1) +(x+1) / (x+1) = ln(x+1) +1.
f '(x) = ln(x+1) +1 -3 = ln(x+1)-2.
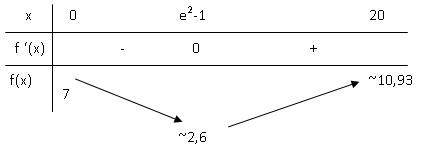
2. En déduire les
variations de f sur l’intervalle [0 ; 20] et dresser son tableau de
variation.
f '(x) est nulle pour ln(x+1)=2 ; x+1 = e2 ; x = e2-1.
f '(x) est négative sur [0 ; e2-1[ et positive sur ]e2-1
; 20]
f '(x) est strictement décroissante sur [0 ; e2-1[ et
strictement croissante sur ]e2-1 ; 20]
f(x) présente un minimum en x = e2-1.
3. Calculer le
coefficient directeur de la tangente à la courbe C au point d’abscisse
0.
f '(0) =ln(1)-2 = -2.
La valeur absolue de ce coefficient est appelée l’inclinaison du module
de skateboard au point B.
4. On admet que la
fonction g définie sur l’intervalle [0 ; 20] par
g (x) =0,5(x+1)2 ln(x+1)-0,25x2-0,5x
a pour dérivée la fonction g ′ définie sur l’intervalle [0 ; 20] par g
′(x) = (x+1) ln(x+1).
Déterminer une primitive de la fonction f sur l’intervalle [0 ; 20].
f(x) = g'(x)-3x+7 ; on note F(x) une primitive de f(x) :
F(x) = g(x) -1,5x2 +7x.
F(x) =0,5(x+1)2 ln(x+1)-1,75x2+6,5x.
Partie 2.
Les trois questions de cette partie sont indépendantes
1. Les propositions
suivantes sont-elles exactes ? Justifier les réponses.
P1 : La différence de hauteur entre le point le plus haut et le point
le plus bas de la piste est au moins égale à 8 mètres.
10,93-2,6 = 8,33, valeur supérieure à 8. P1 est vraie.
P2 : L’inclinaison de la piste est presque deux fois plus grande en B
qu’en C.
Valeur absolue de f '(0) = 2 ; f '(20) = 1,044. P2 est vraie.
2. On souhaite
recouvrir les quatre faces latérales de ce module d’une couche de
peinture rouge. La peinture utilisée permet de couvrir une surface de 5
m2 par litre. Déterminer, à 1 litre près, le nombre minimum
de litres de peinture nécessaires.
Face OABB' rectangulaire : 7 x 10 = 70 m2.
Face CC'DD' rectangulaire : 10,93 x 10 = 109,3 m2.
Aire face avant =aire face arrière = F(20)-F(0) =0,5(21)2ln21-1,75
x202+6,5x20 - (0,5ln(1)-0-0 )=671,31 -700+130=101,31 m2.
Aire totale : 70 +109,3 +101,31+101,31 = 381,92 m2.
Volume de peinture : 381,92 / 5 =76,34 ~77 L.
3. On souhaite
peindre en noir la piste roulante, autrement dit la surface supérieure
du module.
Afin de déterminer une valeur approchée de l’aire de la partie à
peindre, on considère dans le repère (O, I, J) du plan de face, les
points
Bk (k ; f (k)) pour k variant de 0 à 20. Ainsi B0
= B.
On décide d’approcher l’arc de la courbe C allant de Bk à Bk+1
par le segment [BkBk+1].
Ainsi l’aire de la surface à peindre sera approchée par la somme des
aires des rectangles du type BkBk+1B′k +1B′k.
a. Montrer que pour
tout entier k variant de 0 à 19, BkBk+1
=[1+[f(k+1)-f(k)]2 ]½.
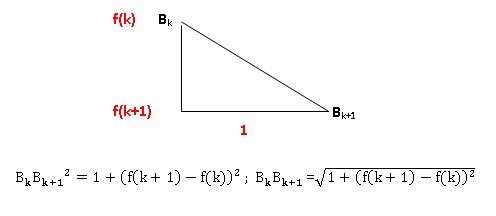 . .
b. Compléter
l’algorithme suivant pour qu’il affiche une estimation de l’aire de la
partie roulante.
Variables S : réel
K : entier
Fonction f : définie par f (x) = (x +1) ln(x +1)−3x +7
Traitement S prend pour valeur 0
Pour K variant de 0 à 19
S prend pour valeur S+10[1+[f(k+1)-f(k)]2 ]½
Fin Pour
Sortie Afficher S.
|
|
Antilles.
Soit
n un entier naturel non nul.
On considère la fonction fn définie et dérivable sur l’ensemble R des
nombres réels par fn(x) = x2e−2nx .
On note Cn la courbe représentative de la fonction fn
dans un repère orthogonal.
Partie A
: Étude de la fonction f1.
1. La fonction f1 est définie sur R
par f1(x) = x2e−2x .
On admet que f1 est dérivable sur R et on note f1′
sa dérivée.
a. Justifier que
pour tout réel x, f1′(x) = 2xe−2x (1−x).
On pose u = x2 et v = e-2x ; u'=2x ; v' = -2e-2x.
u'v + v'u = 2xe-2x -2x2e-2x =2x(1-x)e-2x.
b. Étudier les
variations de la fonction f1 sur R.
La dérivée s'annule pour x=0 et x = 1.
e-2x étant toujours positive, la dérivée a le signe de
x(1-x).
x<0, f1'(x) est négative, f1x est strictement
décroissante.
x appartenant à ]0 ; 1[, f1'(x) est positive, f1(x)
est strictement croissante.
x>1, f1'(x) est négative, f1(x) est
strictement décroissante.
f1(x) présente un minimum nul en x=0 et un maxximum en x=1.
c. Déterminer la
limite de f1 en −oo.
Le terme en exponentielle tend vers l'infini et le terme x2
tend vers l'infini : f1(x) tend vers l'infini.
d. Vérifier que
pour tout réel x, f1(x) =(x /ex)2. En
déduire la limite de f1 en +oo.
Le terme en exponentielle croît plus vite que x au voisinage de
l'infini. f1(x) tend vers zéro quand x tend vers l'infini.
2. En utilisant un
système de calcul formel, on trouve qu’une primitive F1 de
la fonction f1 est donnée par F1(x) = −e−2x(0,5x2+0,5x+0,25).
En déduire la valeur exacte de I1.
I1 = F1(1)-F1(0) = -e-2(0,5+0,5+0,25)+e0(0+0+0,25)=0,25e
-1,25e-2.
Partie B : Étude de
la suite (In)
1. Soit n un entier
naturel non nul.
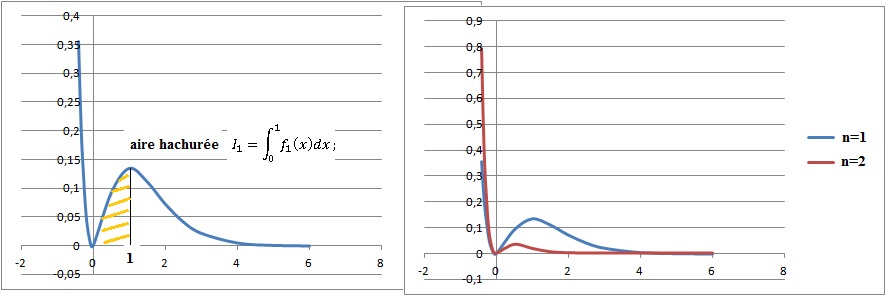
a. Interpréter
graphiquement la quantité In.
Aire hachurée ci-dessus.
b. Émettre alors
une conjecture sur le sens de variation et sur la limite éventuelle de
la suite (In ). Expliciter la démarche qui a mené à cette
conjecture.
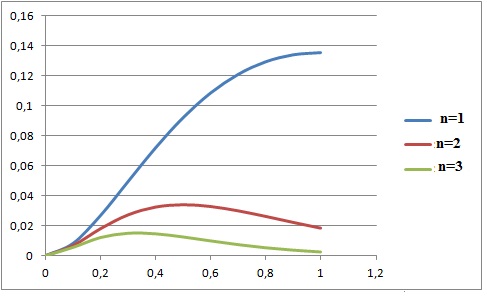
Les intégrales entre 0 et 1 sont décroissantes. Les termes de la suite
ontt des valeurs de plus en plus petites, jusquà atteinfre une valeur
nulle..
2. a.
Justifier que, pour tout entier naturel n non nul et pour tout réel x
appartenant à [0 ; 1], fn+1(x) = e−2x fn(x).
fn+1(x) =x2 e-2(n+1)x
= x2 e-2nx e-2x
= e−2x fn(x).
b.
En déduire, pour tout entier naturel n non nul et pour tout réel x
appartenant à [0 ; 1], que fn+1(x)
est inférieur ou égal à fn(x).
e−2x est
inférieur ou égal à 1 sur [0 ; 1] ;
fn(x)étant positif, e−2x
fn(x) est inférieur ou égal à
fn(x).
c.
Déterminer alors le sens de variation de la suite (In).
D'après la positivité de l'intégration, la suite (In) est
décroissante.
3. Soit n un entier naturel non nul.
a. Justifier que
pour tout entier naturel n non nul et pour tout réel x appartenant à [0
; 1], fn (x) est supérieur ou égal à zéro et inférieur ou
égale à e-2nx.
b. En déduire un encadrement de la suite (In), puis sa limite.
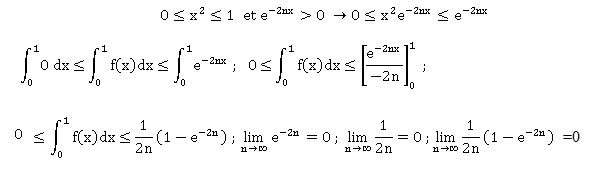
D'après le théorème
des gendarmes, la suite (In) est convergente et sa limite en
l'infini est égale à zéro.
Nlle Calédonie.
Pour chaque réel a, on considère la fonction fa définie sur l’ensemble
des nombres réels R par
fa (x) = ex−a −2x +ea.
1. Montrer que pour
tour réel a, la fonction fa possède un minimum.
f 'a(x) =ex-a-2 ;
ex-a est toujours positif. Si ex-a est inférieure
à 2, la dérivée est négative et fa(x) est strictement
décroissante.
Si ex-a est supérieure à 2, la
dérivée est positive et fa(x) est strictement croissante.
Si ex-a =2, soit x = ln2 +a, la
dérivée est nulle et fa(x) présente un minimum.
2. Existe-t-il une
valeur de a pour laquelle ce minimum est le plus petit possible ?
fa(ln2+a)=eln2-a+a -2ln2-2a +ea=2-2ln2-2a+ea.
Etudiier les variations de la fonction g(a) = 2-2ln2-2a+ea.
g'(a)= -2+ea. ea
est toujours positif. Si ea est inférieure à 2, la dérivée
est négative et g(a) est strictement décroissante.
Si ea est supérieure à 2, la
dérivée est positive et g(a) est strictement croissante.
Si ea
=2, soit a = ln2 +a, la dérivée est nulle et g(a) présente
un minimum.
g(ln2) = 2-2ln2-2ln2+2 =4-4ln2.
Amérique du sud.
A. Dans le plan
muni d’un repère orthonormé, on désigne par Cu la courbe
représentative de la fonction u définie sur l’intervalle ]0 ; +∞[ par :
u(x) = a +b / x +c /x2 où a,b et c sont des réels fixés.
On a tracé sur le graphique ci-dessous la courbe Cu et la
droite D d’équation y = 1.
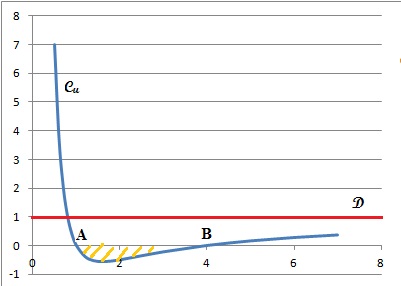
On précise que la courbe Cu passe par les points A(1 ; 0) et
B(4 ; 0) et que l’axe des ordonnées et la droite D sont asymptotes à la
courbe Cu.
1. Donner les
valeurs de u(1) et u(4).
u(1) =0 ; u(4)=0.
2. Donner la
limite en +oo de u(x). En déduire la valeur de a.
b / x +c /x2 tendent vers
l'infini quand x tend vers l'infini.
u(x) tend vers a quand x tend vers l'infini. La droite d'équattion y =
a est asymptote : a=1.
3.
En déduire que, pour tout réel x strictement positif, u(x) = 1-5/x +4/x2.
u(1) = a+b+c =0 avec a = 1 ; b = -1 -c.
u(4) = 1+b/4 +c/16 = 0 ; 16 + 4b +c = 0. ; 16 -4-4c+c=0 ; c = 4 ; par
suite b = -5.
Partie B.
Soit f la fonction définie sur l’intervalle ]0 ; +∞[ par : f (x) = x
−5lnx −4 /x.
1. Déterminer la
limite de f (x) lorsque x tend vers 0. On pourra utiliser sans
démonstration le fait que la limite de x ln(x) = 0 quand x tend vers
zéro.
f(x) =[ x2-5x ln(x) -4 ] / x.
La limite de x2-5x ln(x) -4 est égale à -4
quand x tend vers zéro. La limite de f(x) est égale à -oo quand x
tend vers zéro.
2. Déterminer la
limite de f (x) lorsque x tend vers +oo.
f(x) = x[1-5ln(x) / x -4/x2]
Quand x tend vers l'infini :
la limite de ln(x) x est égale à zéro ; la limite de 4/x2
est égale à zéro ; la limite de 1-5ln(x)
/ x -4/x2 est égale à 1.
La limite de f(x) est égale à +oo lorsque x tend vers l'infini.
3.
Démontrer que, pour tout réel x strictement positif, f ′(x) = u(x).
f '(x) = 1-5 /x +4/x2 = u(x).
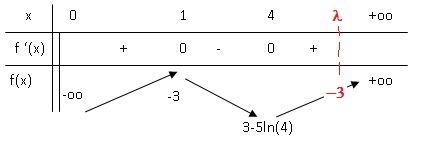
En déduire le tableau de variation de la fonction f en précisant les
limites et les valeurs particulières.
u(x) s'annule pour x=1 et x=4 ; u(x) est positive pour x compris entre
0 et1 : f(x) est croissante sur ]0 ; 1 ].
u(x) est négative entre 1 et 4 : f(x) est déctroissante sur [1 ; 4 ].
u(x) est positive sur [4 ; +oo[ : f(x) est croissante sur cet
intervalle.
Partie C.
1. Déterminer
l’aire A, exprimée en unité d’aire, du domaine hachuré sur le graphique
de la partie A.
A = f(1)-f(4)= -3 -(3-5 ln(4)) = 5 ln(4) -6 unités d'aire.
2. Pour tout réel l supérieur ou égal à 4, on
note Al l’aire,
exprimée en unité d’aire, du domaine formé par les points M de
coordonnées (x ; y) telles que
x appartienne à [4 ; l] et y appartienne à [0 ;
u(x)].
Existe-t-il une valeur de l
pour laquelle Al
=A ?
Al
= f(l)-f(4) = f(l) -
3+5 ln(4)= 5 ln(4) -6 ;
f(l)
=-3.
D'après le tableau de variation de f(x), il existe une valeur unique de
l.
|
|