Décomposer en éléments simples une fraction rationnelle. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Exemple 1. Factorier le polynome : P(x) = x3-3x+2. P(1) = 0 ; P(x) = (x-1)(ax2+bx+c). Développer : P(x) =ax3+bx2+cx -ax2-bx-c =ax3+(b-a)x2+(c-b)x -c = x3-3x+2. On identifie  : a=1 ; c=-2 ; b=1. P(x) = (x-1)(x2+x-2). x2+x-2= (x-1)(dx+e)) = dx2-dx+ex-e = dx2+x(e-d)-e. On identifie : d=1 et e =2. Par suite P(x) = (x-1)2(x+2). Décomposer en éléments simples la fraction rationnelle :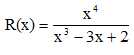 Le degré du polynome figurant au numérateur étant supérieur à celui du polynome figurant au dénominateur, faire la division. 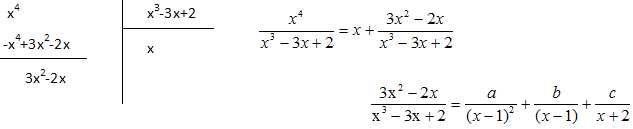Réduire au même dénominateur ; le numérateur vaut : N= a(x+2) +b(x-1)(x+2) +c(x-1)2=ax+2a+bx2+bx-2b+cx2-2cx+c =(b+c)x2+a+b-2c)x+2a-2b+c. Identifier : (b+c)x2+(a+b-2c)x+2a-2b+c =3x2-2x. b+c=3 ; a+b-2c =-2 ; 2a-2b+c=0. éliminer b : a+3-3c=-2 ; 2a-6+3c=0. éliminer c : a =-5+3c ; -10+6c-6+3c=0 , c = 9c = 16 , c = 16/9. par suite a = 3/9 et b = 11/9. 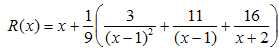En déduire la décomposition en éléments simples de la dérivée de R(x). Dérivée de x : 1. Dérivée de (x-1)-2 : -2(x-1)-3. Dérivée de (x-1)-1 : -(x-1)-2. Dérivée de (x+2)-1 : -(x+2)-2. . 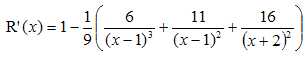Exemple 2. Décomposer en éléments simples la fraction rationnelle :  Factoriser le dénominateur : -1 est une racine évidente : x4+x3+x+1 = (x+1)(ax3+bx2+cx+d) = ax4+bx3+cx2+dx+ax3+bx2+cx+d = ax4+(a+b)x3+(b+c)x2+(c+d)x +d. Identifier : a=1 ; d=1 ; a+b=1 soit b = 0 ; b+c=0 soit c = 0. x4+x3+x+1 =(x+1)(x3+1). -1 est une racine évidente : x4+x3+x+1 =(x+1)2(x2+ex+1) =x4+ex3+x2+2x3+2ex2+2x+x2+ex+1 =x4+(e+2)x3+2(1+e)x2+(e+2)x+1. d'où e = -1 et x4+x3+x+1 =(x+1)2(x2-x+1). (x2-x+1) ne possède pas de racines réelles, le discriminant b2-4ac = (-1)2-4*1*1 est négatif. Réduire au même dénominateur ; le numérateur vaut : N = a(x2-x+1)+b(x+1)(x2-x+1)+(cx+d) (x+1)2. Développer : ax2-ax+a+bx3-bx2+bx+bx2-bx+b +cx3+dx2+2cx2+2dx+cx+d=(b+c)x3+(a+d+2c)x2+(2d+c-a)x+a+b+d. Identifier : (b+c)x3+(a+d+2c)x2+(2d+c-a)x+a+b+d =-3x3-2x2+1. b+c=-3 ; a+d+2c=-2 ; 2d+c-a=0 ; a+b+d=1. éliminer b : b = -3-c ;  a+d+2c=-2 soit a+c+d=1 ; 2d+c-a=0 ;  a+d-c=4. éliminer c : c = a-2d ; 3a-3d=-2 ;  3d=4 ; d = 4/3 d'où a =2,3 ;  c = 2/3-8/3 = -2 ; b =-1 ; . .

menu