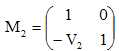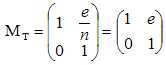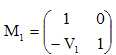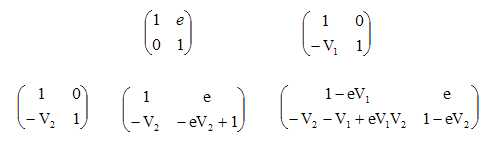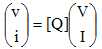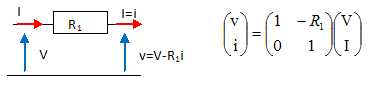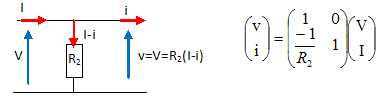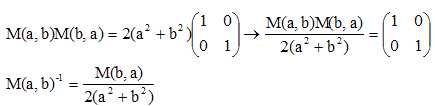Applications des matrices en optique et électricité.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
Réalisation d’un téléobjectif par association de deux lentilles distantes de e.
Afin de raccourcir les téléobjectifs, en particulier les plus
puissants, on peut réaliser un autre montage en associant deux
lentilles distantes d’une distance e : une lentille convergente L1 de centre O1 et de focale f’1 et une lentille divergente L2 de centre O2 et de focale f’2. On prendra pour les applications numériques : f’1 = 50 mm, f’2 = -25 mm et e = O1O2
= 31 mm. On note P l’intersection du plan de la pellicule avec l’axe
optique et F’ l’image par le téléobjectif d’un point à l’infini sur
l’axe optique.
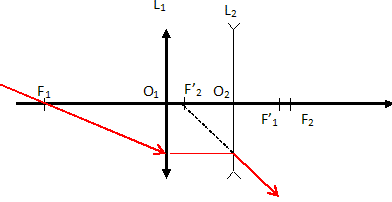
Déterminer littéralement la position de F’en fonction de f ’1, f ’2 et e.
Matrice de transfert du dioptre L2 de vergence V2 : 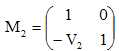
Marice de translation O1O2=e, milieu d'indice n=1 :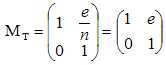
Matrice de transfert du dioptre L1 de vergence V1 :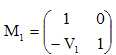
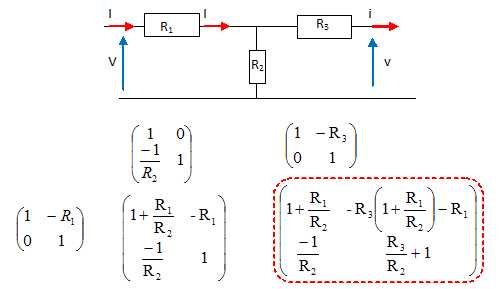
Matrice de transfert du doublet : M=M2MTM1.
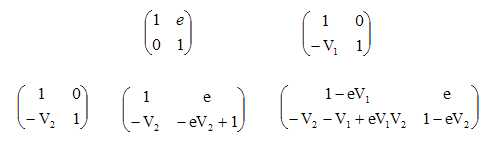
vergence du doublet : V = V1+V2-eV1V2.
1/F' = 1/f '1 + 1/f '2 - e /(f '1f '2).
|
|
|
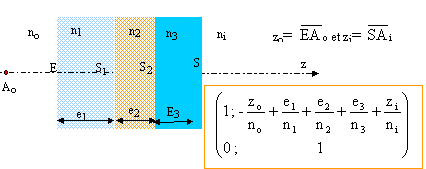
Succession de
dioptres plans :
L'image d'un objet Ao
situé au point de coordonnée zo et
située au point Ai de coordonné
zi telle que :
-zo / no + e1 /
n1+ e2 / n2+ e3
/ n3+ zi / ni =0
Calculer la hauteur de l'eau dans
un verre dont le fond est épais sachant que
:
- l'objet est placé contre
le verre
- l'image définitive se
trouvant sur le dioptre plan verre- eau.
indice du verre n1 = 1,5
; de l'eau n2 =1,33.
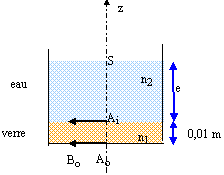
-zo / no + e1 /
n1+ e2 / n2+ zi
/ ni =0
0 +0,01 / 1,5 + e / 1,33 +
zi = 0
zi est la mesure
algébrique de SAi soit -e
0,01 / 1,5 + e /1,33 -e = 0 ; e =
2,66
cm.
|
.
Démontrer
que M(a,b) est inversible lorsque a ou b est non nul. En déduire alors
sont inverse en fonction de M(b,a).
Si le déderminant de M(a,b) est différent de zéro, alors Mm(a,b)
est régulière ou inversible.
D
= (a+b)2-(b-a)(a-b) =(a+b)2+(a-b)2
=a2+b2+2ab+a2+b2-2ab
=2(a2+b2).
D
diffère de zéro si a ou b est non nul.
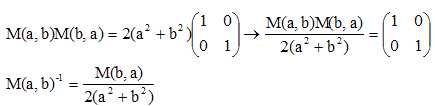
|
.
|