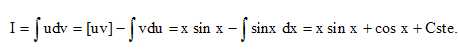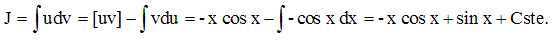Mathématiques, étude de fonction et calcul
intégral, concours ingénieur territorial.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
Etude
d'une
fonction. ( sujet 2011)
Soit la fonction définie sur [0 , + p]
par f(x) = e -x sin x.
On désigne par C la courbe représentative de f dans un repère
orthogonal (O, i, j).
Vérifier
que pour tout réel x de [0 , +p], on a cos
x-sin x = 2½ sin ( 0,25p-x).
cos x = sin ( ½ p-x)
; sin a -sin b = 2 cos (( a+b)/2) sin ((a-b)/2).
A = sin ( ½p-x) -sinx avec a+b = ½ p et a-b =½ p-2x ;
A = 2 cos 0,25 p
sin (0,25 p-x)
=2*0,707 sin
(0,25p-x)
= 2½sin (0,25p-x).
Etudier
les variations de f sur [0 , +p], et
dresser le tableau de variation.
On pose u = e-x et v = sin x ; u' = -e-x
; v' = cos x.
Dérivée d'un produit : f '(x) = u' v + v' u
= -e-x sin x +e-x cos x =
e-x ( cos x - sin x ).
f '(x) = 2½ e-x sin (0,25p-x).
2½ e-x est toujours
positif ; sin (0,25p-x) est nul pour
x = 0,25p sur [0 , +p].
sin (0,25p-x) est négatif
si x > 0,25p ; sin (0,25p-x) est positif
si x < 0,25p .

Ecrire un
dévelopement limité de f au voisinage de zéro.
Au voisinage de zéro : sin x = x-x3/6
+ x3e(x)
; e-x = 1 -x+½x2-x3/6
+ x3e(x).
f(x)=e-x sin x = ( x-x3/6
+ x3e(x)) (1 -x+½x2-x3/6
+ x3e(x)).
Développer en se limitant à l'ordre 3 :
f(x) = x-x3/6 -x2
+½x3+ x3e(x) = x -x2
+x3/3+ x3e(x).
En déduire
une
équation de la tangente T à la courbe C au point d'abscisse x=0.
y = x.
Etudier la
position
relative de T et C au voisinage du point d'abscisse 0, pour x positif.
Au voisinage de zéro, f(x)-y =-x2 +x3/3 avec x positif.
f(x)-y
est négatif ; f(x) < y : la
tangente est située au dessus de la courbe C.
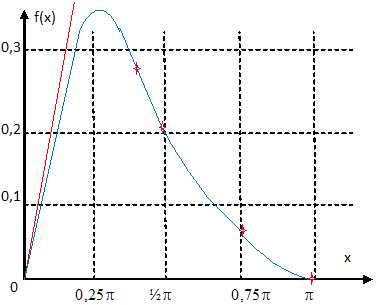
Construire
la tangente T et la courbe C.
Echelles : 5 cm en abscisses et 10cm en ordonnées.
|
|
|
En utilisant le fait que f est une solution de l'équation diférentielle
(E), déterminer
une primitive F de f sur [0; p].
On cherche une primitive de la forme F =A e-x
cos ( x+b) avec A et b des constantes réelles.
Dériver : f = -Ae-x cos ( x+b)-Ae-x sin ( x+b)
= -Ae-x(
cos(x+b)+sin(x+b)).
Or cos a + sin a = 2½ sin (a+0,25 p).
f = -Ae-x 2½ sin
(x+b+0,25 p)
= e-x sin x.
On identifie A =-1/2½ et b = -0,25 p ; F = -1/2½e-xcos ( x-0,25 p).
En
déduire l'aire en cm2 du
domaine délimité par la courbe C et l'axe des abscisses.
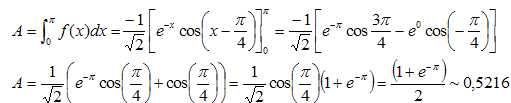
A =
0,5216 unité d'aire.
1 unité d'aire = 5*10 = 50 cm2 ; A =0,5216*50
=26,08 cm2 = 2608 mm2.
|
.
|
|
Sujet
2009.
Le
plan est rapporté à un repère orthogonal d'origine O ; unité 3 cm sur
chaque axe. On considère la courbe paramétrée C définie sur [0 ;
½p]
par :
M(t)
: x(t) = sin2t =0,5(1-cos 2t) ; y(t) = 4 sin t
cos t = 2 sin 2t.
Calculer
les coordonnées du point M(½p-t)
puis celles du milieu N(t) du segment [M(t)M(½p-t)].
En
déduire que C est symétrique par rapport à une droite (D) qu'on
précisera. En déduire un intervalle d'étude d'origine O.
M(½p-t) : x(½p-t)
= sin2(½p-t)
=
cos2t = 1-sin2t
;
remarque : sin(½p-t)
=cos t.
y(½p-t)
= 2 sin (2(½p-t)) =2 sin(p-2t) = 2 sin 2t.
N(t) : x(t) = 0,5(sin2t
+1-sin2t)
= 0,5 ; y(t) = 0,5(2 sin 2t + 2 sint 2t = 2 sin 2t.
La
courbe est symétrique par rapport à la droite d'équation x = 0,5.
L'intervalle d'étude est ramené à [0 ; 0,25 p].
Calculer
les dérivées des fonctions x(t) et y(t). Préciser
les signes de x'(t) et y'(t) sur l'intervalle d'étude.
On pose u = sin t ; u' = cos t ; x(t) = u2 ; u'
= 2 u u' : x'(t) =2 sin t cos t = sin 2t. x'(t) est positive
sur [0 ; 0,25 p].
y' = 2*2cos 2t = 4 cos 2t. y'(t) est positive sur
[0 ; 0,25 p].
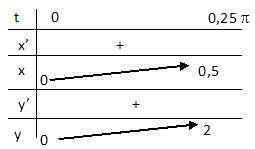
Former le
tableau de variation de x(t) et y(t) sur l'intervalle d'étude .
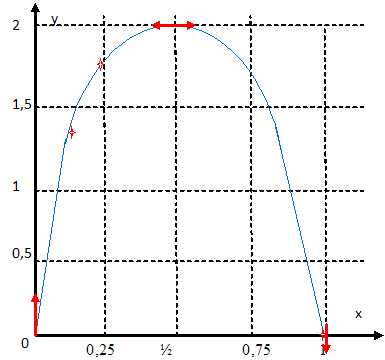
Tracer la
courbe C ; préciser la tangente en chacun des points O, A=M(0,25p) et B =M(½p).
La pente de la tangente à la courbe y(x) est donnée par y'/x'.
En O et en B : pente infinie, tangente verticale ; en A : pente nulle,
tangente horizontale.
On note (D) la partie du plan limitée par (C) et l'axe des abscisses. Calculer
en cm2 l'aire de
(D).
Déterminer
l'équation de (C) sous la forme y = f(x). On exprimera
sint et cost en fonction de x(t).
y(t)
= 4 sin t cos t ; x(t)
= sin2t . y2 =
16 sin2t cos2t.
cos2 t = 1-sin2t
=1-x ; y2 = 16 x (1-x)
; y= 4x½(1-x)½= 4
[x(1-x)]½.
On pose u = sin2 t alors 1-u = 1-sin2
t = cos2 t et u' = 2 sin t cos t = sin (2t).
y (u) = 4sin t cos t =2 sin 2t ; y du = 2 sin2(2t)
dt = (1-cos(4t) dt.
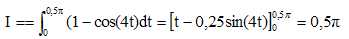 unités d'aire. unités d'aire.
|
Calcul
intégral. ( sujet 2008)
Soient f et g les fonctions définies sur R par : f(x) = x cos x et g(x)
= x sin x.
Calculer
la primitive F de la fonction f qui vérifie F(0) =1.
Intégration par parties en posant u= x et v' = cos x ; u' = 1 et v =
sin x.
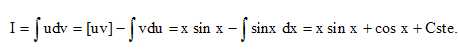
F(0) = 1+Cste = 1, la constante d'intégration est nulle et F= x sin x+
cos x.
Calculer
la primitive G de la fonction g qui vérifie G(0) =0.
Intégration
par parties en posant u= x et v' = sin x ; u' = 1 et v = -cos x.
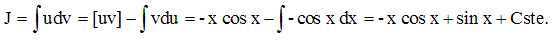
G(0) =cste = 0, la constante d'intégration est
nulle et G= -x cos x+ sin x.
Sujet 2006.
Soit la fonction f définie sur R par f(x) =(x-arctan x)/x2 si x différent de zéro et f(0) = 0.
Etudier la parité de f et conclure.
f(-x) = (-x-arctan(-x)) / (-x)2=(-x+arctan x) / x2 =-f(x). La fonction est impaire.
Sa courbe représentative C est symétrique par rapport à l'origine O du repère orthonormé.
Quelle est la limite de x quand x tend vers plus l'infini ?
f(x) = 1/x -arctan x / x2.
Quand x tend vers plus l'infini : 1/x tend vers zéro ; arctan x tend vers ½p et arctan x / x2 tend vers zéro.
f(x) tend vers zéro quand x tend vers plus l'infini.
La droite d'équation y=0 est une asymptote.
Calculer le développement limité à l'ordre 3 au voisinage de zéro de la fonction g(x) = arctan x.
On pourra utiliser la formule de Taylor-Young
g(x) = g(0) +x g'(0) +½x2g"(0) +x3/3! g"'(0)+x3e(x).
g(0) = 0 ; g'(x) = 1/(1+x2) et g'(0) = 1 ; g"(x) = -1(2x)/(1+x2)2 et g"0) = 0.
On pose u = -2x et v = (1+x2)2; u' = -2 et v' = 4x(1+x2).
Dérivée d'un quotient : g'''(x) =(u'v-v'u)/v2 =[-2(1+x2)2 +8x2(1+x2)] / (1+x2)4=[-2(1+x2) +8x2] / (1+x2)3 ; g'''(0) = -2.
g(x) =x-x3/3 +x3e(x).
Déduire du résultat précédent que f est dérivable pour x=0 et donner la valeur de f '0).
Développement limité de f(x) au voisinage de zéro ;
f(x) =[ x - x +x3/3 +x3e(x)] / x2 = x/3+x e(x).
Les deux propriétés suivantes sont équivalentes :
f admet un développement limité en x0 et f est dérivable en x0.
Au voisinage de zéro ; f '(x) = x/3 et f '(0) = 0.
En déduire sans nouveau calcul que f est continue pour x=0.
Toute fonction dérivable en un point est continue en ce point.
|
Sujet 2004.
Dans le plan rapporté à un repère orthogonal, on considère la courbe paramétrée C définie par :
M(t) : x(t) =3 cos t -2 cos3 t ; y(t) = 2 sin3 t.
Montrer que C est symétrique par rapport à l'axe des abscisses.
La fonction cosinus est paire : x(t) = x(-t) ; la fonction sinus est impaire : y(-t )=2 sin3 (-t) =-2 sin3 t = -y(t).
En utilisant M(p-t) montrer que C est symétrique par rapport à l'axe des ordonnées.
Rappel : sin t = sin (p-t) et cos (p-t) = - cos t.
x(p-t) =3 cos (p-t) -2 cos3 (p-t) = -3 cos t +2cos3 t = -x(t).
y(p-t) = 2 sin3 (p-t) = 2 sin3 t = y(t).
Montrer que l'on obtient toute la courbe C en faisant varier t dans un intervalle d'amplitude 2p.
cos3t = cos t cos2t = cos t (1+cos 2t ) /2 =½ cos t + ½cos t cos 2t .
Or : cos t cos 2t =½(cos (t+2t) + cos ( t-2t)) = ½( cos 3t +cos t )
cos3t =½ cos t +0,25( cos 3t +cos t ).
La période de cos t est égale à 2p et celle de cos 3t est égale à 2p/3.
De même sin3t = sin t sin2t = sin t (1-cos 2t ) /2 =½ sin t - ½sin t cos 2t .
Or : sin t cos 2t =½(sin (t+2t )- sin ( t-2t)) = ½( sin 3t +sin t )
sin3t =½ sin t +0,25( sin 3t +sin t ).
La période de sin t est égale à 2p et celle de sin 3t est égale à 2p/3.
Calculer les dérivées x'(t) et y'(t), puis déterminer leurs signes pour t appartenant à [0 ; ½p].
x'(t) = -3 sin t-2*3(-sin t)cos2t = 3 sin t ( -1+2 cos2t)= 3 sint (-1+1+cos 2t) =3 sin t cos 2t.
Sur l'intervalle considéré, sin t >0 :-1+2 cos2t =0 si t = 0,25 p ; -1+2 cos2t >0 si t est compris entre 0 et 0,25 p ; -1+2 cos2t <0 si t est compris entre 0,25 p et 0,5 p ;
x'(t) est positive sur [0 ; 0,25 p[ et négative sur ]0,25p ; 0,5 p].
y't) =6 cos t sin2 t ; cos (t) est positive sur l'intervalle considéré.
Former le tableau de variation de x(t) et y(t).
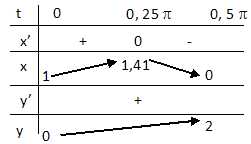
On désigne par C1 la partie de C correspondant à t appartenant à [0 ; 0,5 p]
Préciser la tangente en M(0) et les points où la tangente à C1 est parallèle aux axes de coordonnées.
y' / x' = 6 cos t sin2 t / (3 sint cos 2t)) =2 sin t cos t / cos 2t = tan 2t ; en M(0) : y'/x' = 0, tangente horizontale.
En M(0,25 p) : y'/x' tend vers l'infini, la tangente est verticale.
Comment déduit-on C de C1 ?
Symétrie par rapport à l'axe des abscisses et symétrie par raport à l'axe des ordonnées.
Construire C.
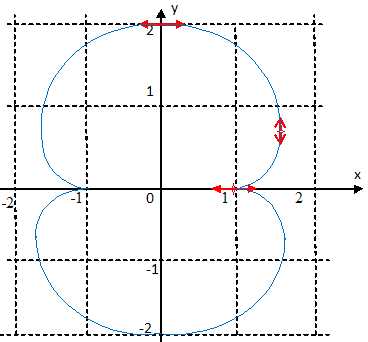
Calculer l'aire S de la partie du plan limitée par C.
L'aire S est égale à 4 fois l'aire limitée par C1 et les axes.
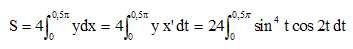
sin4t =0,25(1-cos 2t)2 =0,25(1-2 cos 2t+cos2 2t) =0,25(1-2 cos 2t +0,5(1+cos 4t) = 0,25(1,5 -2 cos 2t +0,5 cos 4t)
sin4t cos 2t = 0,25(1,5 -2 cos 2t +0,5 cos 4t) cos 2t = 0,25(1,5 cos 2t -2 cos2 2t +0,5 cos 2t cos 4t) ;
0,25(1,5 cos 2t-(1+cos 4t) +0,5*0,5( cos 2t +cos 6t)) = 0,25( -1 +1,75 cos 2t -cos 4t + 0,25 cos 6t).
Intégrer entre 0 et ½p : 0,25[-t +1,75/2 sin 2t -0,25 sin 4t +0,25/6 sin 6t]00,5p =0,25(-0,5p).
aire S = 24 *0,25*0,5p = 3 p unités d'aire.
|


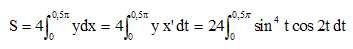


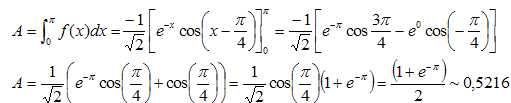


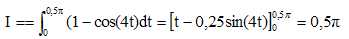 unités d'aire.
unités d'aire.