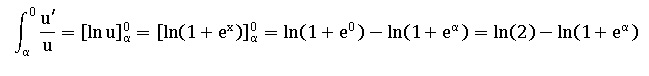Mathématiques,
Physique,
Concours TSPEI 2017.
Technicien supérieur principal de l'économie et de l'industrie.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Etude
d'une fonction.
Soit f la fonction définie dans R par : f(x) = ex
/ (1+ex).
1. Calculer f(0).
Déterminer les limites de f en -oo et +oo.
f(0) = 1 / (1+1) = 1 / 2 = 0,5.
Quand x tend vers moins l'infini ex tend vers zéro et fx()
tend vers zéro.
f(x) = 1 / (1 +e-x) ;
Quand x tend vers plus l'infini, f(x) tend vers 1.
2. Calculer la dérivée de f. En déduire le
tableau de variations.
On pose u = ex et v = 1+ex ; u' =ex ;
v' = ex.
f ' = (u'v -c ' u) / v2 =[ ex(1+ex) -e2x)
/ (1+ex)2.
f ' =ex/ (1+ex)2.
ex étant positif, la dérivée est positive et f (x) est
strictement croissante.
3. Montrer que le point I(0 ; 0,5)
est centre de symétrie de la courbe.
Montrons que le symétrique par rapport à I de tout point de la courbe
appartient à la courb, soit :
f(xI-x) +f(xI+x) = 2yI.
f(0-x) + f(0+x) = e-x / (1+e-x) +
ex / (1+ex) = [e-x(1+ex) +ex(1+e-x)]
/ [(1+ex)(1+e-x)].
f(0-x) + f(0+x) = ( e-x+1+ex+1) / ( e-x+1+ex+1) = 1 = 2 yI.
4. Ecrire une équation de la
tangente à la courbe au point I.
Coefficient directeur de la tangente à la courbe en I : f '(0) = 1 /
(1+1)2 = 0,25.
La tangente passe en I (0 ; 0,5) : 0,5 = 0,25 *0 +b soit b = 0,5.
y = 0,25 x +0,5.
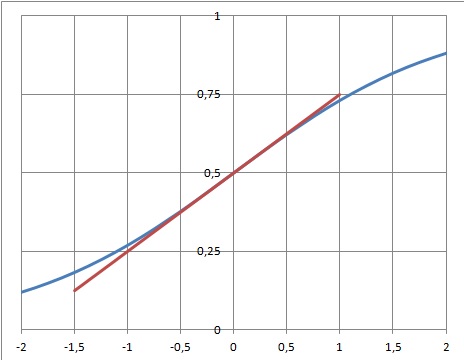
5. Construire la courbe et la
tangente en I.
6. Soit a <0. Déterminer l'aire
comprise entre la courbe, l'axe des abscisses et les droites d'équation
x=0 et x = a.
Déterminer la limite de cette aire quand a tend vers moins l'infini.
On pose u = 1 +ex ; u' = ex.
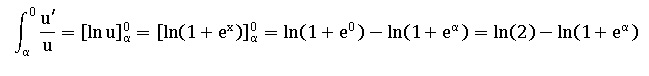
Quand a tend vers
moins l'infini, ea
tend vers zéro. L'aire tend vers ln (2).
|
|
.
.
|
|
|
Second
problème.
Une
entreprise a embauché 10 opérateurs, 6 hommes et 4 femmes. Elle veut
constituer une équipe comprenant 6 opérateurs qui travailleront dans la
nouvelle unité de production. L'entreprise choisit au hasard les 6
membres de l'équipe parmi les 10 embauchés. On supposera que les choix
d'équipes sont équiprobables.
1. Déterminer le
nombre d'équipes possibles.
Aucune femme et 6 hommes ; 1 femme et 5 hommes ; 2 femmes et 4 hommes ;
3 femmes et 3 hommes ; 4 femmes et 2 hommes.
Nombre d'équipes possibles : tirages de 6 personnes parmi 10, sans
ordre.
C106 = 10 x 9 x 8 x7 x 6 x
5 / (2 x 3 x 4 x 5 x 6) = 210.
2. Quelle est la probabilité
d'avoir une équipe formée de 6 hommes ? Composée de 3 hommes et de 3
femmes ?
Une seule possibilité de former une équipe de 6 hommes. Sa probabilité
est égale à 1 / 1260.
On choisit 3 hommes parmi 6 et 3 femmes parmi 4 :
C63 x C43
= 6 x5 x4 / (2 x3) x 4 x 3 x 2 / (2 x 3)= 20 x 4 = 80 possibilités.
Probabilité de former une équipe de trois hommes et 3 femmes : 80 / (90
x14) = 4 / 72.
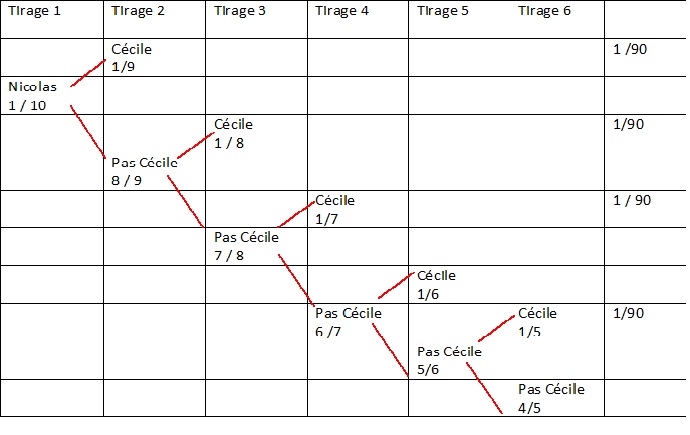
3.
Deux opérateurs, Cécile et Nicolas, désirent travailler ensemble dans
la nouvelle unité de production. Quelle est la probabilité de voir leur
voeux se réaliser ?.
4. Lors du
recrutement, les 10 opérateurs ont été classés par ordre de mérite : du
rang 1 au rang 10. On choisit au hasard un opérateur parmi les 10. Soit
X la variable aléatoire égale au rang de l'opérateur choisi. Déterminer
la loi de X et son espérance E(X).
Loi uniforme discrète d'espérance (1+10) / 2 = 5,5.
|
|
|
|
Acummulateur NiMH.
Cet accumulateur est chargé pendant Dt = 6 h. La tension à ses
bornes est U = 1,40 V et l'intensité du courant qui la traverse est I =
110 mA.
1. Calculer la
puissance électrique Pe et l'énergie électrique We
reçue par cet accumulateur.
Pe = UI = 1,40 x0,110 = 0,154 W.
We =Pe Dt
=0,154 x 6 x3600=3326,4 ~3,33 103 J.
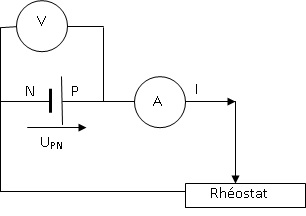
Une fois chargé, cet accumulateur peut servir de générateur. On mesure
la tension U aux bornes de l'accumulateur en fonction de l'intensité I
qui le traverse.
2. Compléter le
schéma en indiquant la tension UPN, le sens du courant et
les appareils de mesures nécessaires.
UPN(V)
|
1,10
|
1,06
|
1,03
|
0,99
|
0,95
|
0,91
|
0,88
|
0,84
|
I(mA)
|
100
|
125
|
150
|
175
|
200
|
225
|
250
|
275
|
3. Tracer UPN
= f(I).
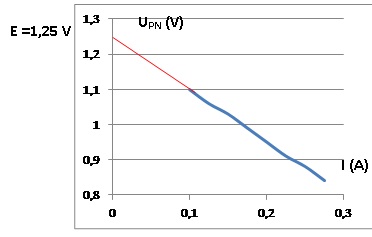
4. En déduire la
fem E et la résistance interne r de cet accumulateur.
E = 1,25 V, ordonnée à l'origine.
r = valeur absolue de la pente de la droite : r = (1,1-0,88) /
(0,25-0,1) ~1,5 ohms.
5. Pour UPN
= 1,00 V, calculer la puissance dissipée par effet Joule.
UPN = 1,25 -1,5 I ; I = (1,25-1) / 1,5 ~0,167 A.
Pjoule = r I2 = 1,5 x 0,1672
~0,042 J.
Réacteur nucléaire.
L'uranium enrichi à 3,7 % subit la réaction de fission :
23592U + 10n
---> 94xSr + 13954Xe +
y 10n.
1.
Déterminer x et y en justifiant.
Conservation du nombre de nucléons : 235+1 = 94 + 139 + y ; y = 3.
Conservation de la charge : 92 = x +54 ; x = 38.
23592U + 10n
---> 9438Sr + 13954Xe
+ 3 10n.
2. Calculer en MeV
l'énergie libérée par la fission d'un noyau d'uranium.
|
noyau
|
23592U
|
9438Sr
|
13954Xe
|
10n
|
|
masse (u)
|
234,993 45
|
93,894 51
|
138,889 17
|
1,00866
|
1 MeV = 1,602 10-13 J ; c
= 2,998 108 m/s ; 1 u = 1,66054 10-27 kg ; 1 tep
= 42 GJ ; NA = 6,02 1023 mol-1.
Variation de masse Dm =2 m(10n)
+ m(113954Xe) + m( 9438Sr)
- m(23592U)
Dm = 2*1,00866 +138,889 17
+93,894 51-234,99345= -0,19245 u
-0,19245*1,66054 10-27 = -3,195709 10-28 kg.
Cette diminution de masse s'acompagne de la libération d'énergie dans
le milieu extérieur ( ce que traduit le signe négatif) :
Dm c2 = -3,195709 10-28
*(2,998 108)2 = -2,8723 10-11 J .
-2,8723 10-11 / 1,6 10-13
= 1,7951 102
MeV.
3. Estimer
l'énergie libérée par la fission d'une masse m = 1,0 g d'uranium
enrichi.
Nombre de noyaux d'uranium 235 : 0,037 / M(235U) NA
=0,037 / 235 x 6,02 1023 ~9,48 1019.
QC= 2,8723 10-11 x 9,48 1019 ~2,72 109
J.
4. L'eau du circuit
secondaie sort à l'état de vapeur au contact de la source chaude à TC
= 563 K, entraîne les turbines, se refroidit puis se condense au
contact de la source froide à TF = 308 K.
Enoncer le premier principe de la thermodynamique. En déduire une
relation entre Qc, transfert thermique échangé avec l'eau à
la source chaude, QF transfert thermique échangé à la source
froide et W le travail échangé au cours du cycle.
Dans toute transformation, il y a conservation de l'énergie.
La variation d'énergie interne du fluide est nulle au
cours du cycle. QF + QC +
W=0.
Enoncer le second principe de la thermodynamique et en déduire une
relation entre Qc, QF, TC et TF.
Toute transformation d'un système thermodynamique s'efectue avec
augmentation de l'entropie globale.
La variation d'entropie du fluide est nulle au cours
du cycle effectué réversiblement. QF /TF +
QC /TC=0.
Définir et exprimer le
rendement r de la transformation d’énergie thermique en travail
mécanique.
Le rendement est égal à
la valeur absolue du travail fourni à la turbine divisé par
l'énergie reçue de la source chaude.
r = |W| / QC.
W
= -(QF + QC )
; |W|= QC + QF ; r
= (QC + QF ) / QC =1 +QF / QC.
or : QF /TF +
QC /TC=0 soit : QF / QC = -TF /
TC.
r = 1-TF / TC =
1-308 / 563 ~0,45 ( 45 %).
|
|
Mesure
d'un débit..
On insère dans une conduite un tube de venturi
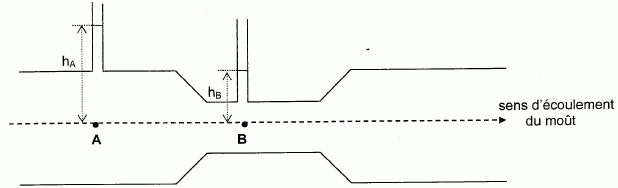
Le rapport des diamètres
est noté ß = DB / DA.
1. Définir le débit
volumique et montrer qu'il s'écrit Qv = S. v.
Ecrire la conservation du débit volumique entre les sections droites SA
et SB.
Le débit volumique est le
volume de fluide ( m3) qui traverse une section droite du
tube par unité de temps (s).
dV
( volume) = section * déplacement ; dV = S dx ; dx/dt est une vitesse
d'où dV/dt = S v.
Le débit volumique (m3 s-1) est
donc une section (m2) fois une vitesse (m s-1).
La conservation du débit volumique s'écrit : SA vA
= SB vB.
2. les points A et
b étant à la même altitude, le théorème de Bernoulli s'écrit :
PA +½rv2A
=PB +½rv2B
.
Comparer en justifiant vA et vB ainsi que PA
et PB.
SA > SB ; de plus le débit volumique est
constant, donc vA < vB.
Le théorème de Bernoulli conduit alors à PA > PB.
3. Exprimer vB
en fonction de DP
= PA-PB, r,
et ß.
PA -PB +½rv2A =½rv2B .
2 DP / r +v2A
=v2B
.
Or SA vA = SB vB ; pD2A vA
/ 4 = pD2B
vB / 4 ; vA = ß2 vB.
2 DP / r +ß4v2B
=v2B
; 2 DP / r =v2B
(1-ß4).
v2B
=2 DP /( r (1-ß4)).
4. Montrer que le
tube de Venturi crée une dépression DP proportionnelle à Q2v.
Exprimer le coefficient de proportionnalité k en fonction de r, ß et de SB.
Qv =SB vB ; Q2v
=S2B v2B ; Q2v
=S2B 2 DP
/( r (1-ß4))
;
DP = r (1-ß4) Q2v
/(2S2B ) ; k = r (1-ß4)
/(2S2B ).
|
|