Mathématiques, physique,chimie, Concours TSPEI 2015.

Mathématiques, Physique, chimie, Concours TSPEI 2015.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

Exercice 1.
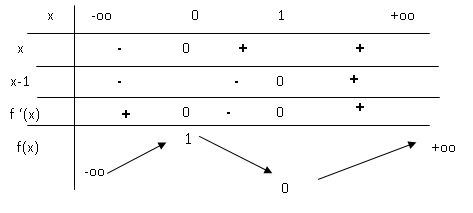
On considère la fonction définie sur R par : f(x) = 2x³-3x²+1.
1. Calculer f(0) et f(1). Déterminer les réels a, b, c tels que, pour tout x réel, on ait :
f(x) = (x-1)(ax²+bx+c).
f(0) = 1 ; f(1) =0.
(x-1)(ax²+bx+c)=ax³ +bx²+cx-ax²-bx-c.
Par identification a = 2 ; b-2 =-3 soit b = -1 ; c = -1.
f(x) = (x-1)(2x²-x-1).
2. En déduire l'ensemble des solution de f(x)=0.
x-1=0 soit x=1 ;
2x²-x-1 =0 ; D =(-1)² -4(-1)x2 = 9
Solutions : x₁ = (1+3)/4=1 et x₂ = (1-3)/4=-0,5.
3. Calculer la dérivée de la fonction f et en déduire le tableau de variations de f.
f '(x) = 6x²-6x = 6x(x-1).

Soit (X) la courbe représentative de f.
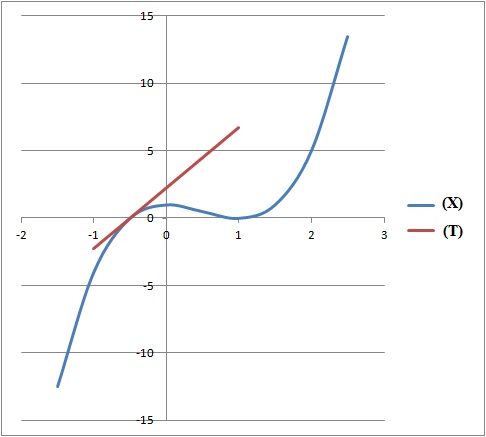
4. Déterminer une équation de la tangente (T) à la courne (X) au point d'abscisse x = -0,5.
f '(-0,5) = 4,5.
Equation de (T) : y = 4,5 x +b.
La tangente passe par le point de coordonnées ( -0,5 ; f(-0,5) = 0 ).
Par suite 0 = 4,5(-0,5) +b ; b = 2,25.
y = 4,5 x +2.25.
5. Construire (X) et (T).

6. On se propose d'installer une rampe d'accès en pente douce permettant à des chariots de franchir une marche.

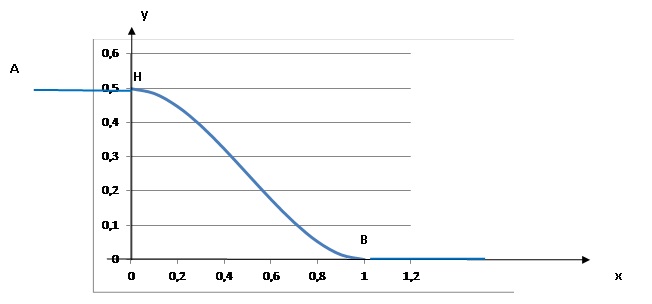
La courbe définie par le profil de la rampe doit être tangente en B à l'axe (Ox) et en H à la droite (AH). Déterminer les réels a, b, c tels que la courbe définie par le profil ait pour équation
y = ax³ +bx²+c.
y' = 3ax² +2bx.
En H, tangente horizontale d'équation y = 0,5.
En B, tangente horizontale d'équation y = 0.
Par suite y'(1) = 3a+2b =0. (1).
La courbe passe en H(0 ; 0,5) : 0,5 = c.
La courbe passe en B(1 ; 0) ; 0 = a +b +0,5 soit b = -a-0,5.
Repport dans (1) : 3a-2a-1=0 soit a = 1 et b = -1,5.
y = x³-1,5x²+0,5.

.
.

....

...
Exercice 2.
Un inspecteur est chargé de contrôler trois unités de production notées A, B et C. Chaque mois il effectue un seul contrôle dans une unité choisie au hasard parmi A, B et C. On admet que les choix sont équiprobables et indépendants. On considère une période de 6 mois.
Contrôles possibles au bout de 1 mois : A ; B ; C.
Contrôles possibles au bout de 2 mois : AA, AB, AC, BB, BC, CC.
Contrôles possibles au bout de 3 mois : AAA, AAB, AAC, ABC, BBB, ABB, BBC, CCC, ACC, BCC .
Contrôles possibles au bout de 4 mois : AAAA, AAAB, AAAC, AABB, AACC, AABC, ABCC, ABBB, ABBC, BBBB, BBBC, BBCC, CCCC, ACCC, BCCC.
Contrôles possibles au bout de 5 mois : AAAAA, AAAAB, AAAAC, AAABC, AAACC, AAABB, AABBB, AABBC, AABCC, AACCC, ABBBC, ABBCC, ABCCC, ABBBB, BBBBC, BBBCC, BBCCC, ACCCC, BCCCC, CCCCC, BBBBB.

Contrôles possibles au bout de 6 mois : AAAAAA, AAAAAB, AAAAAC, AAAABB, AAAABC, AAAACC, AAABBC, AAABCC, AAACCC, AAABBB, AABBBB, AABBBC, AABBCC, ABBBBC, AABCCC, AACCCC, ACCCCC, ABBBCC, ABBCCC, ABCCCC, ABBBBC, ABBBBB, BBBBBC,
BBBBCC, BBBCCC, BBCCCC, ACCCCC, BCCCCC, CCCCCC, BBBBBB.
1. Quelle est la probabilité que pendant cette période seule l'unité A soit contrôlée ?
probabilité que seule A soit contrôlée : 1 / 30..
2. Quelle est la probabilité que pendant cette période une seule unité soit contrôlée ?
3 cas favorables ( AAAAAA, BBBBBB, CCCCCC) sur 30.
Probabilité qu'une seule unité soit contrôlée : 3 / 30 = 1 / 10.
3. Quelle est la probabilité que pendant cette période au moins 2 unités soient contrôlée ?
2 ou trois unités doivent être contrôlées ; on exclut le cas du contrôle d'une seule unité.
Probabilité de contrôler au moins deux unités :1- 1 / 10 = 9 /10.
4. Quelle est la probabilité que pendant cette période les 3 unités soient contrôlée ?
10 cas favorables sur 30 ; probabilité que les 3 unités soient contrôlées : 1 /3.

On note X_A la variable aléatoire égale au nombre de contrôle éffectués au sein de l'unité A pendant la période considérée.
5. Quelle est la loi de X_A ? Donner son espérance. Interpréter le réssultat obtenu.

6 contrôles
5 contrôles
4 contrôles
3 contrôles
2 contrôles
1 contrôle
0 contrôle

1
2
3
4
6
8
6

Moyenne : (6+10+12+12+12+8+0)/30 = 2.
L'unité A est contrôlée en moyenne 2 fois tous les six mois
6. Quelle est la probabilité que 2 contrôles soient effectués au sein de A pendant la période considérée ?
6 / 30= 1 /5.

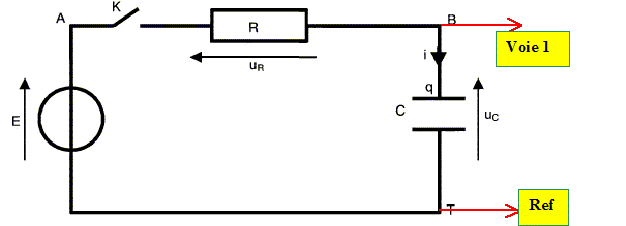
Stockage de l'énergie .
Un circuit électrique comprend, en série, un générateur idéal de tension de fem E = 12,0 V, un conducteur ohmique de résistance R, un condensateur de capacité C = 120 µF et un interrupteur.
Le condensateur est initialement déchargé et à la date t=0, on ferme l'interrupteur. On note q la charge de l'armature du condensateur qui se charge positivement.
1. Représenter par des flèches les tension u_c aux bornes du condensateur et u_R aux bornes du conducteur ohmique.

2. Donner l'expression de u_R en fonction de i.
u_R = Ri..
3. Donner l'expression de i en fonction de la charge q.
i = dq/dt.
4. Donner la relation liant q et u_c
q = Cu_C.
5. En déduire l'expression de i en fonction de C et u_C.
i = Cdu_C /dt.
6. En appliquant l'additivité des tensions, établir une relation entre E, u_R et u_C.
E = u_R + u_C.
7. Etablir l'équation différentielle à laquelle obeit u_C.
E =RC du_C/dt + u_C.
8. Résoudre cette équation.
Solution générale de l'équation sans second membre : u_C =A exp(-t / (RC)), avec A une constante.
Solution particulière de cette équation ( condensateur chargé) : u_C=E
Solution générale : u_C = E + A exp(-t/(RC)).
A t=0, u_C = 0 , d'où A = -E.
u_C = E(1-exp(-t/(RC)).
9a. Vérifier que t = RC est homogène à un temps.
R résistance soit tension / intensité ; C capacité soit charge / tension d'où on déduit : RC charge / intensité.
or une charge est une intensité fois un temps ; par suite RC a la dimension d'un temps
9b. Déterminer graphiquement t. En déduire la valeur de R.

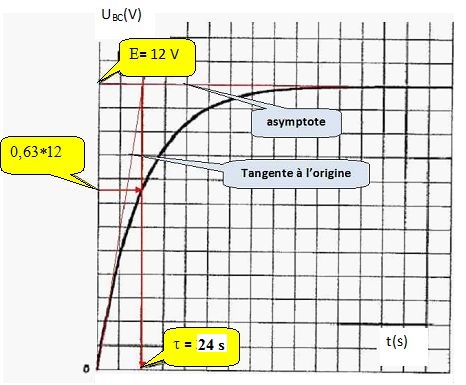
24 =120 10^-6 R ; R =24 / (120 10^-6) =2,00 10⁵ ohms.

Satellites.
1. Rappeler la loi de gravitation universelle.
Deux corps A et B de masses respectives m_A et m_B séparés d'une distance d exercent l'un sur l'autre des forces opposées attractives, importantes dans l'infiniment grand, négligeables dans l'infiniment petit. Ces forces sont proportionnelles aux masses et inversement proportionnelles au carré de la distance d.
Satellite en orbite circulaire.
Un satellite de la terre ( masse M et rayon R), de masse m est en orbite circulaire à l'altitude h = 300 km au-dessus de la terre.
2. Applique la seconde loi de Newton au satellite et montrer qie son mouvement est uniforme.
Le satellite est soumis à la seule force de gravitation centripète exercée par la planète

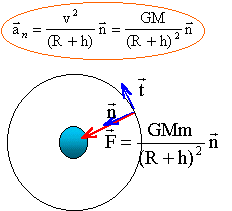
M : masse (kg) de la planète ; m : masse du satellite (kg) ; R (m) rayon planète ; h (m) altitude depuis le sol.
La force de gravitation est toujours perpendiculaire à la vitesse ; cette force ne travaillant pas, elle ne modifie pas la valeur de la vitesse : le mouvement est donc uniforme.
3. Déterminer l'expression de la vitesse en fonction de r = R+h, G et M.
Suivant l'axe n la seconde loi de Newton s'écrit : GMm /(R+h)² = m a_N=mv²/ (R+h)

d'où la valeur de la vitesse (m/s): v² =GM / (R+h) =GM / r. indépendante de la masse du satellite

4. Les satellitse de type SPOT évoluent sur des orbites circulaires d'altitude 830 km environ. Leur vitesse est-elle plus grande, plus petite ou égale à celle du satellite précédent ? Justifier
La vitesse diminue quand r= R+h augmente. SPOT a une vitesse inférieure à celle du satellite étudié ici
5. Exprimer la période du satellite en fonction de G, R, h et M.
Le satellite décrit la circonférence 2p(R+h) à la vitesse v en T seconde.
2p(R+h) = vT ;
élever au carré : 4p²(R+h)² = v² T² =GM /(R+h) T².
T =2p/ (GM)^½ (R+h)^1,5.
6. Montrer que la troisième loi de Kepler est vérifiée.
T²= 4p²(R+h)³ / (GM).
Le carré de la période est proportionnel au cube du rayon de l'orbite.
7. Préciser ce qu'est un satellite géostationnaire. Le satellite étudié est-il géostationnaire ?
Un satellite géostationnaire tourne dans le plan équatorial, dans le même sens que la terre, avec la même vitesse angulaire que la terre. Son altitude est proche de 36000 km.
Le satellite étudié n'est pas géostationnaire.

Fission nucléaire.
1. Donner la définition de la fission nucléaire.
Fission nucléaire spontanée : le noyau se désintègre en plusieurs fragments sans absorption préalable d'un corpuscule ( neutron par exemple).
Fission nucléaire induite : un noyau lourd capture un neutron puis se désintègre en plusieurs fragments.

2. Des réactions de fission sont induites par la capture d'un neutron et s'écrivent : ²³⁵₉₂U + ¹₀n ---> ⁹⁴_ZSr + ^A₅₄Xe + x ¹₀n

Quel phénomène se produit si x >2 ?
La réaction produit plus de neutrons qu'elle n'en consomme. Un réaction en chaine se produit

3. Pour x = 3, déterminer A et Z.
Conservation du nombre de nucléons :235+1=94+A+3 ; A =139.
Conservation de la charge : 92 = 54 +Z ; Z =38.
4a. Enoncer la relation d'équivalence masse - énergie.
Einstein postule que la masse est une des formes que peut prendre l'énergie. Un système de masse m possède lorsqu'il est au repos, une énergie: E = m.c²

E: énergie du système en joules (J) ; m: masse du système en kilogrammes (kg) ; c: vitesse de la lumière dans le vide (c=3,0.10⁸m.s^-1.

4 b.Exprimer en fonction des masses des particules et des noyaux intervenant dans l'équation précédente, la variation d'énergie de masse DE au cours de cette réaction nucléaire.

Variation de masse Dm =2 m(¹₀n) + m(¹¹³⁹₅₄Xe) + m( ⁹⁴₃₈Sr) - m(²³⁵₉₂U).
Dm = 2*1,0087 +138,888 2 +93,894 6-235,013 4= -0,2132 u.
-0,2132*1,660 10^-27 = -3,539 12 10^-28 kg.

Cette diminution de masse s'acompagne de la libération d'énergie dans le milieu extérieur ( ce que traduit le signe négatif) :

Dm c² = -3,539 12 10^-28 *(2,998 10⁸)² = -3,18096 10^-11 J ~ -3,181,0 10^-11 J.

-3,1810 10^-11 / 1,602 10^-13 = 1,985 6 10² MeV

Préparation industrielle du zinc.
Dans la nature, le zinc (Zn) se rencontre dans la blende, minerai constitué essentiellement de sulfure de zinc solide ZnS(s). Pour récupérer le métal zinc, dont la principale application est l'élaboration de l'acier zingué, la blende subit des transformations physico-chimiques.
La blende est transformée en calcine ( constituée principalement de ZnO) au moyen d'une opération appelé grillage. La calcine est alors traitée par hydrométallurgie pour obtenir le métal zinc quasiment pur.
Le grillage est effectué en chauffant fortement le sulfure de zinc en présence du dioxygène de l'air. L'équation de la réaction associée à la transformation est :

.... ZnS(s) + ....O₂(g) =....ZnO (s) +.... SO₂(g).

1.a Ajuster les nombres stoechiométriques.

2 ZnS(s) + 3O₂(g) = 2ZnO (s) +2 SO₂(g).
1.b. On grille une masse m = 1,00 t de sulfure de zinc. Déterminer la masse m₂ d'oxyde de zinc obtenue et le volume V de dioxygène nécessaire.
M(Zn) = 65,4 g /mol ; M(O = 16 g/mol ; M(S) = 32,1 g /mol. V_m = 25,0 L /mol.
Quantité de matière de sulfure de zinc : n = 1,00 10⁶ /(65,4 +32,1) =1,02564 10⁴ mol.
Quantité de matière d'oxyde de zinc :1,02564 10⁴ mol.
m₂ = 1,02564 10⁴. x(65,4 +16) =8,35 10⁵ g = 0,835 t.
Quantité de matière de dioxygène :1,5x1,02564 10⁴ = 1,5385 10⁴ mol.
V = 1,5385 10⁴ x25,0 =3,85 10⁵ L.

2. a. Ecrire l'équation de réduction de l'oxyde de zinc par le carbone. On obtient du monoxyde de carbone et du zinc.
ZnO(s) + C(s) ---> Zn(s) + CO(g).
2.b. Déterminer la masse m₃ de zinc obtenue.
Quantité de matière de ZnO = quantité de matière de zinc = 1,02564 10⁴ mol.
m₃ = 65,4 x1,02564 10⁴ ~6,71 10⁵ g.
3. . En réalité, le rendement de chaque opération successive ne dépasse jamais 80 %.
Quelle masse m₄ de zinc fabrique t-on par tonne de minerai ?
m₄ = 0,80 x0,80 m₃ = 0,80 x0,80 x6,71 10⁵ =4,30 10⁵ g = 0,430 kg.
4. Quelle masse m₅ de carbone est nécessaire à la préparation du zinc ?
Quantité de matière de carbone = quantité de matière de ZnO =1,02564 10⁴ mol.
Tenir compte du rendement de la première réaction : 1,02564 10⁴ x0,80 =8,205 10³ mol.
Masse de carbone : 12 x8,205 10³ ~9,85 10⁴ g.

Dosage des ions nitrate par spectrophotométrie.
La teneur en ion nitrate dans les eaux potables doit être inférieur à 50 mg / L.
Les ions nitrate sont réduits en ion nitrite puis traités par un réactif de diazotation pour obtenir un composé diazoïque de couleur rose dont on peut mesurer l'absorbance.
Une solution étalon d'ion nitrate de concentration massique C_m = 20,00 mg /L et de volume V = 200 mL subit le traitement ci-dessus et permet de préparer une série de fioles jaugées de 100,0 mL notées 0, 1, 2, 3, 4 selon les mélanges indiqués dans le tableau ci-dessous.

Fiole
0
1
2
3
4
X

Volume de solution réduite (mL)
0,00
2,00
4,00
6,00
8,00
5,00

Réactif de diazotation (mL)
1

Concentration massique ( mg/L)
0,00
2,00 /100 x20,00 =0,400
0,800
1,20
1,6
xxxxxx

Absorbance
0,00
0,251
0,524
0,782
1,031
0,657

On complète chacune des fioles jaugées à 100,0 mL avec de l'eau distillée. Après 15 minutes d'attente, une partie de la solution est transférée dans une cuve de longueur L=1,00 cm qui est placée dans le spectrophotomètre. Longueur d'onde de travail l = 540 nm.
1. Comment la longueur d'onde doit-elle est choisie pour cette mesure ?
Pour une meilleure précision, la longueur d'onde de travail doit correspondre au maximum d'absorption de la solution.
2. La solution étalon a été préparée à partir de nitrate de potassium KNO₃.
2.a. Déterminer la masse m de nitrate de potassium nécessaire pour préparer la solution étalon.
M(KNO₃) = 39,1 +14 +3x16 = 101,1 g/mol. M(NO₃^-) = 14+3x16=62 g/mol.
Quantité de matière d'ion nitrate : 20,00 / 62 mmol.
Quantité de matire de nitrate de potassium : 20,00 / 62 mmol.
Masse de nitrate de potassium = 20,00 / 62 x101,1 = 32,61 mg.
2.b. Proposer un mode opératoire pour cette préparation.
Peser à la balance de précision 32,61 mg de nitrate de potassium.
Dissoudre dans 100 mL d'eau distillée et verser dans une fiole jaugée de 1,00 L.
Compléter avec de l'eau distillée jusqu'au trait de jauge. Boucher et agiter pour rendre homogène.
3. Compléter l'avant dernière ligne du tableau.
4.a Rappeler la loi de Beer-Lambert.
La relation fondamentale utilisée en spectrophotométrie est présentée sous la forme :
A= log (I₀/I) = elc ( A est l'absorbance ou densité optique)
e est une caractéristique de la molécule. Plus e sera grand, plus la solution absorbe.
Absorbance et concentration étant proportionnelles, cette relation peut être utilisée pour réaliser des dosages ou des suivis cinétiques.

4.b.Tracer le graphe A = f(C). La loi de beer est-elle vérifiée ?

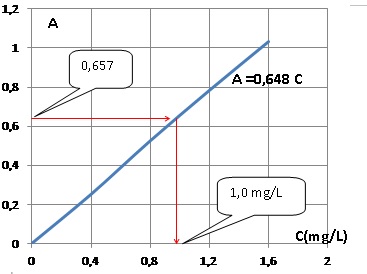
La courbe est une droite passant par l'origine : la loi de Beer est vérifiée.

5. Un échantillon d'eau de ville est traité de la même manière que la solution étalon. Déterminer la concentration massique C_x en ion nitrate dans l'eau de ville. Cette eau est-elle potable pour les ions nitrate ?
Le graphe indique 1,0 mg/L ; tenir compte de la dilution 100 / 5 = 20 ; C_x = 20 mg/L, valeur inférieure à 50. L'eau est potable pour les ions nitrate.

Les alcools.
La molécule A a pour formule semi-développée : CH₃-CH(OH) CH₂-CH₃.
1. a. Citer le nom du groupe caractéristique présent. Groupe hydroxyle OH.
1.b. Nommer A. Butan-2-ol.
1.c Donner les représentation spatiales des deux isomères du composé A. Quel nom donne-t-on à cette relation d'isomérie ?
Donner la configuration absolue de l'atome de carbone asymétrique.

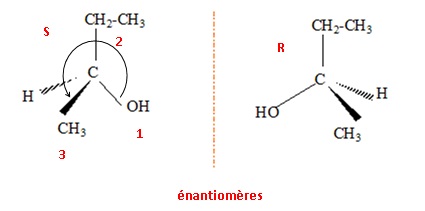
numéroter de façon décroissante chacun des quatre substituants selon son numéro atomique.
OH (1) ; CH₂CH₃ (2) ; CH₃ (3) ; H (4).
On place alors l'atome (ou le groupement) de numéro le plus élevé derrière.
On regarde dans quel sens, sens horaire ou trigonométrique, on passe du numéro 1, au 2, au 3.
- Si le sens de rotation est le sens horaire (ou anti-trigonométrique), le carbone est Rectus (R),
- Si le sens de rotation est le sens trigonométrique (ou anti-horaire), le carbone est Sinister (S).

2. On envisage la réaction d'oxydo-réduction suivante :
A --> C₄H₈O, ( noté B, cétone ) en présence de KMnO₄ acidifié (1).
2.a. Nommer B et donner sa formule semi-développée.
Butan-2-one. CH₃-C=O CH₂-CH₃.
2.b. Ecrire les demi-équations électroniques mises en jeu et en déduire l'équation de la réaction.
2 fois { MnO₄^- + 8H⁺+5 e^- = Mn²⁺ + 4H₂O } réduction
5 fois { CH₃-CH₂-CH(OH)-CH₃= CH₃-CH₂-CO-CH₃+ 2H⁺ + 2 e^- } oxydation.
2MnO₄^- + 5CH₃-CH₂-CH(OH)-CH₃+ 6H⁺ =5 CH₃-CH₂-CO-CH₃+2 Mn²⁺ +8H₂O
3. On chauffe A en milieu acide et on obtient C ( C₄H₈).
A ---> C +H2O (2)
3.a Cette réaction est-elle une addition, une substitution ou une élimination ? Justifier.
Elimination d'une molécule d'eau à partir d'un alcool. Une liaison double C= C est formée.
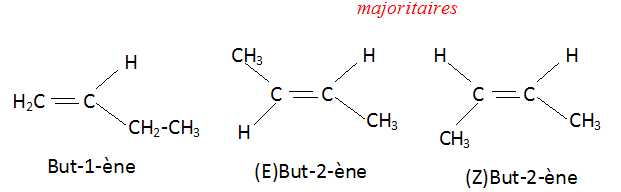
3.b. Donner les formules semi-développées des deux isomères de position C₁ et C₂ de C. Quel est celui qui est majoritaire ?
L'alcène le plus substitué se forme majoritairement.

menu