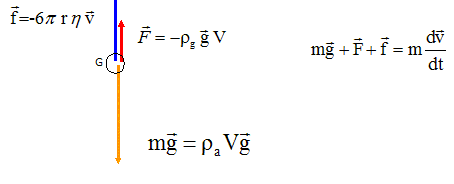Mathématiques,
Physique, chimie,
Concours TSPEI 2016.
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Exercice 1.
1. Etudier les
variations de la fonction définie de R dans R par :
f(x) =x 3 +3x 2+3x+2.
Donner le tableau de variation de f.
Dérivée f '(x) = 3x 2 +6x+3=3(x 2+2x+1)=3(x+1) 2.
f '(x) = 0 pour x = -1.
f '(x) est toujours positive ou nulle ; f (x) est croissante.
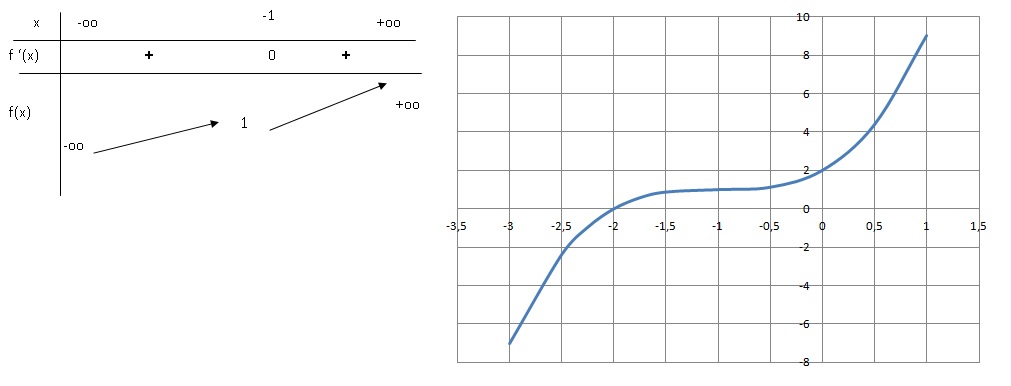 2.
2. Montrer que
l'équation x 3+3x 2+3x+2 = 0 admet une seule
solution notée a.
f(x) est continue, strictement croissante sur ]-oo ;
1[.
f(x) tend vers moins l'infini quand x tend vers -oo ; f(1) = 1.
D'après le théorème des valeurs intermédiaires, l'équation x3+3x2+3x+2
= 0 admet une seule solution dans R..
3. Montrer que si a est un nombre
entier alors |a|
divise 2.
a = -2 ; |a|
=2 ; k =1.
|a| divise 2
signifie que |a| = 2k avec k entier.
4. Calculer
f(-2).
f(-2) = (-2)3 + 3*(-2)2+3*(-2)+2 = 0.
5. x3
+3x2+3x+2 = (x+2)(bx2+ax +1)=bx3 +ax2+x+2bx2+2ax+2.
par suite b =1 et a = 1.
x3 +3x2+3x+2 = (x+2)(x2+x
+1) =0 ; a = -2.
6. Résoudre dans C
l'équation z3
+3z2+3z+2 =0. Donner pour chaque solution le module et
l'argument.
Une solution réelle z = -2. Module |z| = 2 ; argument : 0.
x2+x +1 =0.
Discriminant D = 12
-4 = -3 = 3 i2.
z1 =(-1 + i 3½) / 2 ; |z1| = ((-1)2
+ 3)½ / 2= 1.
z1 / |z1| = -1/2 +3½/2 = cos q1 +i sin q1 ; q1 =2 p/3.
z2 =(-1 - i 3½)
/ 2. |z2| = ((-1)2
+ 3)½ / 2= 1.
z2 / |z2| = -1/2 -3½/2 = cos q2 +i sin q2 ; q2 = -2p/3.
|
| .
. |
....
...
|
Exercice 2.
Un médecin qui dispose d'un répondeur est contacté par ses patients sur
appel téléphonique. Quand le médecin est absent, il branche
systématiquement son répondeur. Quand il est présent, il branche son
répondeur une fois sur trois. Quand un patient téléphone, il a 4
chances sur 5 d'obtenir le répondeur et une chance sur cinq d'obtenir
le médecin.
Un patient téléphone au médecin.
On note R l'événement " le patient obtient le répondeur".
On note A l'événement " le médecin est absent".
On note x la probabilité que le médecin
soit présent.
1. Traduire les
propositions figurant dans l'énoncé à l'aide de probabilité faisant
intervenir les événements A et R.
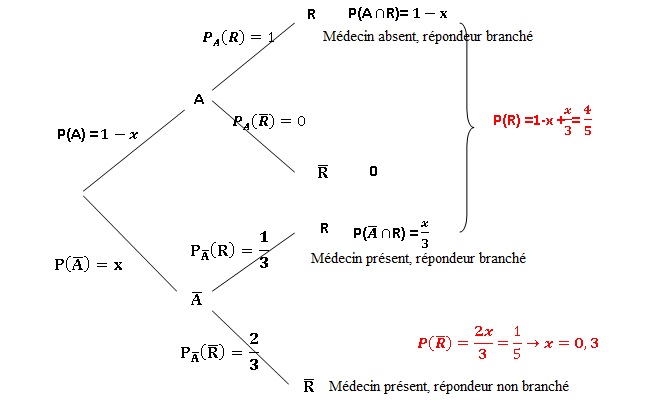
2.Exprimer
en fonction de x, P(R n A) et P (R n contraire de A).
3. En déduire la
valeur de x. Interpréter le résultat obtenu.
3 fois sur 10, lors d'un appel, le médecin est présent.
4. Un patient téléphone et obtient
le répondeur. Déterminer la probabilité que le médecin soit présent.
PR(contraire de A) =P(R n contraire de A) / P(R) =(x
/3) / 0,8 = 1 / 8 =0,125
5. Trois patients
appelle le médecin indépendamment les uns des autres. Quelle est la
probabilité que 2 patients sur 3 obtiennent le médecin ?
Probabilité que le patient obtienne le médecin : 2x /3 = 0,6/3 = 0,2.
Probabilité que deux patients 0btiennent le médecin : 0,2 x0,2 = 0,04.
|
|
|
Traitement
d'eaux usées .
Dans une station d'épuration, l'effluent traverse une grille qui
retient les déchets solides les plus volumineux ( dégrillage) puis est
placé dans un bac de prétraitement où il subit une opération de
sédimentation. On modélise les particules par une sphère homogène de
masse volumique ra
et de rayon r. On note d = rs
/rg
avec rg
masse volumique du fluide. La particule est soumise au cours de son
mouvement à une force de traînée f.
1. Effectuer le
bilan des forces appliquées à la particule. ( V = 4 / 3 p r3 volume de la
particule).
La bille
est soumise à son poids, à la poussée d'Archimède et à une force de
frottement fluide.
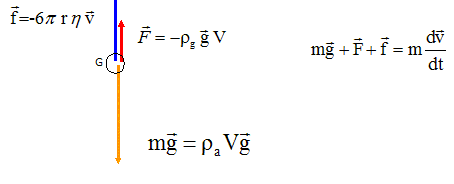
2. Etablir l'équation différentielle
régissant la vitesse v de la particule.
Projeter la relation vectorielle précédente sur un axe vertical orienté
vers le bas.
raVg-rgVg -6prnv = raV dv/dt =raV v '.
3. Déterminer la
vitesse limite vl de la particule en fonction de r, d, g et
de la viscosité cinématique n
= h / rg.
dvl / dt = 0 ; raVg-rgVg =6p r n vl.
(d-1)Vg =6p
r n vl.
vl =(d-1)Vg /(6pr n)=2 / 9 (d-1)g r2
/ n.
4.
A quelle condition y aura-t-il sédimentation ou remontée en surface ?
Si d > 1, il y a sédimentation ; si d <1 , il y a remontée.
5. On suppose que
la vitesse limite est atteinte très rapidement. Pour les particules
proposées ci-dessous, calculer la vitesse limite et le temps nécessaire
pour parcourir un distance h = 2,0 m : g = 9,8 m s-2 ; n = 1,0 10-6 m2
s-1 ; d = 2,65.
Sable fin : r = 100 µm.
Vitesse limite : 2 / 9 (d-1)g r2
/ n =2 / 9 x1,65 x9,8 x10-8 /10-6 ~0,036 m s-1.
Durée : 2 / 0,036 ~56 s.
Colloïde r = 0,10 µm.
Vitesse limite : 2 / 9 (d-1)g r2
/ n =2 / 9 x1,65 x9,8 x10-14 /10-6 ~3,6 10-8 m s-1.
Durée : 2 / (3,6 10-8) ~5,6 107 s.
6.
Le temps de chute ne peut pas dépasser 2 heures afin d'éviter la
remontée des sédiments. En déduire la valeur minimale de r.
vl = 2 / 7200 = 2,777 10-4 m s-1.
r2=9vln/(2(d-1)g) =9 x2,777 10-4 x10-6 /(2x1,65x9,8) =7,73 10-11 : r =8,8 10-6 m = 8,8 µm.
|
|
|
|
Machine frigorifique.
Un fluide réfrigérant décrit un cycle ditherme réversible entre une source chaude de température Tc, et une source froide de température Tf. On note Qc et Qf
les transferts thermiques échangées par le fluide avec respectivement
la source chaude et la source froide, et W le travail échangé au cours
du cycle.
1. Dans le cas
d'une machine frigorifique, quel milieu ( extérieur ou intérieur du
réfrigérateur ) constitue la source chaude ? La source froide ?
Le rôle d'une machine frigorifique est d'extraire de la chaleur à une source froide.
Il faut refroidir l'intérieur du réfrigérateur qui constitue la source froide.
L'extérieur gagne de la chaleur, il constitue la source chaudee.
2. Quels sont les signes de Qc, Qf et W ? Justifier.
Au cours d'un cycle le fluide reçoit le travail W compté positivement, prend la chaleur Qf à la source froide (aliments à refroidir) et céde la chaleur Qc à l'extérieur, source chaude.
Qf reçue par le fluide est comptée positivement.
Qc cédée par le fluide est comptée négativement.
3. A partir du premier principe de la thermodynamique, exprimer une relation entre W, Qc et Qf.
Au cours du cycle W +Qc+Qf = 0.
4. Définir l'efficacité h de la machine frigorifique puis l'exprimer en fonction de Qc et Qf.
Efficacité : énergie enlevée à la source foide divisée par le travail investi.
h = Qf / W = Qf / (-Qc-Qf) = -1/(Qc /Qf +1)
5. A partir du second principe, établir une relation entre Qc, Qf, Tc et Tf.
Au cours du cycle réversible, Qc / Tc +Qf / Tf = 0.
6. En déduire que pour le réfrigérateur, h = Tf / (Tc-Tf).
Qc /Qf = -Tc / Tf.
h =-1 / ( -Tc / Tf +1) = -Tf / (-Tc+Tf) = Tf / (Tc-Tf).
7. Calculer h pour Tc = 300 K et Tf = 280 K.
h = 280 / 20 = 14.
|
Autour de l'énergie.
Un accélérateur de particules fonctionne 270 jours par an, et ce 24 h sur 24 h. Sa puissance moyyenne consommée est P = 120 MW.
1. Déterminer l'énergie Ea consommée annuellement en joule.
Ea = P t = 120 106 x(270 x24 x3600)~2,8 1015 J.
2. Le faisceau de particules est constitué de N = 3,01 1014 protons ayant chacun une énergie E0 = 7,00 TeV. Calculer l'énergie E du faisceau en eV puis en joule.
E0 = 7,00 1012 eV ; E = N E0 = 3,01 1014 x7,00 1012 = 2,107 1027 eV soit 2,107 1027 x1,60 10-19 = 3,37 108 J.
3. A quelle vitesse v cette énergie correspondrait-elle pour un train de masse m = 680 t ?
½mv2 = E ; v = (2E / m)½ = (2 x3,37 108 / (680 103))½ ~31,5 m s-1 ou 31,5 x3,6 ~113 km /h.
4. Cette énergie permettrait-elle d'entrainer la fusion d'une masse mcu = 500 kg de cuivre initialement à la température Ti = 84°C ?
Capacité thermique massique du cuivre C = 400 J K-1 kg-1. Température de fusion du cuivre Tfusion= 1084°C.
E = mCu C(Tf-Ti) ; Tf=Ti+E /(mCu C) = 84 +3,37 108 /(500 x400)=84+1685.
Tf supérieur à Tfusion : le cuivre fond.
Hydrocarbures.
Le tableau ci-dessous donne la composition centésimale massique du
mélange constitué de composés à 4 atomes de carbone obtnu par ceaquage
catalytique du pétrole.
Produit
|
% massique
|
2-méthylpropène C4H8 (CH3)2C=CH2
|
15
|
but-1-ène C4H8 CH3-CH2-CH=CH2
|
12
|
| (Z) but-2-ène C4H8 |
12
|
| (E) but-2-ène C4H8 |
11
|
| butane C4H10 CH3-CH2-CH2-CH3 |
13
|
| 2-méthylpropane C4H10 (CH3)2CH-CH3 |
37
|
1. Donner la formule brute et la formule semi-développée des produits obtenus.
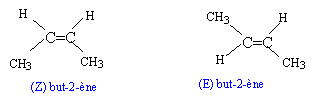
2. Quels sont les produits isomères de constitution ?
Les isomères de constitution ont même formule brute mais diffèrent par l'enchaînement de atomes.
D'une part : 2-méthylpropène, but-1-ène, (Z) but-2-ène, (E)but-1-ène.
D'autre part : butane, 2-méthylpropane.
3. Que peut-on dire du (Z) but-2-ène et du (E) but-2-ène ?
Ce sont des diastéréoisomères qui ne sont pas énantiomères.
4. Comment s'appelle le procédé permettant de séparer le gazole du pétrole ?
Raffinage, distillation fractionnée du pétrole.
Aluminothermie.
La réaction entre l'oxyde de fer (Fe2O3) et l'aluminium donne du fer et de l'oxyde d'aluminium Al2O3. La réaction étant exothermique, le fer obtenu est à l'état liquide. Ce procédé permet de souder les rails de chemin de fer.
1. Ecrire l'équation de la réaction.
2Al(s) + Fe2O3(s) --> 2Fe(l) + Al2O3(s).
2. L'élément fer est-il oxydé ou réduit ? Justifier.
Le nombre d'oxydation du fer passe de zéro dans le fer à +III dans Fe2O3. Le fer est oxydé.
3. Sachant que la réaction est exothermique, expliquer pourquoi le fer est liquide.
La chaleur dégagée par la réaction sert à chauffer les produits. La
température de fusion du fer est très inférieure à celle de l'alumine
qui reste solide.
4. Le rendement de la réaction est de 70 %.
4a. Quelle masse de fer peut-on obtenir à partir de 100 kg d'oxyde de fer (III) ? Quelle est la masse d'aluminium utilisée ?
Quantité de matière d'oxyde de fer (III) = masse d'oxyde / masse molaire de l'oxyde de fer = 100 103 / (2 x56 +3x16) = 625 mol.
Quantité de matière de fer : 2 x625 = 1250 mol.
Masse de fer : 1250x56 = 7,0 104 g = 70 kg
Tenir compte du rendement : 70 x0,7 = 49 kg.
Quantité de matière d'aluminium : 1250 mol.
Masse d'aluminium : 1250 x27 = 3,375 104 g ou environ 34 kg.
4b. La soudure de
deux rails de 18 m chacun nécessite 1,5 kg de fer. Quelle est la masse
d'oxyde de fer (III) nécessaire pour souder 900 m de rails ?
900 /18 =50 soit 49 soudures.
Masse de fer 1,5 x49 = 73,5 kg.
Quantité de matière de fer : 73,5 103 /56~1,31 103 mol.
Quantité de matière d'oxyde de fer : 1,31 103 / 2 ~656 mol.
Masse d'oxyde de fer (III) : 656 x(2x56+48) ~ 1,05 105 g ou 105 kg.
Tenir compte du rendement : 105 / 0,70 ~150 kg.
Dosage d'une solution d'acide chlorhydrique.
On dispose d'un flacon d'acide chlorhydrique concentré où l'étiquette
porte l'indication 33 % minimum en masse d'acide chlorhydrique.
On appelle S0 cette solution de concentration C0.
Etape 1 : on dilue 1000 fois S0. On obtient une solution S1 de concentration C1.
Etape 2. On prélève V1 = 100,0 mL de S1 que l'on dose par conductimétrie à l'aide d'une solution titrante d'hydroxyde de sodium de concentration Cb = 0,100 mol / L.
1. Ecrire l'équation de la réaction acido-basique.
HO-aq + H3O+aq ---> 2H2O(l).
2. Déterminer graphiquement le volume VE versé à l'équivalence.
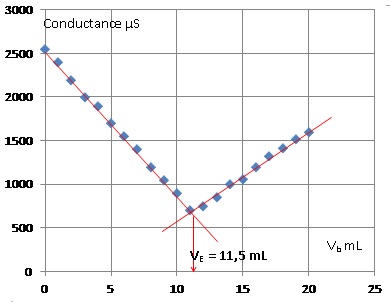
3. Déterminer C0.
A l'équivalence : CbVE = V1C1 ; C1 = 0,100 x11,5 / 100,0 = 1,15 10-2 mol/L.
C0 = 1000 x1,15 10-2 = 11,5 mol/L.
4. Calculer la masse d'acide dans un litre de solution S0. M(HCl) = 36,5 g /mol.
11,5 x36,5 ~4,2 102 g.
La solution S0 a une masse volumique r0 = 1160 g /L.
5. Quelle est la masse de 1 L de solution S0 ?
1,16 kg.
6. Calculer le pourcentage massique de la solution S0 et conclure.
420 /1160 ~0,36 ( 36 %).
Ecart relatif (36-33) / 33 ~9,1 10-2 ( environ 9%).
L'indication portée par l'étiquette ( >33%) est correcte mais reste approximative.
On donne le graphe obtenu en simulant un dosage pHmétrique.
7. Déterminer le pH à l'équivalence.
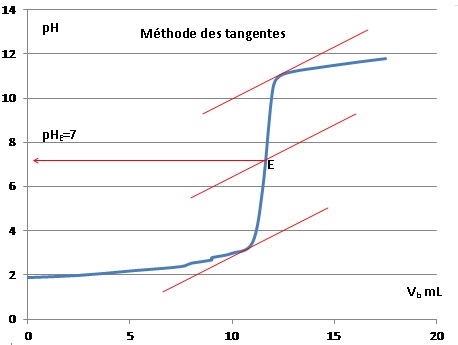
8. Quel est l'indicateur coloré le plus approprié ?
La zone de virage de l'indicateur coloré doit contenir le pH du point
équivalent. Donc le bleu de bromothymol est le plus approprié.
|
|